系列综述：
💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于【CodeTopHot200】进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证，所有代码均优先参考最佳性能。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

---

---

😊点此到文末惊喜↩︎

基础知识

二叉树广度优先遍历*

递归算法

1. 非重点

   // 递归参数，如果需要修改要进行引用传递
   void traversal(TreeNode* cur, vector<vector<int>>& result, int depth) {
   	// 递归出口
       if (cur == nullptr) return;
       // 递归体
       if (result.size() == depth) // 扩容
       	result.push_back(vector<int>());// 原地构建数组
       result[depth].push_back(cur->val);// 顺序压入对应深度的数组中
       order(cur->left, result, depth + 1);
       order(cur->right, result, depth + 1);
   }
   vector<vector<int>> levelOrder(TreeNode* root) {
   	// 初始化：一般为递归形参
       vector<vector<int>> result;
       int depth = 0;
       // 递归调用
       traversal(root, result, depth);
       // 返回结果
       return result;
   }
   

非递归算法

1. 重点

   vector<vector<int>> levelOrder(TreeNode* root) {
       vector<vector<int>> res;	// 结果容器
       queue<TreeNode*> que;		// 队列
       if (root != nullptr) que.push(root);// 根非空入队
       while (!que.empty()) {
           vector<int> vec;		// 每层结果
           int size = que.size();	// 记录当前层结点数量
           for (int i = 0; i < size; ++i) {
           	// 先记录后修改
               TreeNode *node = que.front();
               que.pop();
               // 按序压入每个结点的左右孩子
               if (node->left) que.push(node->left);
               if (node->right) que.push(node->right);
   			// 每个结点的处理
               vec.push_back(node->val);
           }
           // 每层结点的处理
           res.emplace_back(vec);
   
       } 
       return res;
   }
   

相关题目

199. 二叉树的右视图

1. 题目
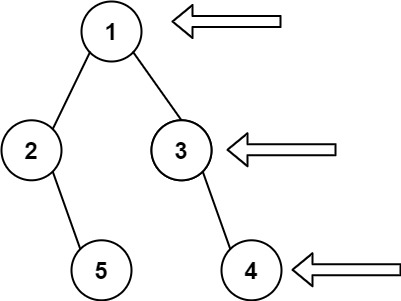
   • 给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
     

vector<int> rightSideView(TreeNode* root) {
    queue<TreeNode*> que;
    if (root != NULL) que.push(root);
    vector<int> result;
    while (!que.empty()) {
        int size = que.size();
        for (int i = 0; i < size; i++) {
            TreeNode* node = que.front();
            que.pop();
            // 将每一层的最后元素放入result数组中
            if (i == (size - 1)) result.push_back(node->val);
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
    }
    return result;
}

104. 二叉树的最大深度

1. 题目
   • 给定一个二叉树 root ，返回其最大深度。
   • 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

// 递归方式(后序遍历的应用模板)
int maxDepth(TreeNode* root) {
    auto self = [&](auto &&self, TreeNode *root)->int{
        if (root == nullptr) return 0;
        int max_left = self(self, root->left);
        int max_right = self(self, root->right);
        return max(max_left, max_right) + 1;
    };
    return self(self, root);
}

// 非递归方式
int maxDepth(TreeNode *root) {
    int depth = 0;           // 结果
    queue<TreeNode*> que;    // 队列
    if (root != nullptr)que.push(root);
    while (!que.empty()) {
        // 层次遍历
        int size = que.size();
        for (int i = 0; i < size; ++i) {
        TreeNode *node = que.front();
        que.pop();
        if (node->left) que.push(node->left);
        if (node->right) que.push(node->right);
        }
        // 层数+1
        ++depth;
    } 
    return depth;
}

111. 二叉树的最小深度

1. 核心思路
   • 层次遍历中，一直记录深度。直到返回第一个左右孩子均为空时的depth
2. 递归法
   • 分别对二叉树的五种形态进行讨论

   int minDepth(TreeNode* root) {
   	// 空二叉树
       if (root == NULL) return 0;
       // 只有左子树
       if (root->left != NULL && root->right == NULL) {
           return 1 + minDepth(root->left);
       }
       // 只有右子树
       if (root->left == NULL && root->right != NULL) {
           return 1 + minDepth(root->right);
       }
       // 左右子树都非空
       return 1 + min(minDepth(root->left), minDepth(root->right));
   }
   

3. 非递归法
   • 层次遍历中：找到第一个左右孩子均为空的，即为最小深度

   int minDepth(TreeNode* root) {
       if (root == NULL) return 0;
       int depth = 0;
       queue<TreeNode*> que;
       que.push(root);
       while(!que.empty()) {
           int size = que.size();
           depth++; // 记录最小深度
           for (int i = 0; i < size; i++) {
               TreeNode* node = que.front();
               que.pop();
               if (!node->left && !node->right) { // 第一个左右孩子均空，为最小深度
                   return depth;
               if (node->left) que.push(node->left);
               if (node->right) que.push(node->right);
               }
           }
       }
       return depth;
   }
   

求二叉树最左下的叶子

1. 题目
   • 给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。
2. 思路
   • 使用层次遍历：每次记录第一个结点的值，最后就是最左下的结点

int findBottomLeftValue(TreeNode* root) {
   TreeNode *res = nullptr;
    queue<TreeNode*> que;
    if (root != nullptr) que.push(root);
    while (!que.empty()) {
        int size = que.size();
        for (int i = 0; i < size; ++i) {
            TreeNode *node = que.front();
            que.pop();
            if (i == 0) res = node; // 每次记录第一个结点
            if (node->left) que.push(node->left);
            if (node->right) que.push(node->right);
        }
    }
    return res->val;

}

---

少年，我观你骨骼清奇，颖悟绝伦，必成人中龙凤。 不如点赞·收藏·关注一波

---

🚩点此跳转到首行↩︎

参考博客

1. 「代码随想录」47. 全排列 II:【彻底理解排列中的去重问题】详解
2. codetop