文章目录
- 一、联合体
- 1. 联合体类型的声明和创建
- 2. 联合体的特点
- 3. 联合体大小的计算
- 4.总结
- 二、枚举
- 1. 枚举类型的声明
- 2. 枚举类型的优点
- 3. 枚举类型的使用
一、联合体
(1) 像结构体⼀样,联合体也是由一个或者多个成员构成,这些成员可以不同的类型。
(2)但是编译器只为最大的成员分配足够的内存空间。联合体的特点是所有成员共用同一块内存空间。所以联合体也叫:共用体。
(3) 给联合体其中⼀个成员赋值,其他成员的值也跟着变化。
1. 联合体类型的声明和创建
关键字:union
声明:
#include <stdio.h>
//联合类型的声明
union Un// 类型名
{
char c;//成员
int i;
};
int main()
{
union Un s = {0};//创建
return 0;
}
2. 联合体的特点
联合的成员是共用同⼀块内存空间的,这样⼀个联合变量的大小,至少是最大成员的大小(因为联合至少得有能力保存最大的那个成员)。
//代码1
#include <stdio.h>
//联合类型的声明
union Un
{
char c;
int i;
};
int main()
{
//联合变量的定义
union Un un = {0};
// 下⾯输出的结果是⼀样的吗?
printf("%p\n", &(un.i));
printf("%p\n", &(un.c));
printf("%p\n", &un);
return 0;
}
运行结果:
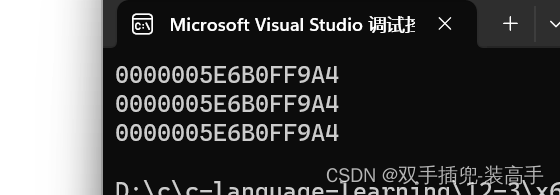
它们的地址都是一样的,说明它们共用一块空间
我们再来举一个例子
union Un
{
char c;
int i;
};
int main()
{
//联合变量的定义
union Un un = { 0 };
un.i = 0x11223344;
printf("%x\n", un.i);
un.c = 0x55;
printf("%x\n", un.i);
return 0;
}
运行结果:
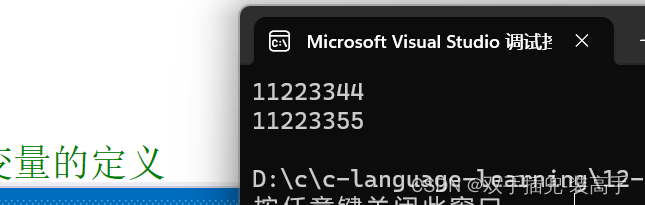
为什么结果不一样呢?
是因为它们共用一块空间,当 c 使用时就会改变 i 的值
内存布局:
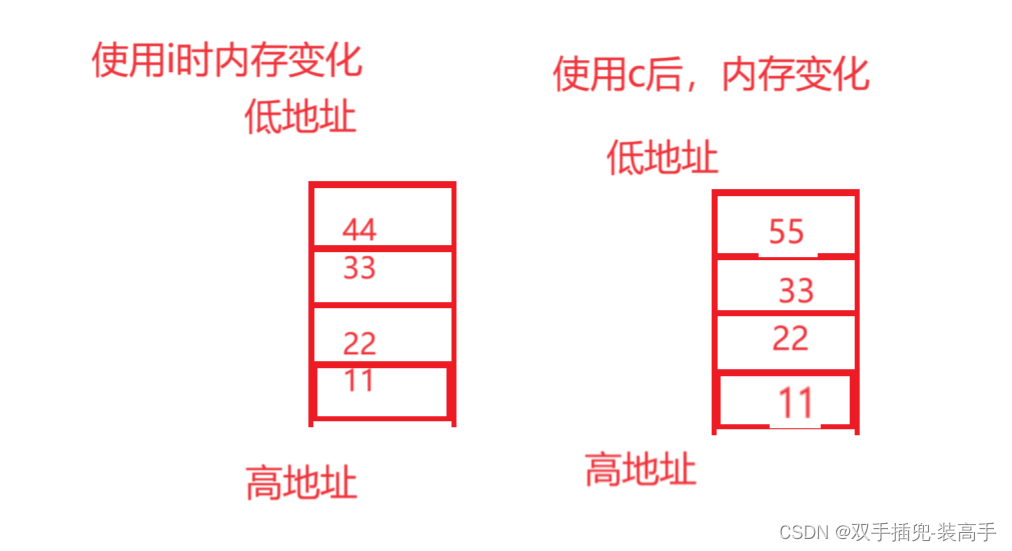
3. 联合体大小的计算
联合的大小至少是最大成员的大小。
当最大成员大小不是最大对齐数的整数倍的时候,就要对齐到最大对齐数的整数倍。
如:
#include <stdio.h>
union Un1
{
char c[5];
int i;
};
union Un2
{
short c[7];
int i;
};
int main()
{
//下⾯输出的结果是什么?
printf("%d\n", sizeof(union Un1));
printf("%d\n", sizeof(union Un2));
return 0;
}
运行结果:
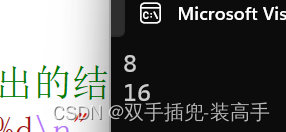
当遇到数组是我们只看类型如char c[5];->我们只看char的对齐数,char的对齐数为1
第一个输出结果
该类型的最大对齐数为4(int)
数组的大小为7,我们要保证它的大小,只能是最大对齐数的倍数,所以是8
第二个输出结果同理
4.总结
(1)使用联合体是可以节省空间的
(2)使用联合体的一个成员时就不要使用其他成员(因为其他成员的值会发生变化)
二、枚举
1. 枚举类型的声明
关键字:enum
枚举顾名思义就是⼀⼀列举。
把可能的取值⼀⼀列举。
比如我们现实生活中: ⼀周的星期⼀到星期日是有限的7天,可以⼀⼀列举
性别有:男、女、保密,也可以⼀⼀列举
月份有12个月,也可以⼀⼀列举
三原色,也是可以意义列举 这些数据的表示就可以使用枚举了。
如:
enum Day//星期
{
Mon,
Tues,
Wed,
Thur,
Fri,
Sat,
Sun
};
enum Sex//性别
{
MALE,
FEMALE,
SECRET
};
enum Color//颜⾊
{
RED,
GREEN,
BLUE
};
以上定义的 enum Day , enum Sex , enum Color 都是枚举类型。
{}中的内容是枚举类型的可能取值,也叫 枚举常量 。
这些可能取值都是有值的,默认从0开始,依次递增1,当然在声明枚举类型的时候也可以赋初值。
如:
enum Color//颜⾊
{
RED=2,
GREEN=4,
BLUE=8
};
2. 枚举类型的优点
为什么使用枚举? 我们可以使用 #define 定义常量,为什么非要使用枚举? 枚举的优点:
- 增加代码的可读性和可维护性
- 和#define定义的标识符⽐较枚举有类型检查,更加严谨。
- 便于调试,预处理阶段会删除 #define 定义的符号
- 使用方便,⼀次可以定义多个常量
- 枚举常量是遵循作用域规则的,枚举声明在函数内,只能在函数内使用
3. 枚举类型的使用
enum Color//颜⾊
{
RED=1,
GREEN=2,
BLUE=4
};
enum Color clr = GREEN;//使⽤枚举常量给枚举变量赋值
那是否可以拿整数给枚举变量赋值呢?在C语言中是可以的,但是在C++是不⾏的,C++的类型检查比较严格。
以上就是我的分享了,如果有什么错误,欢迎在评论区留言。
最后,谢谢大家的观看!