文章目录
- 面试题 08.01. 三步问题
- 题干:
- 算法原理:
- 1、状态表示
- 2、状态转移方程
- 3、初始化
- 4、填表顺序
- 5、返回值
- 代码:
- 209. 长度最小的子数组
- 题干:
- 算法原理:
- 1、暴力枚举出所有的子数组的和
- 2、利用单调性,使用“同向双指正”来优化
- 代码:
- 3. 无重复字符的最长子串
- 题干:
- 算法原理:
- 1、暴力枚举 + 哈希表(判断字符是否重复出现)
- 2、利用规律,使用“滑动窗口”来解决问题
- 代码:
面试题 08.01. 三步问题

原题链接
题干:
小孩可以一次上 1阶 2阶 3阶
刚开始看题目可能不太清楚
我们画图看一看
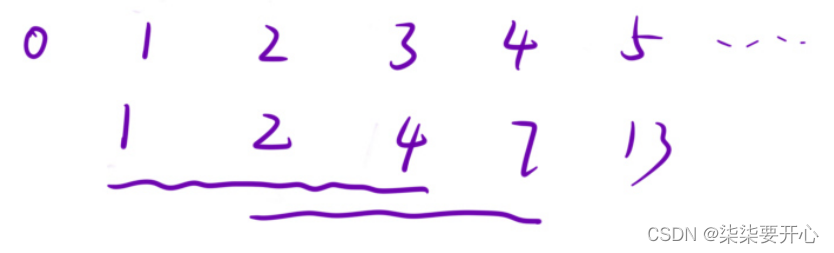
如果是一节台阶,只有一种情况
如果是两节台阶,从0到1有一种,经过1到2有一种,所以是两种
如果是三节台阶,从0到3有一种,经过1到3有一种,经过2到3有一种,所以是四种
如果是四阶台阶,经过1到4有一种,经过2到4有两种,经过3到4有四种,所以一共有七种
…
以此类推
从第三个以后,每个台阶数都是前面的三个数之和
和前面的泰波那契数很像
算法原理:
1、状态表示
dp[i] 表示:到达 i 位置时,一共有多少种方法
2、状态转移方程
以 i 位置的状态,最近的一步,来划分问题
对于 i 来说,可以是 i - 1 走一步,i - 2 走两步,i - 3 走三步
dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]
3、初始化
dq[1] = 1;
dp[2] = 2;
dp[3] = 4;
4、填表顺序
从左向右
5、返回值
dp[n]
代码:
class Solution {
public int waysToStep(int n) {
int MOD = (int)1e9 + 7;
int[] dp = new int[n + 1];
if (n == 1 || n ==2) {
return n;
}
if (n == 3) {
return 4;
}
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for (int i = 4; i <= n; i++) {
dp[i] = ((dp [i - 1] + dp[i - 2]) % MOD + dp[i - 3]) % MOD;
}
return dp[n];
}
}
209. 长度最小的子数组

原题链接
题干:
在题目中,正整数数组中有没有一个连续子数组等于目标值,然后返回长度(最短的)
算法原理:
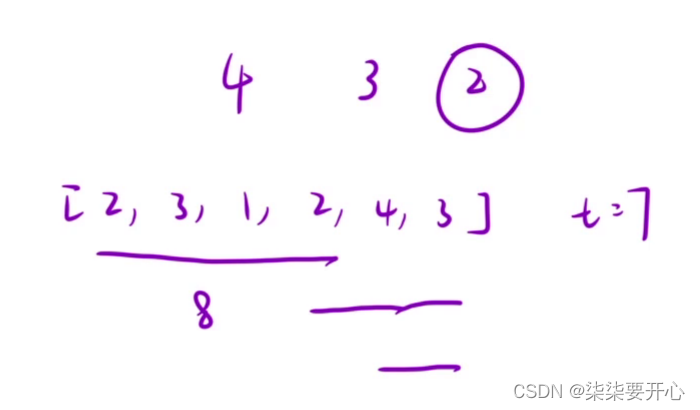
1、暴力枚举出所有的子数组的和
直接固定第一个数,从前往后来进行加法计算
时间复杂度:O(N3)
优化一:
定义一个sum,把从前往后计算的数存到sum 中
时间复杂度:O(N2)
优化二:
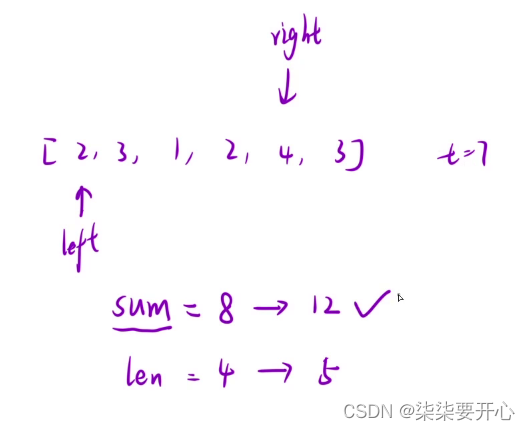
当 right 走到sum = 8的时候,往后走,虽然和在增加,但是长度也在增加,所以后面的并不是最佳答案
并且当left++ 的时候,sum 可以直接减去left 前面那个数,right 不会变
这样我们就优化到了解法二
2、利用单调性,使用“同向双指正”来优化
同向双指针被称为“滑动窗口”
在利用单调性的时候,两个指针在移动的时候都不回退,这个时候我们可以使用滑动窗口
那我们怎么使用滑动窗口呢?
- 初始化两个指针充当滑动窗口的左右端点
left = 0;
right = 0; - 进窗口
- 判断,然后决定是否出窗口
- 更新结果(不过在什么时候更新结果就题论题)
在本题中,因为要先判断 sum 是否等于目标值,先更新结果 让 len = 区间,然后再出窗口
这里的 2 和 3 是循环
为什么这里滑动窗口是对的呢?
是由于单调性的原因,在上面的一步步优化的时候就可以知道,当这个区间的和大于目标值之后,后面的值加进来肯定要大于目标值,但是这里区间长度也会增加,所以后面的值就不可能是求的值
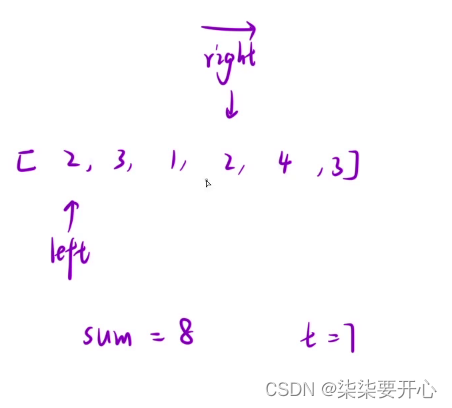
这里就是使用单调性,规避了很多没有必要的枚举行为,这里也是正确的
这里的时间复杂度O(N)
因为这个时候left 走一步,right 走一步,因此是O(N)
代码:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length;
int sum = 0;
int len = Integer.MAX_VALUE;
for (int left = 0, right = 0; right < n; right++ ) {
sum += nums[right];//进窗口
while(sum >= target) {//判断
len = Math.min(len,right - left + 1);//更新结果
sum -= nums[left++];//出窗口
}
}
return len == Integer.MAX_VALUE ? 0 : len;
}
}
3. 无重复字符的最长子串

原题数组
题干:
我们看题干,这里有了“子串”这样的概念
“子串”和“子数组”很相似,都是连续的一段
这里要找到一串子串不重复的最长子串

算法原理:
1、暴力枚举 + 哈希表(判断字符是否重复出现)
固定一个起始位置,向后拓展,直到后面的字符跟子串里面有相同的元素,统计长度
这个时候我们借用哈希表,凡是重复
时间复杂度:O(N2)
优化:
由于right 走到 后面的 a 的时候,left++,然后如果到 e 再次进行遍历,那么其实走到 a 还是重复
这个时候我们就可以直接跳过 a ,这时候 right 就不用回去了,直接++
如果是这样的话,left++ 然后 right++,都不往后退,这个时候我们就可以优化为“滑动窗口”
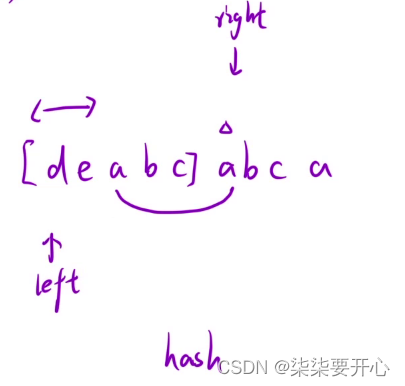
2、利用规律,使用“滑动窗口”来解决问题
- 定义 left 和 right 来充当左右端点
- 进窗口(让字符进窗口)
- 判断(当窗口内出现重复字符)
- 出窗口(要跟判断进行循环,从哈希表中删除该字符)
- 更新结果(就题论题)
在整个判断结束之后更新结果
代码:
class Solution {
public int lengthOfLongestSubstring(String ss) {
char[] s = ss.toCharArray();
int[] hash = new int[128];//用数组模拟哈希表
int left = 0;
int right = 0;
int n = ss.length();
int ret = 0;
while(right < n) {
hash[s[right]]++;//进入窗口
//这里s[right]是字符所在的下标,把它放入到hash数组对应的下标中
while(hash[s[right]] > 1) {//判断
hash[s[left++]]--;//出窗口 值归零
}
ret = Math.max(ret, right - left + 1);//更新结果
right++;//让下一个字符进入窗口
}
return ret;
}
}

![[前 5 名] 最顶级的数据恢复软件解决方案列表](https://img-blog.csdnimg.cn/direct/df0f94bc0a7748fca99dce7fcf4bad8e.png)