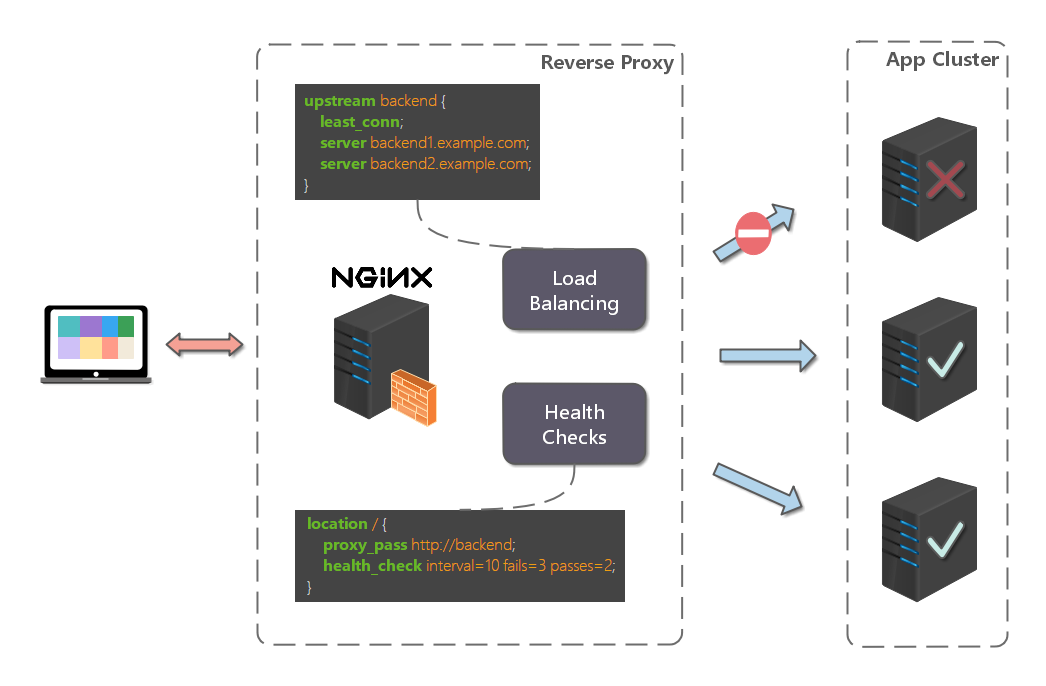
运动物体的微多普勒效应为人体动作识别提供了可能,基于雷达的居家检测具有良好的隐私保护性,且不易受环境因素影响(如光照、温度等),近年来已受到国内外学者的广泛关注。由于雷达信号的非平稳特性,通过短时傅里叶变换或者小波变换等数字信号处理方法,揭示人体运动情况的多普勒与微多普勒特征已经能够很好地显示出来,这为基于雷达地人体摔倒检测提供了理论基础。
目录
1 多普勒效应
2 微多普勒效应
3 微多普勒信号分析
1 多普勒效应
根据波动理论,当波源与观察者相互靠近或者相互远离时,观察者接收到的频率(以下简称接收频率)与波源频率不一致,这种现象叫做多普勒效应。根据波源与观察者的相对运动状态,多普勒效应可以分为以下两种情况:
(1)波源静止,观察者相对介质运动,接收频率与波源频率满足:
其中 v 为波在介质中的传播速度,v0 为观察者的径向移动速度,若观察者靠近波源则取“+”号,反之取“-”号。
(2)观察者静止,波源相对介质运动,接收频率与波源频率满足:
其中 vs 为波源的径向移动速度,若波源向观察者接近则取“-”号,反之取“+”号。
多普勒效应引起的接收频率和波源频率之差,定义为多普勒频移,即
多普勒频移可以通过对接收信号的频谱分析得到。
应用多普勒效应的雷达称为多普勒雷达(Doppler Radar),在速度相同的情况下,信号频率 越高,多普勒效应越显著。

2 微多普勒效应
在波源频率已知的情况下,运动物体速度的测量可以转换成多普勒频移的测量。或者说,多普勒效应可以用于测量运动物体的速度,例如行驶中的汽车。实际上,行驶中的汽车等物体在物理上被等效为一个刚体。
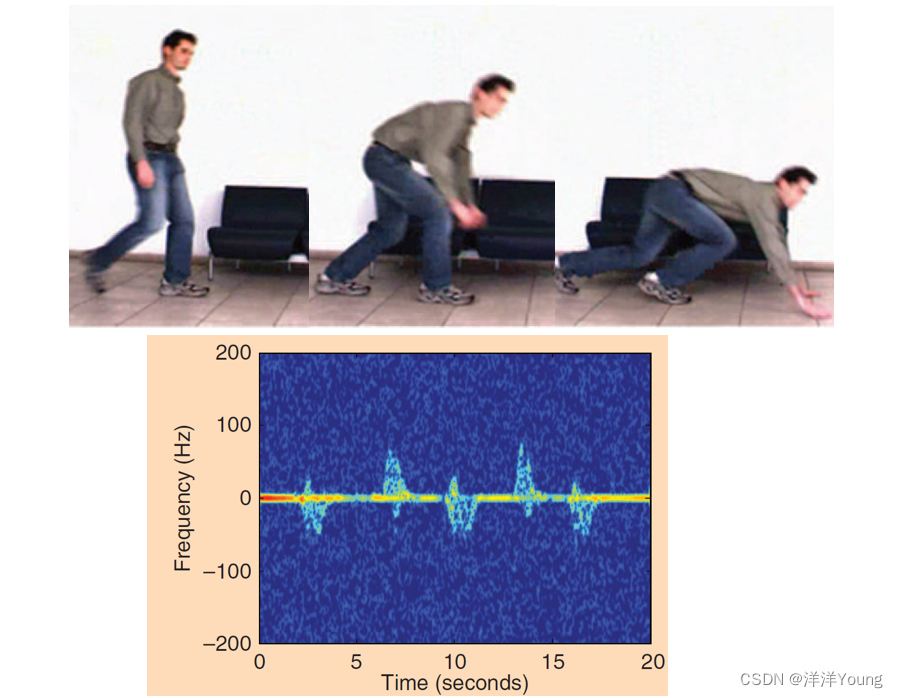
然而在基于雷达的人体摔倒检测中,人体不能被视为一个刚体。这是因为人在摔倒或者做其他动作时, 除人体躯干运动之外,通常还伴随有手臂的摆动、头部的微小晃动等运动,这些运动也会在雷达时频谱图中引入多普勒频率。这种由非刚体自身结构的振动或转动而引起的多普勒效应,被称为微多普勒效应(Micro-Doppler Effect)。
If the object or any structural component of the object has an oscillatory motion in addition to the bulk motion of the object, the oscillation will induce additional frequency modulation on the returned signal and generates side bands about the Doppler shifted frequency of the transmitted signal due to the bulk motion. The additional Doppler modulation is called the micro-Doppler effect.

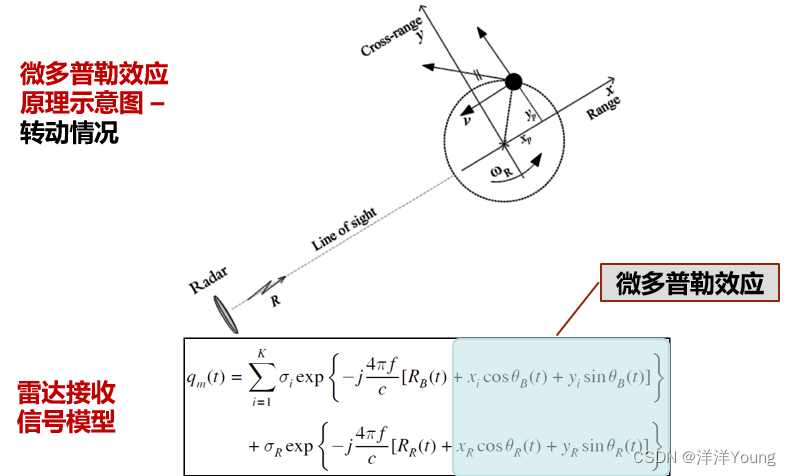
3 微多普勒信号分析
人体雷达信号的多普勒特征与微多普勒特征,分别揭示了人体躯干的运动情况和除躯干外其他部位的运动情况。然而,微多普勒信号在分析过程中,也存在着一些挑战。
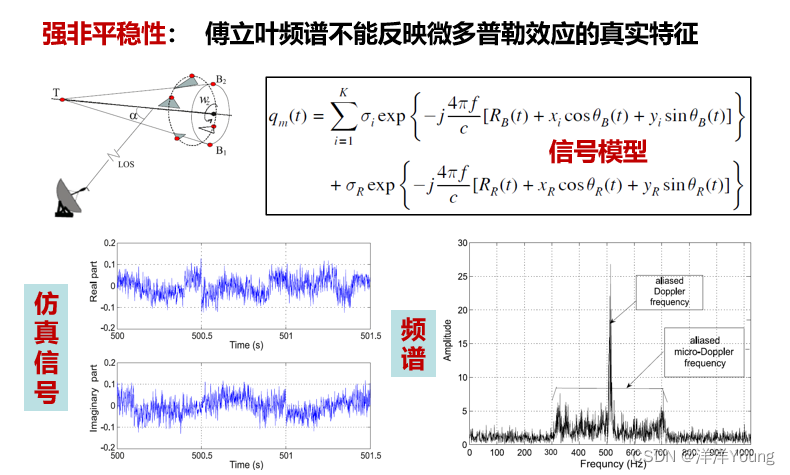
(1)强非平稳性,傅里叶频谱不能反映微多普勒效应的真实特征;
(2)多分量相互交叉,频带集中,难于分离;
(3)特征微弱,易被噪声淹没。
How to effectively decompose micro-Doppler signatures into mono-components that relate to the physical structural parts of a target and how to measure the embedded kinematic/structural information from mono-component signatures are still open issues.
对于非平稳信号,可以采用时频变换和信号分解的分析方法。时频变换方法包括短时傅里叶变换(Short Time Fourier Transform, STFT)和连续小波变换(Continuous wavelet transform, CWT).
短时傅里叶变换
连续小波变换
通过短时傅里叶变换或者小波变换等数字信号处理方法,揭示人体运动情况的多普勒特征和微多普勒特征已经能够很好地显示出来,这为基于雷达的人体摔倒检测提供了理论基础。