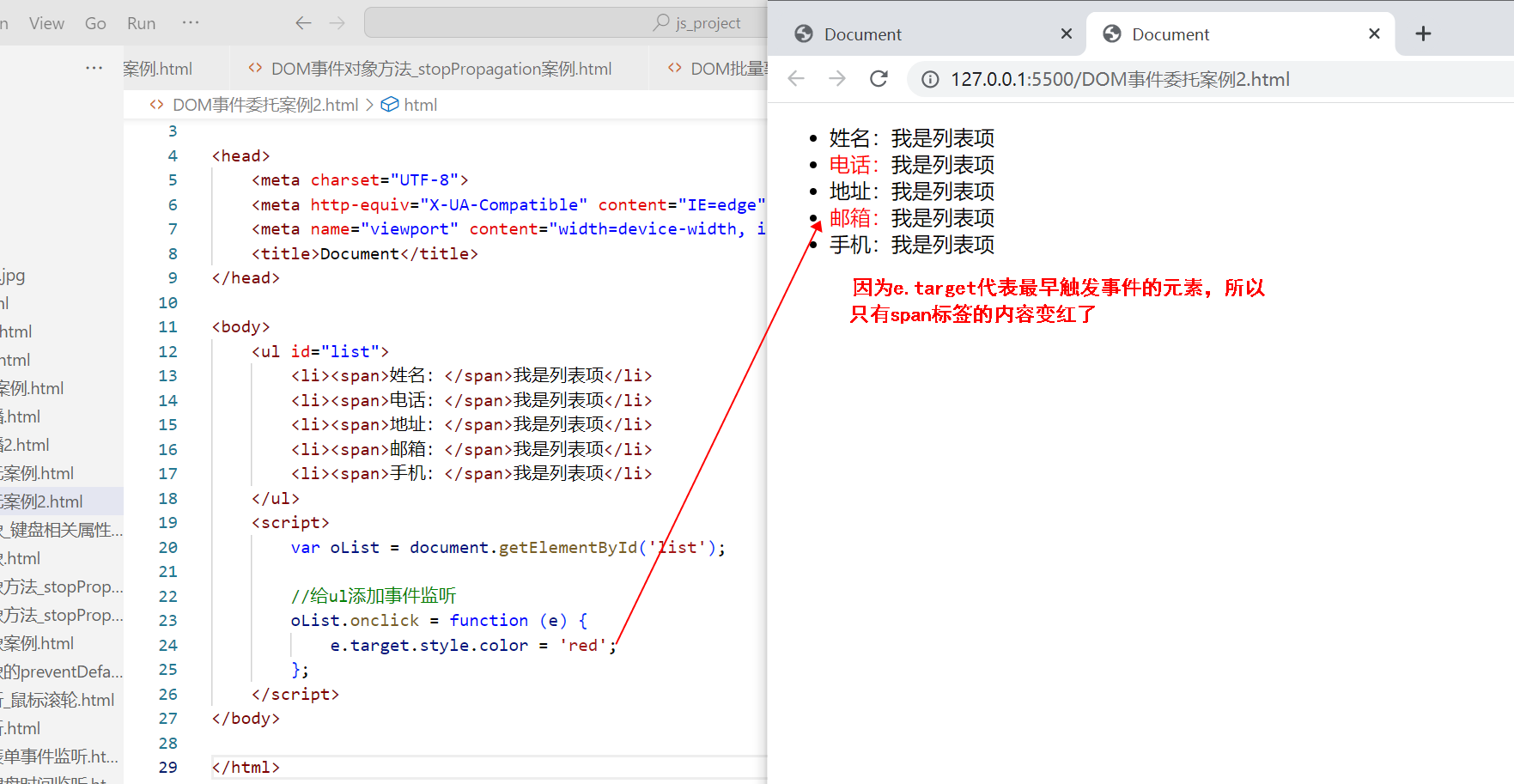
在工业应用中，光学3D表面轮廓仪超0.1nm的纵向分辨能力能够高精度测量物体的表面形貌，可用于质量控制、表面工程和纳米制造等领域。

与其它表面形貌测量方法相比，光学3D表面轮廓仪达到纳米级别的相移干涉法(PSI)和垂直扫描干涉法(VSI)，具有快速、非接触的优点。它结合了跨尺度纳米直驱技术、精密光学干涉成像技术、连续相移扫描技术三大独特技术，能够滤除光源不均匀带来的误差，以超越0.1nm的纵向分辨能力，让显微形貌分毫毕现；以优于0.1%的台阶测量重复性，让测量数据万千如一。

在半导体行业，SuperViewW系列光学3D表面轮廓仪可用于检测芯片表面缺陷和颗粒，确保产品的质量和性能，从而将不良产品阻截在市场之外；IC封装中用于测量减薄之后的厚度、晶圆的粗糙度、激光切割后的槽深槽宽，测量导线框架的粗糙度；在分立器件封装中，测量QA对打线深度，弹坑深度。

减薄工序中粗磨和细磨后的硅片表面3D图像，用表面粗糙度Sa数值大小及多次测量数值的稳定性来反馈加工质量。在生产车间强噪声环境中测量的减薄硅片，细磨硅片粗糙度集中在5nm附近，以25次测量数据计算重复性为0.046987nm，测量稳定性良好。

弹坑深度测量

在涂层表面粗糙度和厚度的研究上，可以监测纳米级结构的生长过程，为科学研究提供了更准确的测量手段。

此外，不管是从超光滑到粗糙，还是低反射率到高反射率的物体表面，光学3D表面轮廓仪都能够以优于纳米级的分辨率，自动聚焦测量工件获取2D，3D表面粗糙度、轮廓等一百余项参数。

全透明表面、漫反射表面、镜面反射表面，可测反射率：覆盖近0%~100%的表面反射率。

光学3D表面轮廓仪具有高精度、高速度和高可靠性等优点，在科学研究、质量控制、表面工程和纳米制造等领域中，发挥着举足轻重的作用。