一:判断题
1-1

答案:T
解析:c到a的最短路径是12+2=14,所以是大于10的
1-2

答案:T
一个连通分量要进行一次广度优先搜索
1-3

答案:F
解析:是存在等于顶点的个数减一的情况,比如三个顶点用两个边连接,是一个连通的,他的边数就是顶点数-1
1-4
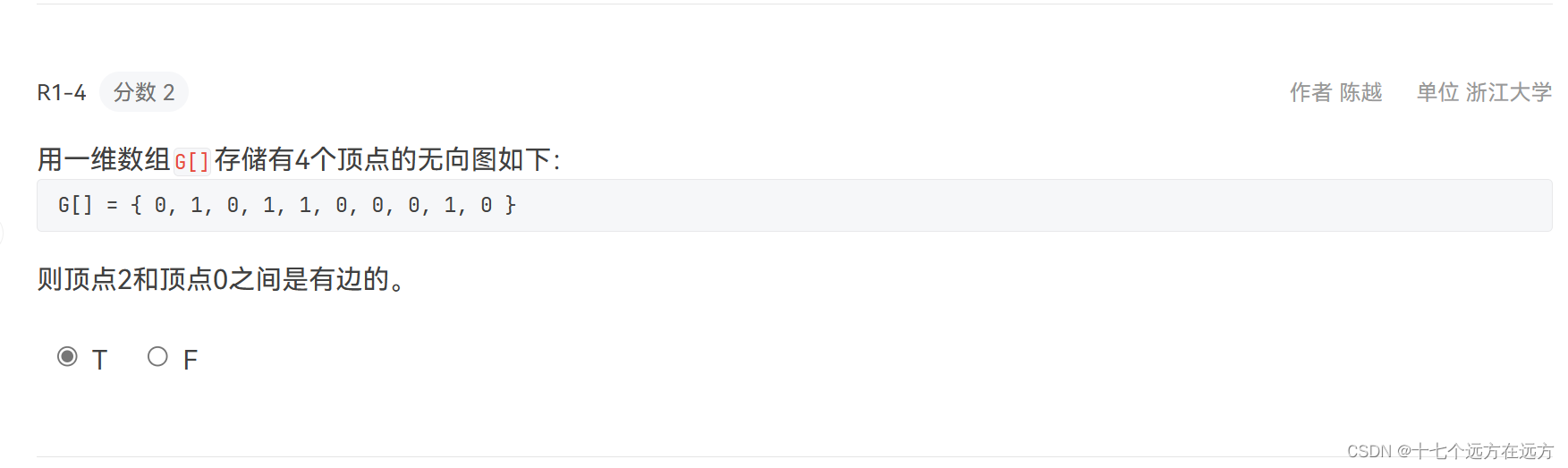
答案:T
解析:无向图的邻接矩阵沿主对角线对称;
1-5
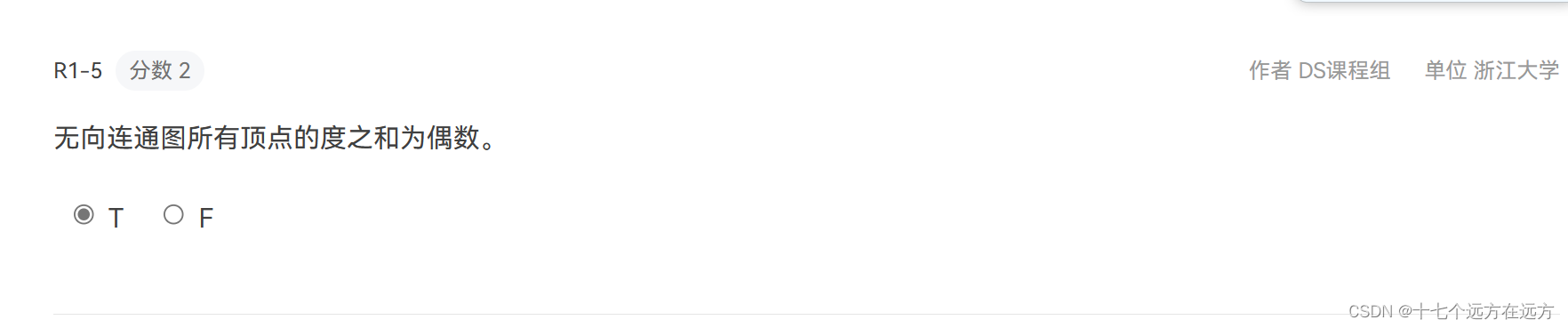
答案:T
解析:边数*2
1-6
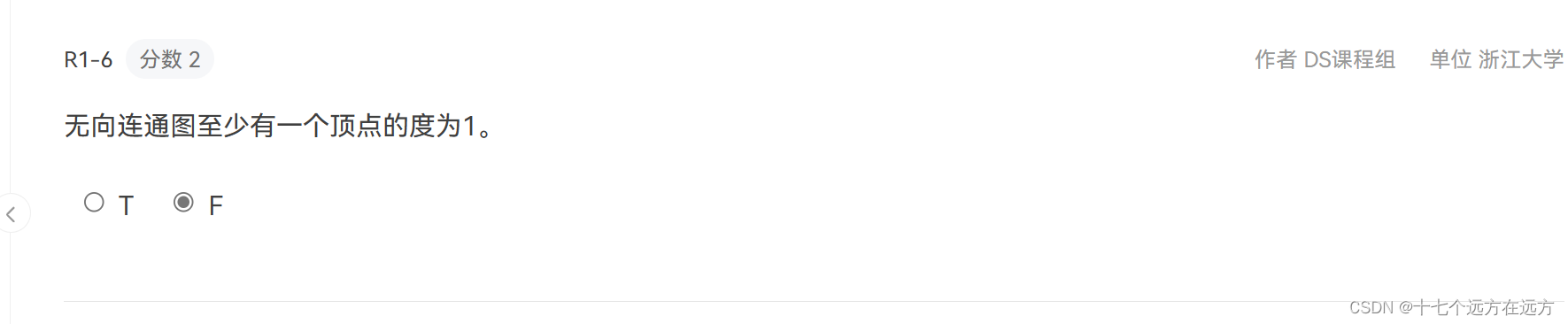
答案:F
解析:如果顶点数为3,边为3,那就是一个一个完全图,不存在度为1的顶点
1-7
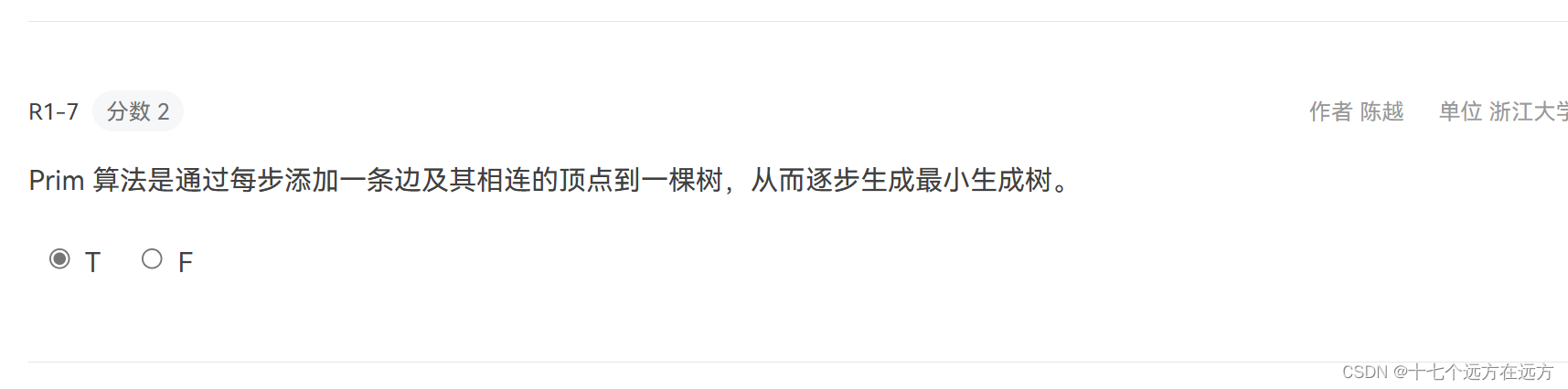
答案;T
解析:Prim算法是一种用于求解最小生成树的贪心算法。它通过每一步选择一个与当前生成树相连的顶点,并添加一条边连接该顶点和生成树中的某个顶点,从而逐步生成最小生成树。
具体来说,Prim算法的步骤如下:
初始化一个空的生成树和一个空的顶点集合。
从任意一个顶点开始,将其加入生成树,并将其相邻的边加入边集合。
从边集合中选择权重最小的边,并将其连接的顶点加入生成树和顶点集合。
重复步骤3,直到所有顶点都加入生成树。
最终生成的树就是最小生成树。
通过每一步选择权重最小的边,Prim算法保证了生成的树是最小生成树,即树中所有边的权重之和最小。
1-8

答案:T
解析:邻接矩阵是一种常见的图的表示方法,它使用一个二维数组来表示图中的顶点之间的连接关系。对于一个有n个顶点的图,邻接矩阵是一个n×n的矩阵,其中矩阵的每个元素表示两个顶点之间是否存在边。
在邻接矩阵中,如果顶点i和顶点j之间存在边,则邻接矩阵的第i行第j列和第j行第i列的元素为1;如果它们之间不存在边,则对应的元素为0。对于无向图来说,邻接矩阵是对称的。
使用邻接矩阵法存储图的优点是:
存储空间占用只与图中结点个数有关,而与边数无关。因为邻接矩阵只需要一个二维数组来表示连接关系,不需要额外的空间来存储边的信息。
可以快速判断两个顶点之间是否存在边,只需要访问邻接矩阵中的对应元素即可。
可以方便地获取顶点的度数,即与该顶点相连的边的数量。
然而,邻接矩阵法也有一些缺点,主要是在稀疏图(边数相对较少)的情况下,会浪费大量的存储空间。
1-9
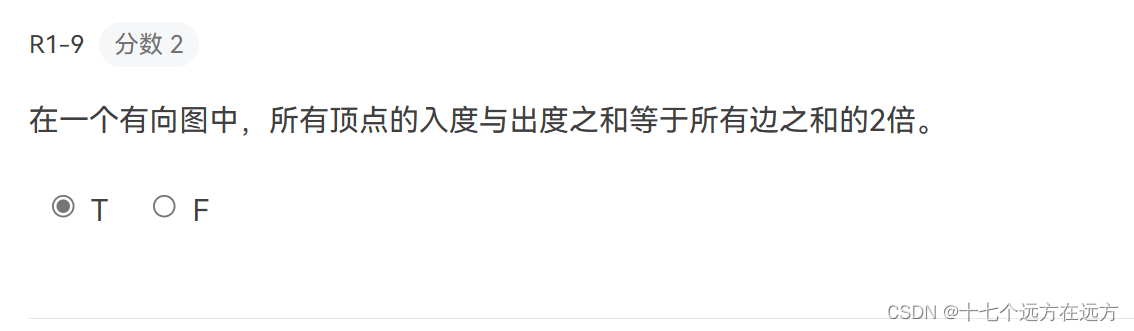
答案:T
解析:有向图的全部入度之和与出度之和想等,并且等于边数
1.所有顶点的度数之和 等于 边数的二倍。
2.所有顶点的入度之和 等于 出度之和。
3.n个顶点的有向完全图有n*(n-1)条边。
4.n个顶点的强连通图至少有n条边。
1-10

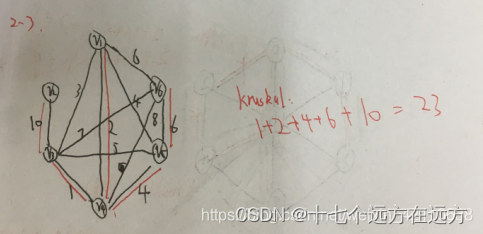
答案:F
解析:克鲁斯卡尔算法是维护一个森林,每一步把两棵树合并成一棵;
二:选择题
2-1
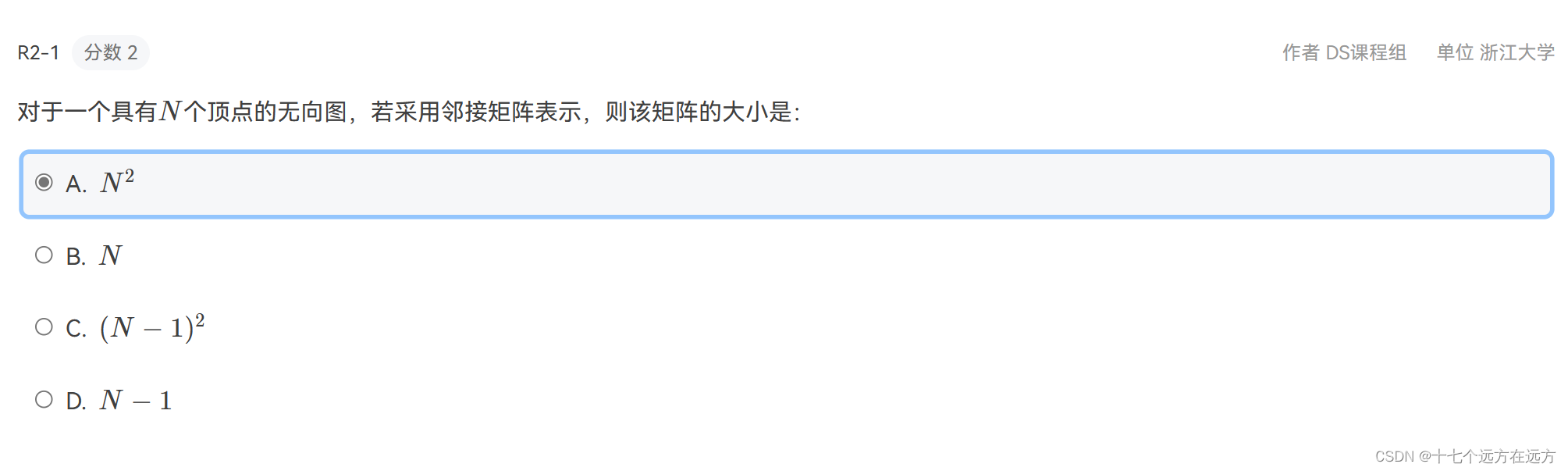
答案:A
解析:邻接矩阵是用二维数组来表示节点之间的关系,二维数组的个数就是N*N;
2-2
答案:C
解析:完全图的时候,顶点的度最大,最大是N*(N-1),所以是顶点数的N-1倍
2-3
答案:B
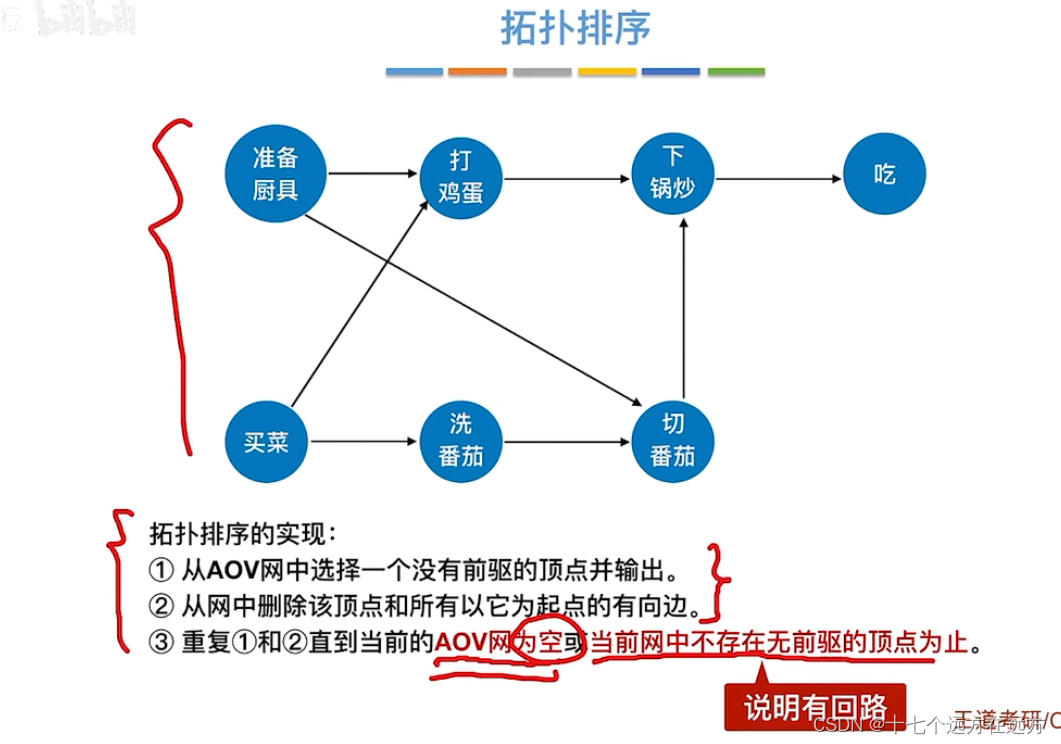
解析:图的深度遍历是适用于有向图的。深度遍历是一种通过探索图中的深层节点来遍历图的算法。它可以应用于有向图和无向图,无论图中的边是有向还是无向的。
在深度遍历中,从起始节点开始,沿着一条路径尽可能深入图中,直到无法继续深入为止,然后回溯到上一个节点,继续探索其他路径。这个过程会递归地进行,直到遍历完所有的节点。
2-4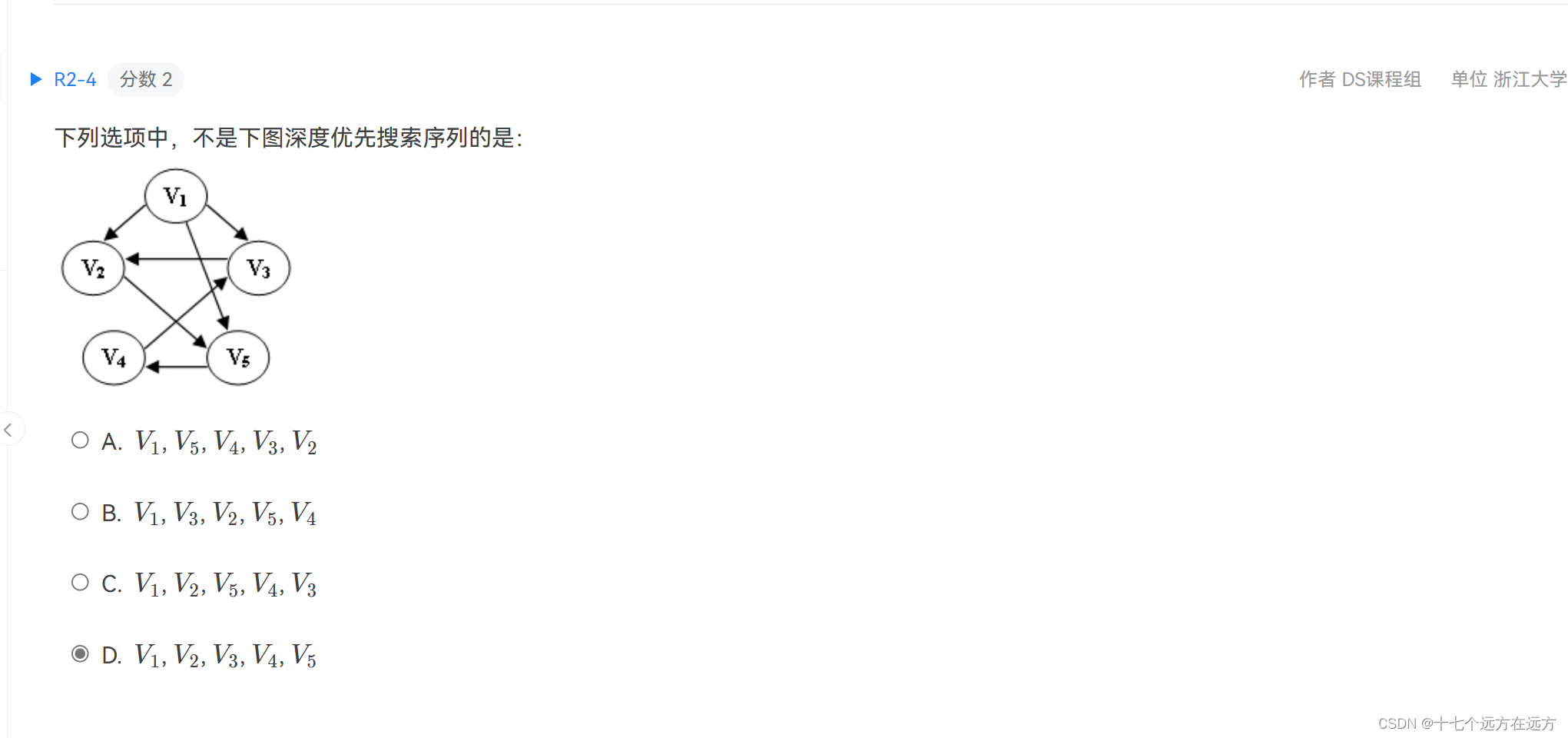
答案:D
解析:这个题没啥好说的,v2和v3之间都没有路径
2-5
答案:A
解析:没啥好说的,最短路径问题,给的答案只有迪杰斯特拉算法可以
2-6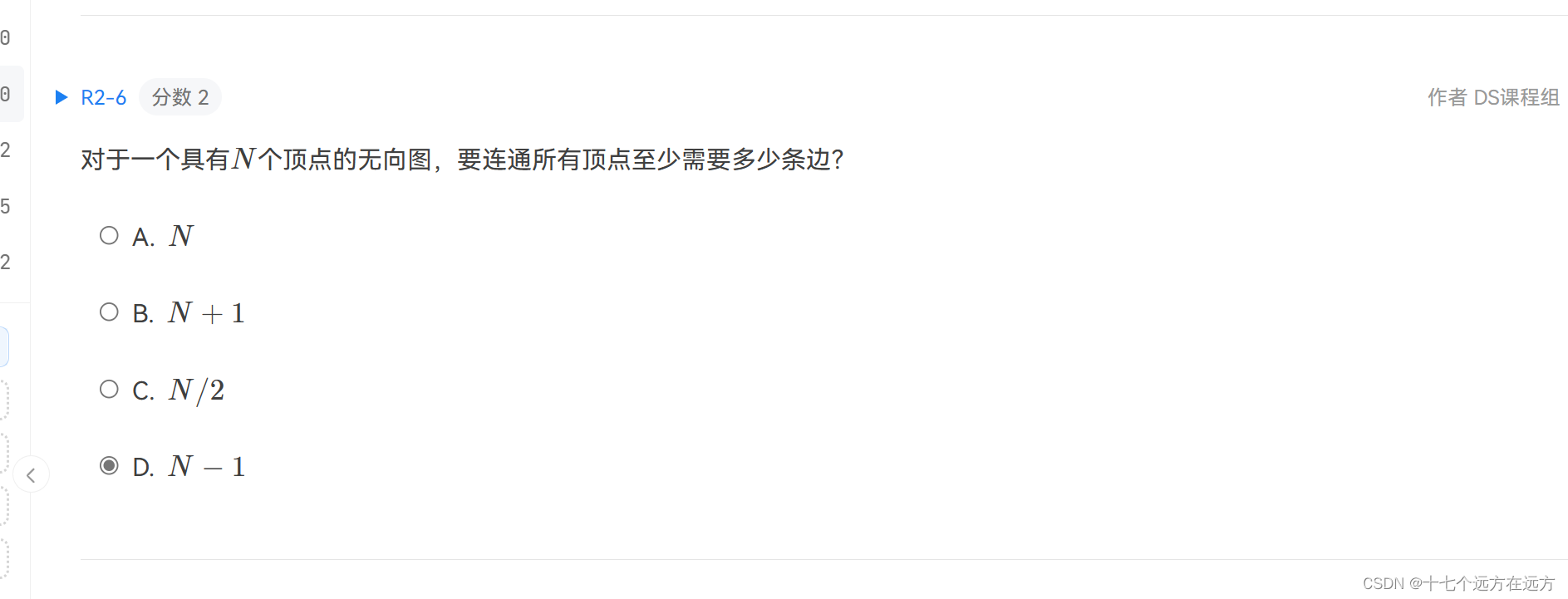
答案;D
解析:.所有顶点的度数之和 等于 边数的二倍。
2.n个顶点的无向完全图有 n(n-1)/2 条边。
3.n个顶点的连通图至少有 n-1 条边。
2-7

答案;B
解析:如果v1和v5有边,如果进行深度遍历的话就不会出现v4,v5的情况
先看A,v0和v6无所谓,因为v4,v5,v6是先访问的
再看C,v4和v6也无所谓,因为v4 v5 会先访问掉
再看D V0和V2也无所谓,因为前面这些节点都会被先访问到
2-8
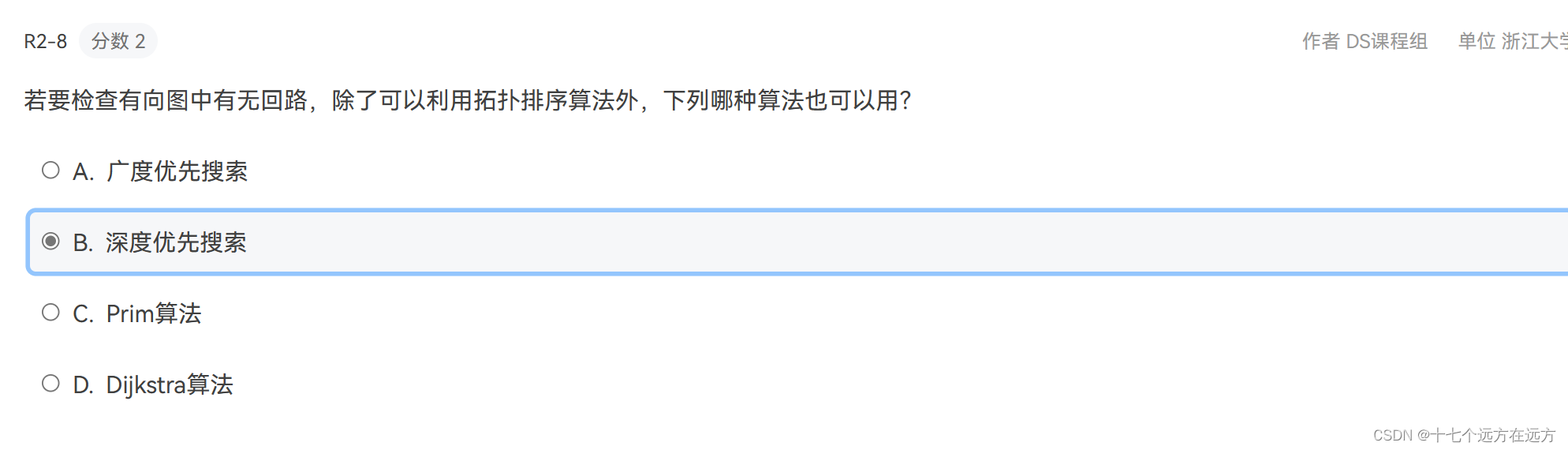
答案:B
解析:
深度优先搜索(DFS)是一种遍历图的算法,它可以用于检测有向图中是否存在回路。在深度优先搜索中,我们从一个起始节点开始,沿着一条路径尽可能深入图中,直到无法继续深入为止。如果在搜索过程中遇到已经访问过的节点,则说明存在回路。
通过使用深度优先搜索,我们可以在有向图中检测到回路的存在。如果在搜索过程中遇到一个已经访问过的节点,那么说明存在回路。
2-9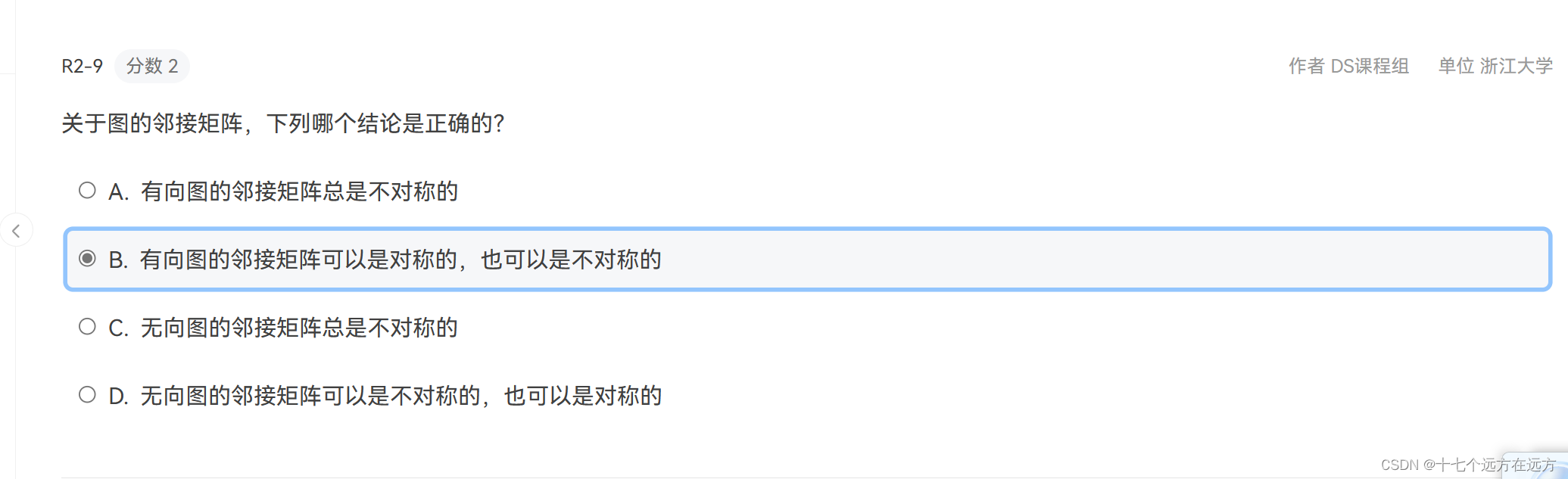
答案;B
解析:无向图肯定都是对称的,因为一个边连接两个节点,从v1可以到达v2,从v2也可以到达v1,a12=1,a21也等于1,但是对于有向图来说可以有两个顶点两条边,也可以一条边,也就是a12=1,a21不一定有边等于1
2-10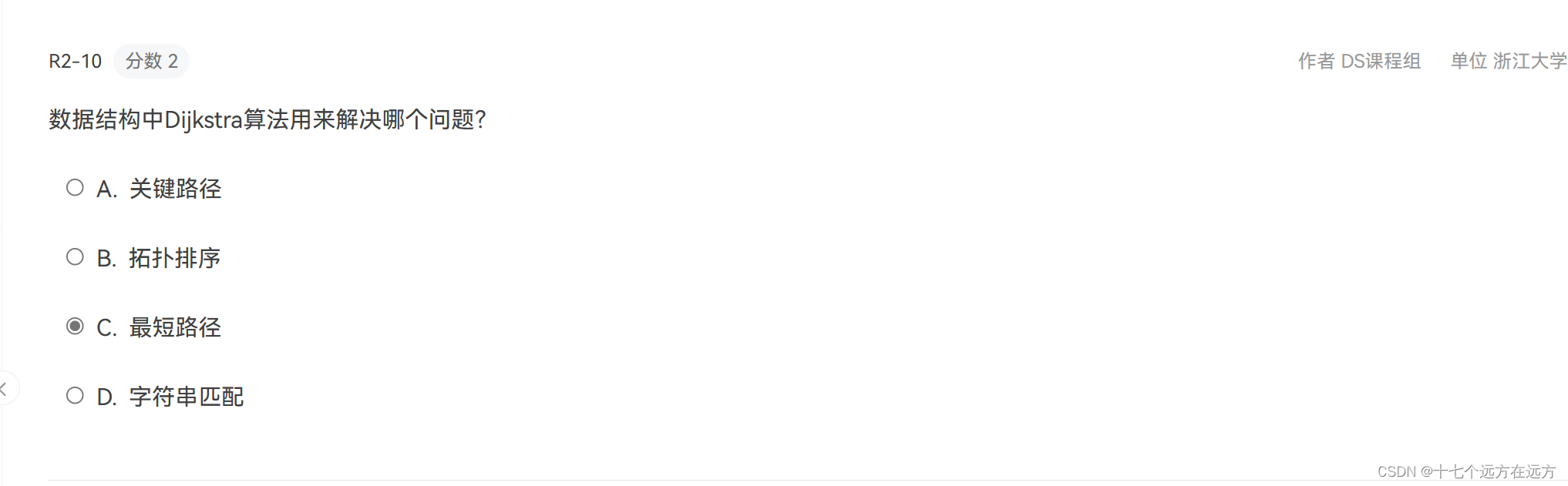
答案:C
解析:迪斯科拉算法就是为了解决最短路径问题
2-11
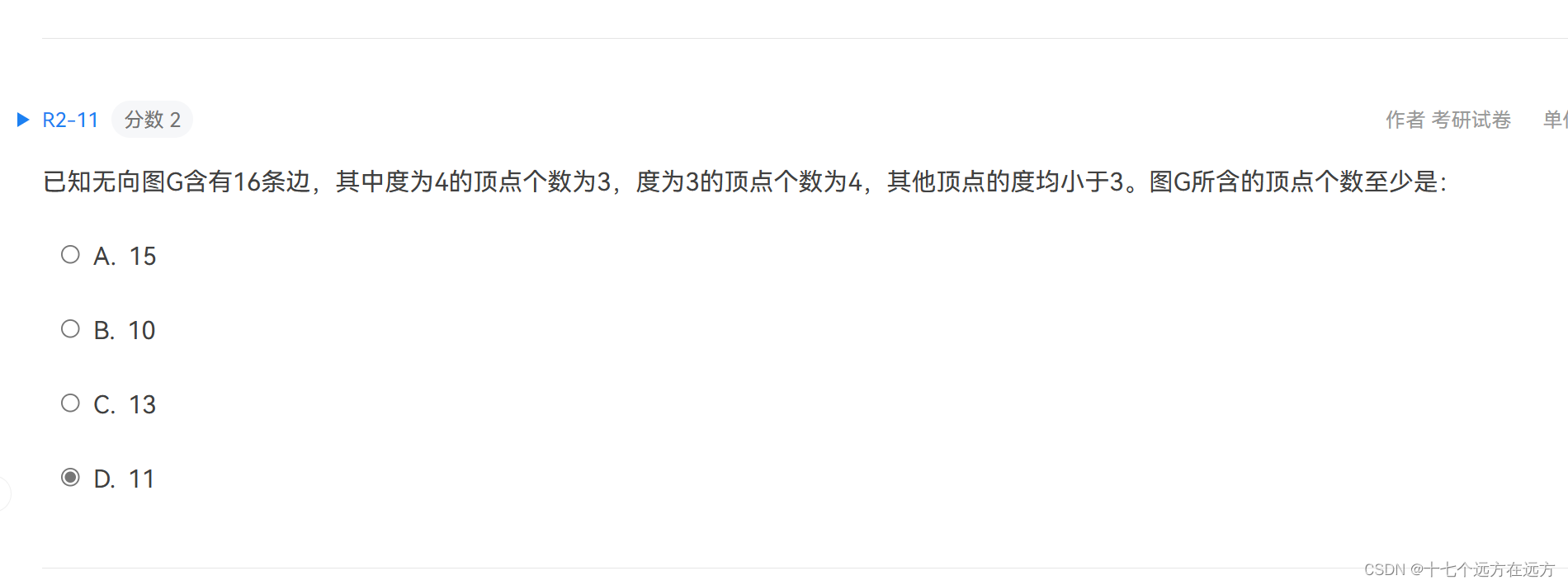
答案:D
解析:16边*2=32,32-3*12-3*12=8,其他顶点的度均小于3,可以是2,也可以是1,当为2时,8/2=4,4个顶点,此时顶点个数最少,加上之前的,3+4+4=11;
2-12
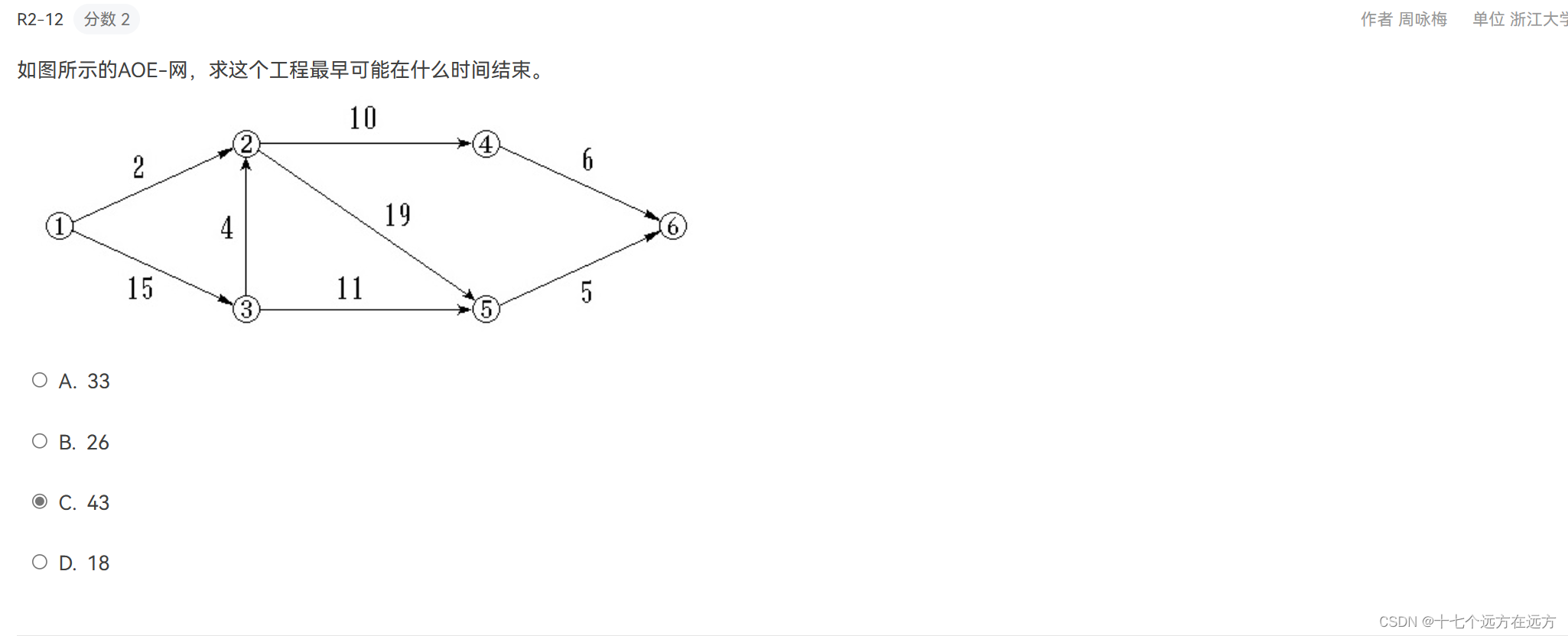
答案:C
解析:
2-13

答案:D
解析:广度优先搜索==层序遍历
从V1出发,第一层指向地址2,地址2的节点为V3,第二次指向地址1,地址1的节点为v2,第三次指向地址3,地址三的节点为v4
第二轮到V3,第一次指向地址3,地址3走过了跳过,第二次指向了地址4,地址4的节点为v5
v1->v3->v2->v4->v5;
2-14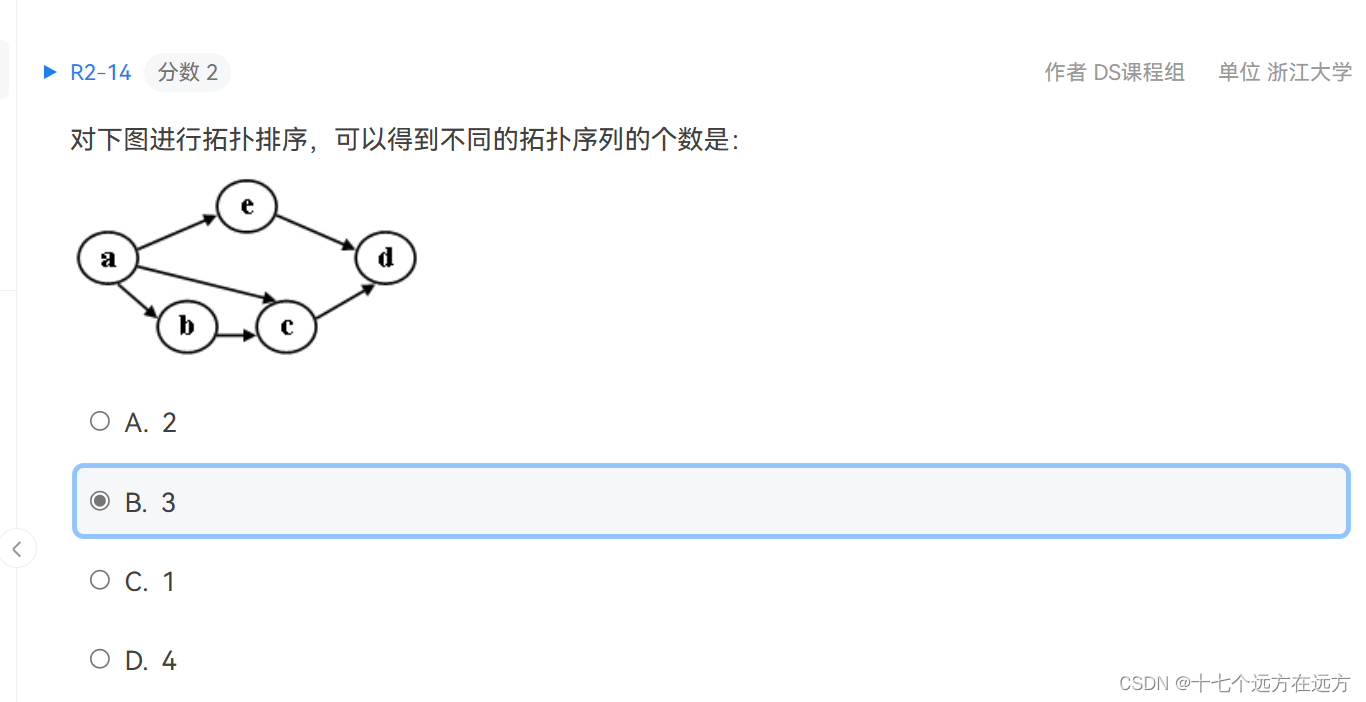
答案:B
1.a e b c d
2.a b c e d
3.a b e c d
2-15
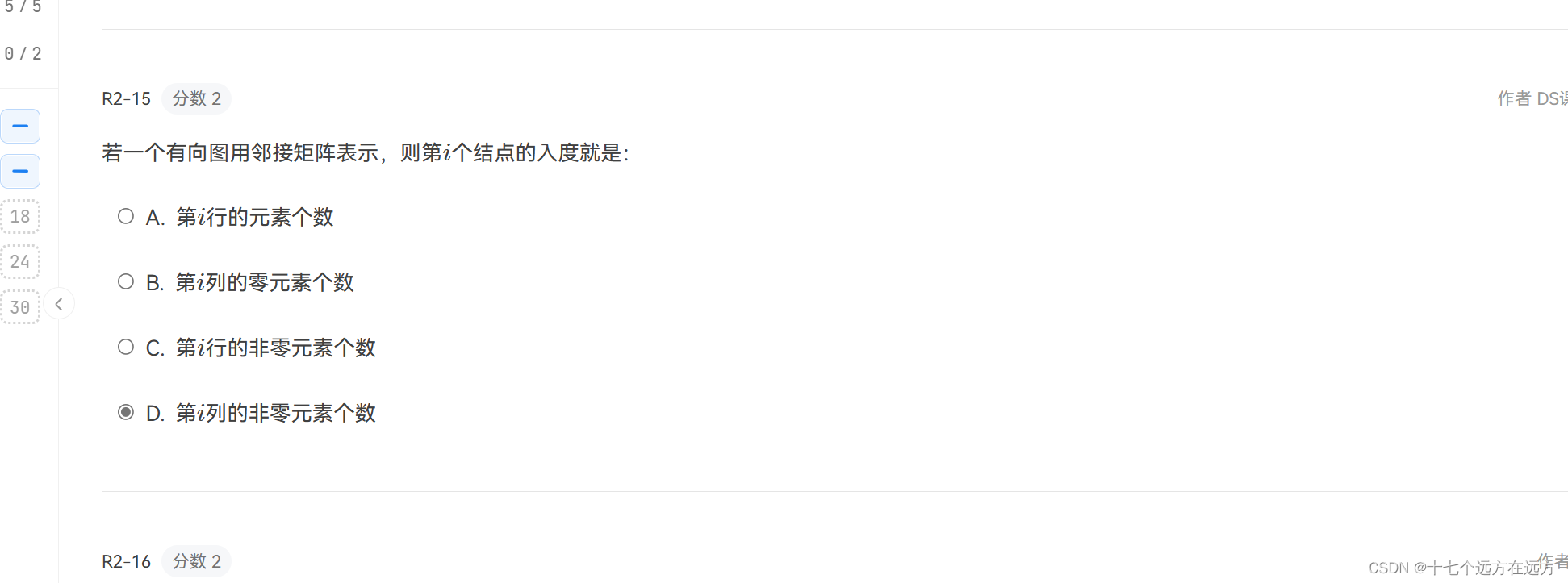
答案:D
解析:入度就是对应列标的非零元素的个数
2-16
答案:C
2-17
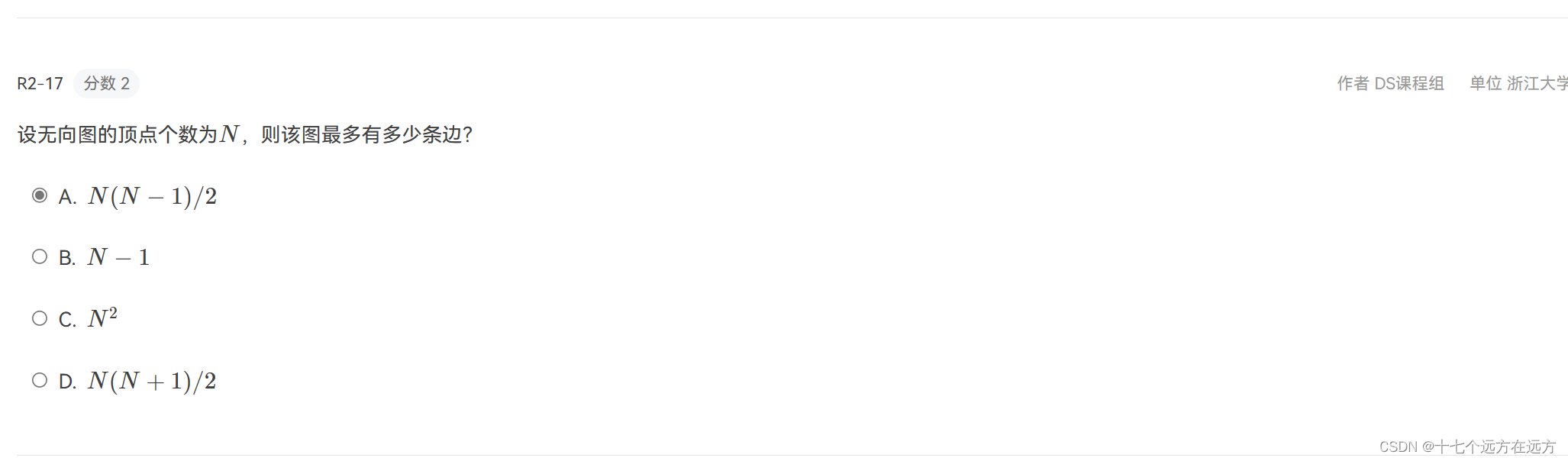
答案:A
n个顶点的完全无向图的边的n(n-1)/2;
2-18

答案:B
解析:矩阵只要顶点
邻接表是顶点数组加边实现的
2-19
答案:A
解析:不唯一,可以有多个最小生成树
2-20
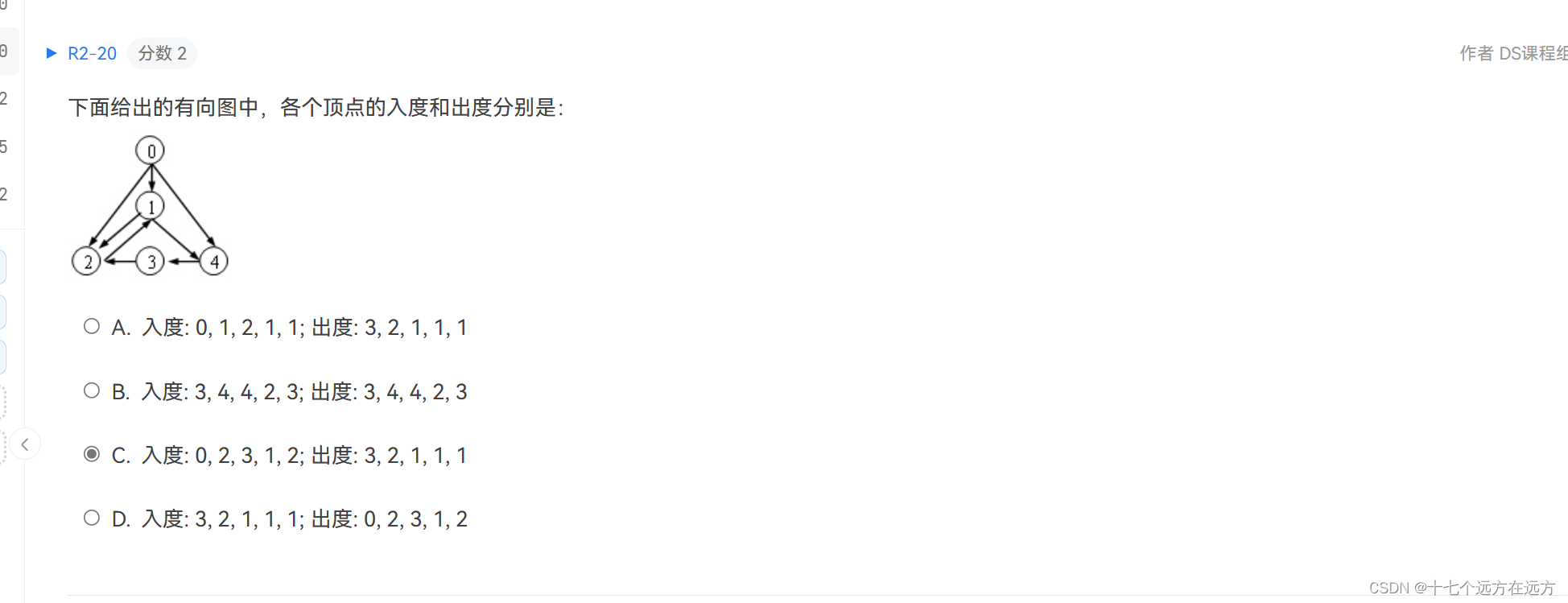
答案:C
解析:这个没啥好说的,看箭头就行了,入度是箭头指向,出度是箭头指出,查个数就行
2-21
答案:C
解析:
有向图的全部入度之和与出度之和想等,并且等于边数
1.所有顶点的度数之和 等于 边数的二倍。
2.所有顶点的入度之和 等于 出度之和。
3.n个顶点的有向完全图有n*(n-1)条边。
4.n个顶点的强连通图至少有n条边。
2-22
答案:D
解析:明显这个2不对,因为他还有前驱节点1指向他自个
2-23
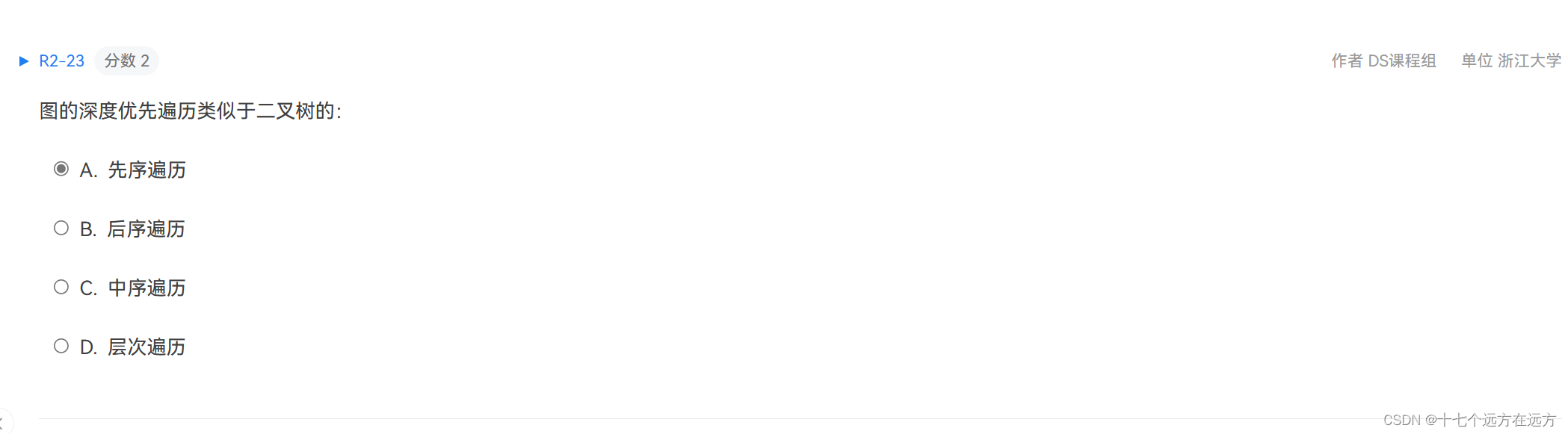
答案:A
解析:深度类似于先序遍历,没啥好说的
2-24
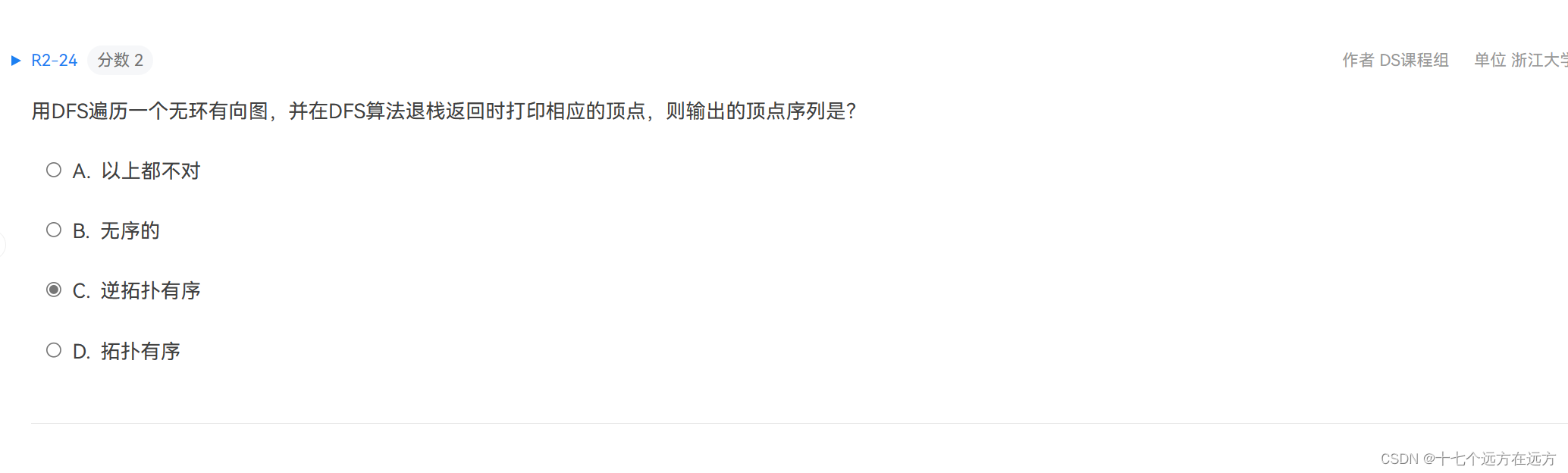
答案:C
2-25
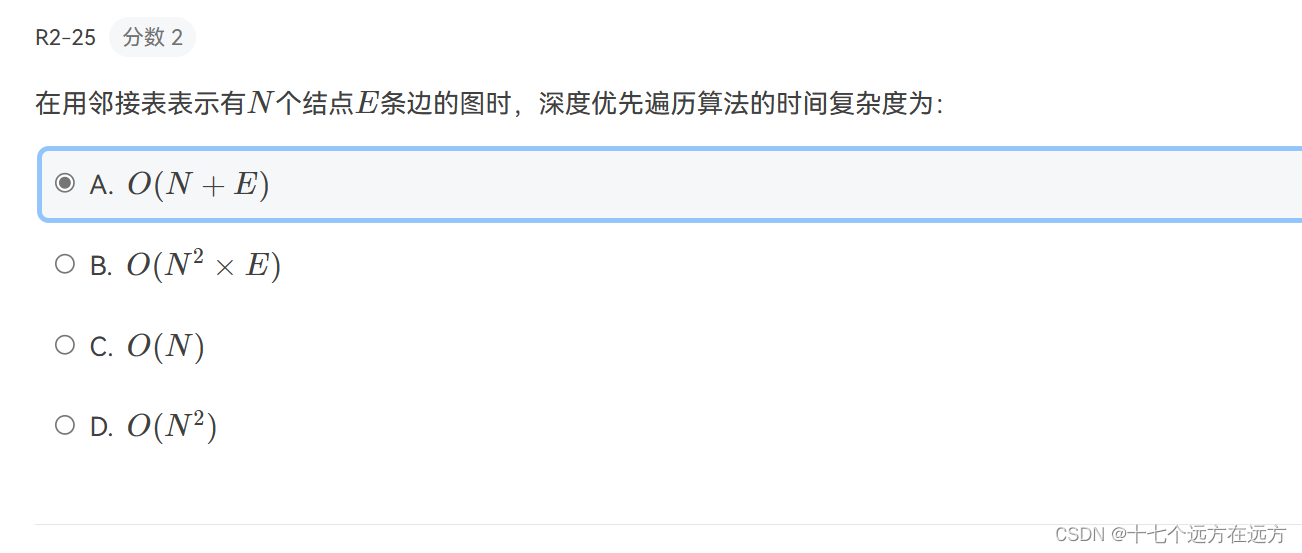
答案:A
深度优先遍历算法的时间复杂度取决于节点和边的数量。在邻接表表示中,每个节点的邻接表存储了与其相邻的节点,而每条边只会在两个节点的邻接表中出现一次。
在深度优先遍历算法中,我们会遍历每个节点,并且对于每个节点,我们会访问其邻接节点。因此,时间复杂度可以表示为O(N+E),其中N是节点的数量,E是边的数量。
2-26
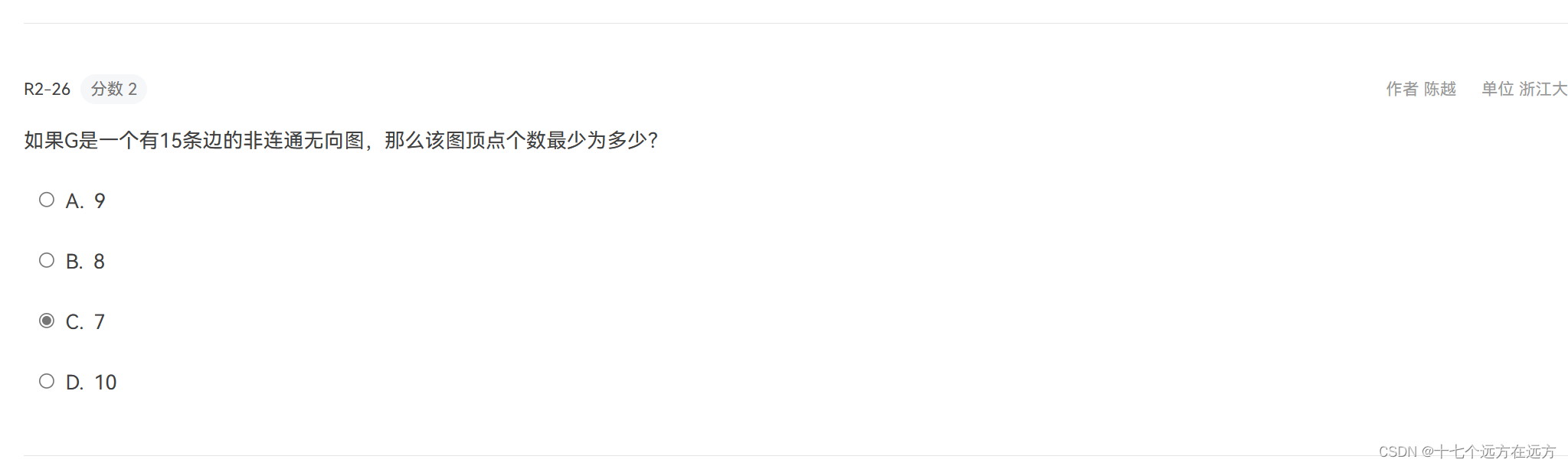
答案:7,n(n-1)/2=15;n=6,6+1=7;
2-27
答案:B
解析:邻接表查入度需要遍历所有节点。
2-28
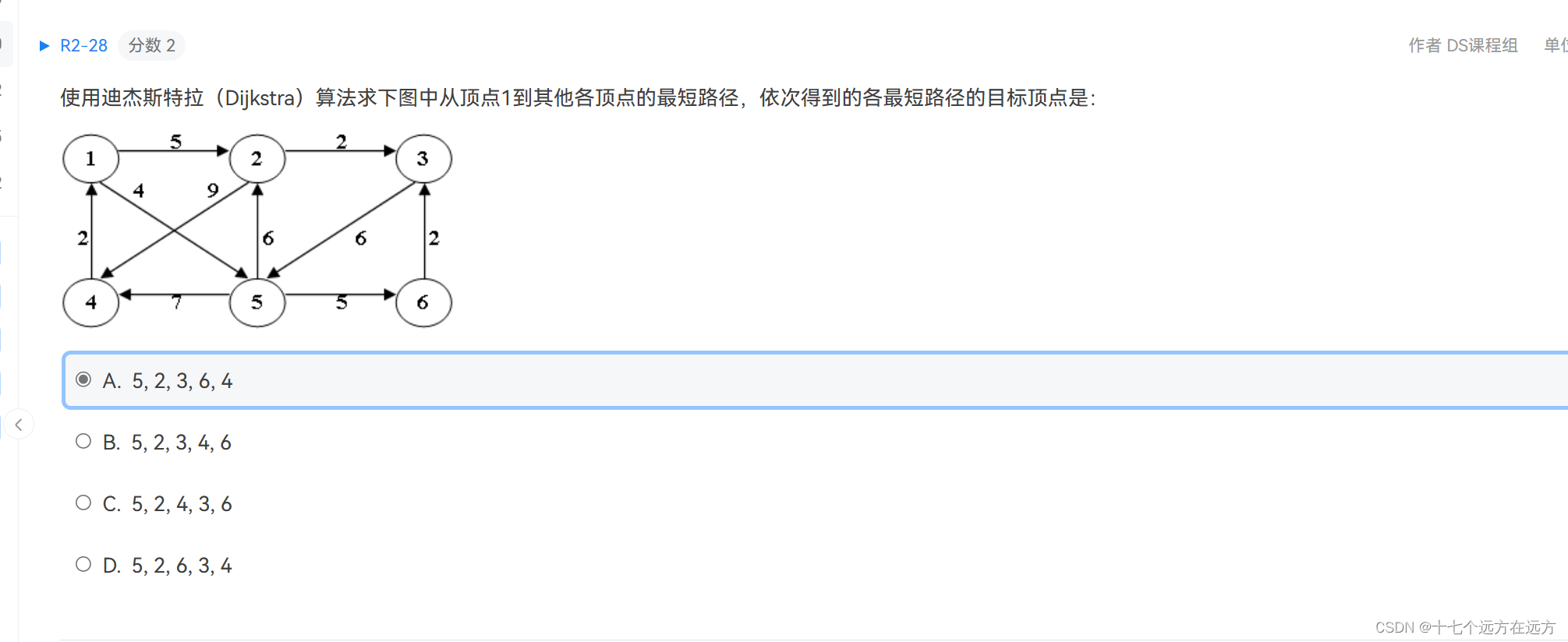
答案:A
解析:4的路径长度为14最大,3的最短路径长度为7,6的最短路径长度为9
2-29
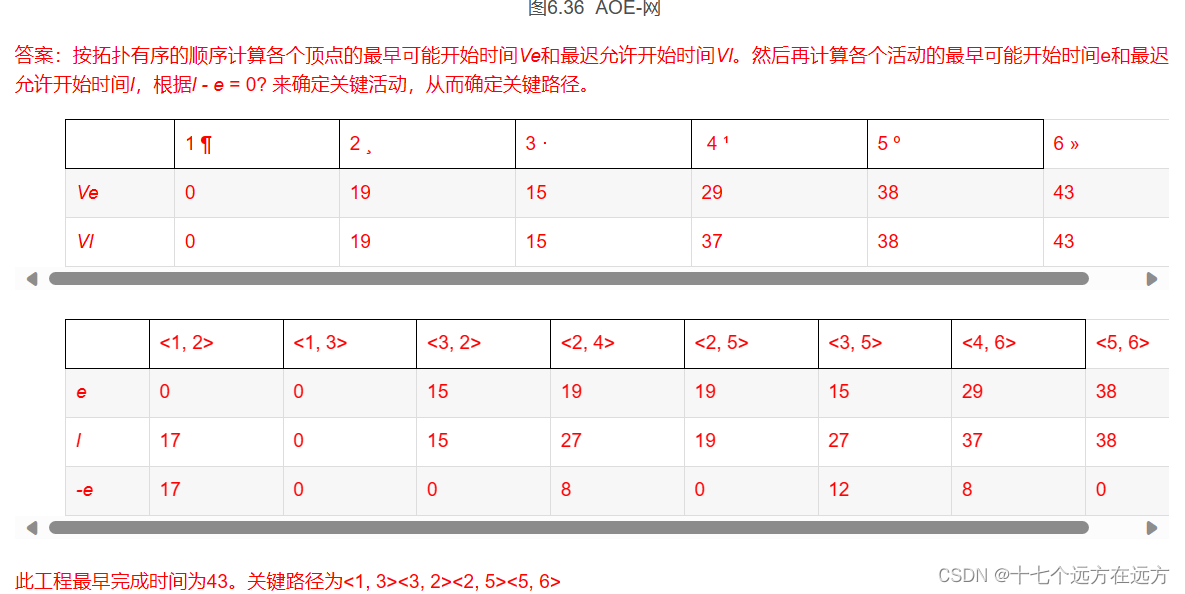
答案:D
在AOE网中,从源点到汇点最长的路径称为关键路径
2-30

答案:C
肯定是连通的,如果不连通,从某一顶点出发无法访问到其他全部顶点




![[蓝桥杯 2019 省 B] 特别数的和-C语言的解法](https://img-blog.csdnimg.cn/65eed59a4f1044378c95f3d03e7d3cd1.png)

![[论文阅读]Generalized Attention——空间注意力机制](https://img-blog.csdnimg.cn/direct/07f66202a6d842c5b395748444d84719.png)