多项式拟合求解

news2025/2/25 11:20:45

简介

基本原理

例1

例2

例3

参考资料

简介

多项式拟合可以用最小二乘求解，不管是一元高阶函数，还是多元多项式函数，还是二者的混合，都可以通过统一的方法求解。当然除了最小二乘法，还是其他方法可以求解，比如迭代的梯度下降法，这里重点介绍最小二乘法求解。

基本原理

多项式拟合，目标函数可以表示为

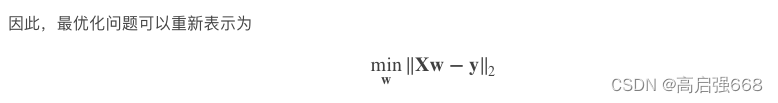
对目标函数求导，再令导数为0，即可求解。

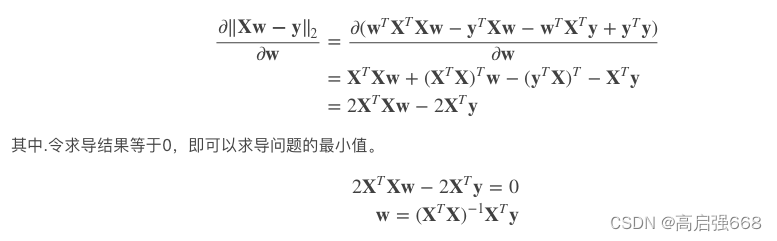
例1

比如函数形式为：

y = a0 + a1*x + a2*x*x + a3*x*x*x

这里以3阶为例，通过N组数据（N>=4）拟合出系数a0,a1,a2,a3，则可以用最小二乘法求解

A = inv(M.T @ M) @ M @ Y

M矩阵是N x 4, 其中的4为[1, x, x*x, x*x*x]

Y是列N x 1，求得的A为4 x 1

如果是N阶的，只要把4替换成N+1即可。

例2

比如函数形式为

y = a0 + a1 * x1 * x2 这种形式，是两元函数，也可以用类似的方法求解。其中的M矩阵是N x 2的，其中的2为[1, x1*x2]。这些拟合其实也可以通过Python函数库curve_fit来求解，具体可以参考如下代码。代码里使用curve_fit求解了，使用最小二乘也求解了，得到的结果非常接近。

import os
import cv2
import random
import copy
import numpy as np
import math
from scipy.optimize import curve_fit


def func1(x, a, b):
    r = a + b * x[0] * x[1]
    return r.ravel()

def LeastSquare(M, Y):
    # y = M @ x, 求解X，y:nx1  M:n * xs  x: xs * 1
    X = np.linalg.inv(M.T @ M) @ M.T @ Y
    return X


def Test():
    # xx = np.indices([4, 2])
    xx = np.random.random([2, 4])
    y = 10 + 5 * xx[0, :] * xx[1, :]
    print(xx)
    print(y)
    z = func1(xx, 10, 5) + np.random.normal(size=4)/100
    # z = func1(xx, 10, 5)
    print(z)
    prot, tmp = curve_fit(func1, xx, z)
    print('curve_fit:', prot)
    print('误差：', tmp)

    matM = np.ones((4, 2), np.float32)
    for i in range(4):
        matM[i, 1] = xx[0, i] * xx[1, i]
    out = LeastSquare(matM, z.reshape(-1, 1))
    print('least square:', out)


if __name__ == "__main__":
    Test()

运行的结果如下，可以看到二者的结果非常接近。

[[0.16495595 0.75923904 0.83520597 0.64013137]
 [0.04531869 0.68136656 0.54886631 0.18077084]]
[10.03737794 12.58660045 12.29208211 10.57858545]
[10.0294282  12.5906653  12.29289287 10.57768172]
curve_fit: [9.99406627 5.01797846]
误差： [[ 5.20691649e-06 -1.16488038e-05]
 [-1.16488038e-05  4.24005611e-05]]
least square: [[9.99406455]
 [5.01798235]]

例3

比如函数形式为

y = a0 + a1 * x1 * x2 + a2 * x2 * x3 + a3 * x1 * x3 + a4 * x1 * x2 * x3

求解中，M矩阵为N x 5，其中的5为[1, x1*x2, x2*x3, x1*x3, x1*x2*x3]，类似例2中，使用相似的方法，构造出M矩阵，Y的数据，就可以求解出a0, a1, a2, a3, a4。

这里以这三个例子来说明，主要是最近做数据拟合时，会使用到这三种形式，之前都是通过调用curve_fit函数来实现，如果写成C代码，就可以使用最小二乘，不过中间有求逆运算，可能还是要调用第三方库函数来实现，这三种例子里涉及的求逆运算主要有4阶，2阶和5阶，如果形式固定，自己编写C代码实现求逆运算也是可以的。