1 基本概念
-
智能体 agent ,做动作的主体,(大模型中的AI agent)
-
环境 environment:与智能体交互的对象
-
状态 state ;当前所处状态,如围棋棋局
-
动作 action:执行的动作,如围棋可落子点
-
奖励 reward:执行当前动作得到的奖励,(大模型中的奖励模型)
-
策略 policy: π ( a ∣ s ) \pi(a|s) π(a∣s) 当前状态如何选择action,如当前棋局,落子每个点的策略
-
回报(累计奖励) return : 是从当前时刻开始到本回合结束的所有奖励的总和, U t = R t + γ R t + 1 + γ 2 R t + 2 + γ 3 R t + 3 . . . . U_t=R_t+\gamma R_{t+1}+\gamma^2R{t+2}+\gamma^3R{t+3} .... Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3....
-
折扣回报 𝛾:
-
动作价值函数: Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi (s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t] Qπ(st,at)=E[Ut∣St=st,At=at]
-
最优动作价值函数: Q ∗ ( s t , a t ) = m a x π Q π ( s t , a t ) Q^*(s_t,a_t)=max_\pi Q_\pi(s_t,a_t) Q∗(st,at)=maxπQπ(st,at)
-
状态价值函数: V π ( s t ) = E A [ Q π ( s t , A ) ] V_\pi (s_t)=E_A[Q_\pi(s_t,A)] Vπ(st)=EA[Qπ(st,A)]
2 DQN
折扣回报:
U
t
=
R
t
+
γ
R
t
+
1
+
γ
2
R
t
+
2
+
γ
3
R
t
+
3
.
.
.
.
U_t=R_t+\gamma R_{t+1}+\gamma^2R{t+2}+\gamma^3R{t+3} ....
Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3....
动作价值函数:
Q
π
(
s
t
,
a
t
)
=
E
[
U
t
∣
S
t
=
s
t
,
A
t
=
a
t
]
Q_\pi (s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t]
Qπ(st,at)=E[Ut∣St=st,At=at]
最优动作价值函数:
Q
∗
(
s
t
,
a
t
)
=
m
a
x
π
Q
π
(
s
t
,
a
t
)
Q^*(s_t,a_t)=max_\pi Q_\pi(s_t,a_t)
Q∗(st,at)=maxπQπ(st,at)
核心公式:时间差分算法
Q
(
s
t
,
a
t
;
w
)
=
r
t
+
γ
max
a
∈
A
Q
(
s
t
+
1
,
a
;
w
)
Q(s_t,a_t;w)=r_t+\gamma \max _{a\in A}Q(s_{t+1},a;w)
Q(st,at;w)=rt+γmaxa∈AQ(st+1,a;w)
证明:略
公式解读及注意事项:
输入:(
s
t
,
a
t
,
r
t
,
s
t
+
1
s_t,a_t,r_t,s_{t+1}
st,at,rt,st+1)
左边项
Q
(
s
t
,
a
t
;
w
)
Q(s_t,a_t;w)
Q(st,at;w) : 是神经网络在t时刻的预测
右边
r
t
r_t
rt是当前奖励值,
max
a
∈
A
Q
(
s
t
+
1
,
a
;
w
)
\max _{a\in A}Q(s_{t+1},a;w)
maxa∈AQ(st+1,a;w)
目标:使左右两边误差最小。
DQN 是对最优动作价值函数 Q⋆ 的近似。DQN 的输入是当前状态 st,输出是每个动作的 Q 值。DQN 要求动作空间 A 是离散集合
DQN高估问题:
1 最大化导致高估, 上式中总是取最大值,会导致高估
2 自举导致高估 上式中目标函数也用自己,使用自己估计自己,会导致高估
因此可以对目标函数进行以下改进。
目标函数分析:
Q ( s t , a t ; w ) = r t + γ max a ∈ A Q ( s t + 1 , a ; w ) Q(s_t,a_t;w)=r_t+\gamma \max _{a\in A}Q(s_{t+1},a;w) Q(st,at;w)=rt+γmaxa∈AQ(st+1,a;w)
- a .左右两边可以使用统一个Q函数
b. 左右两边使用不同Q函数
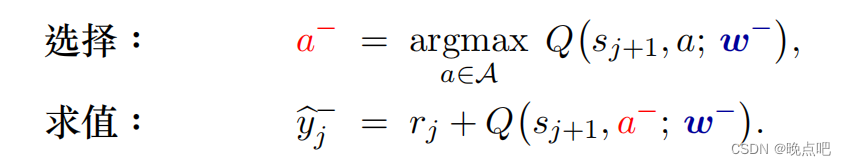
c. 左右两边使用不同Q函数,且target 的
Q
t
a
r
g
e
t
(
s
t
+
1
,
a
;
w
)
Q_{target}(s_{t+1},a;w)
Qtarget(st+1,a;w) 的a 来自第一个函数
max
a
∈
A
Q
1
(
s
t
+
1
,
a
;
w
)
\max _{a\in A}Q_1(s_{t+1},a;w)
maxa∈AQ1(st+1,a;w)

- 高估解决办法:
b 策略可以减少自举带来的高估
c 策略一定程度上能减少最大化带来的高估,因为用第一个Q函数中的a,在 Q t a r g e t Q_{target} Qtarget中总是小于等于最大值的 max a ∈ A Q t a r g e t ( s t + 1 , a ; w ) \max _{a\in A}Q_{target}(s_{t+1},a;w) maxa∈AQtarget(st+1,a;w) (DDQN方法)
3 核心代码实现DQN,DDQN
DQN 如下代码,
self.model为Q函数
self.model_target为目标Q函数,
s_batch :当前状态
a_batch:当前执行动作
r_batch: 奖励
d_batch ; 是否游戏结束
next_s_batch; 执行动作a_batch后,到下一个状态
self.model在当前状态s_batch下得到每个状态的Q值,选择a_batch对应的Q值,即为当前Q值
self.target_model 在下一步状态next_s_batch下,取self.target_model 最大值对应到a的值(DDQN,是在self.target_model中取self.model最大值对应a的值)。
def compute_loss(self, s_batch, a_batch, r_batch, d_batch, next_s_batch):
# Compute current Q value based on current states and actions.
qvals = self.model(s_batch).gather(1, a_batch.unsqueeze(1)).squeeze()
# next state的value不参与导数计算,避免不收敛。
next_qvals, _ = self.target_model(next_s_batch).detach().max(dim=1)
loss = F.mse_loss(r_batch + self.discount * next_qvals * (1 - d_batch), qvals)
return loss
DDQN
与上面唯一区别是:使用Q1函数中的a
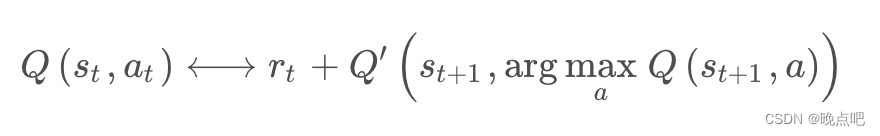
def compute_loss(self, s_batch, a_batch, r_batch, d_batch, next_s_batch):
# Compute current Q value based on current states and actions.
Q1=self.model(s_batch)
qvals =Q1 .gather(1, a_batch.unsqueeze(1)).squeeze()
a_target =Q1argmax()
# next state的value不参与导数计算,避免不收敛。
next_qvals = self.target_model(next_s_batch).detach().gather(1, a_target).squeeze()
loss = F.mse_loss(r_batch + self.discount * next_qvals * (1 - d_batch), qvals)
return loss
def get_action(self, obs):
qvals = self.model(obs)
return