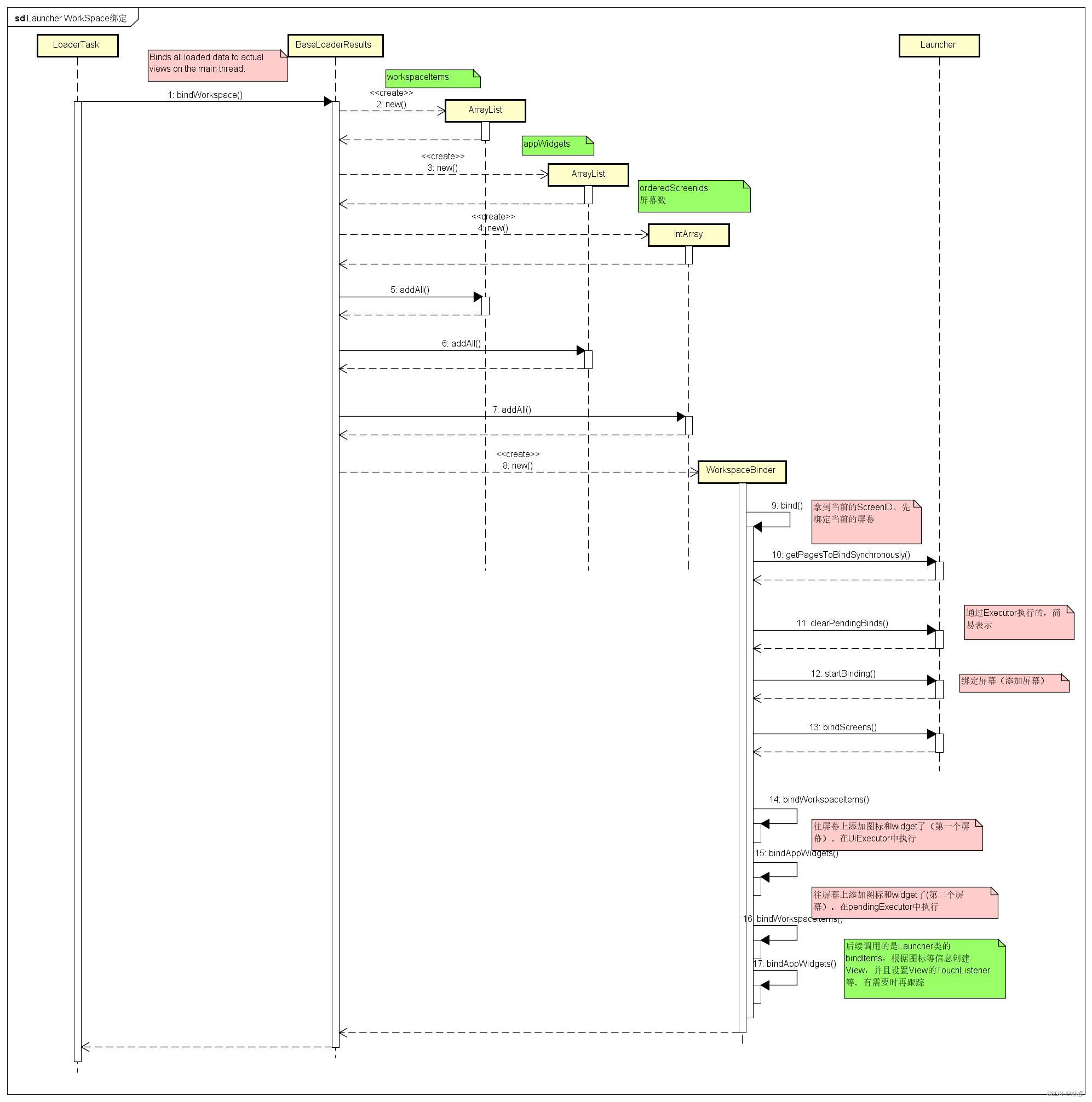
先前发了几篇五子棋游戏程序设计的博文,设计了游戏程序,也设计了AI智能奕棋的算法,运行程序检测算法的可行性,完成人机模式游戏功能的设置。
本文主要介绍自动测试算法的方法。
AI智能奕棋的算法testAIq( ),主要是检测算法,测试算法的可行性。程序设置的对战演示就是为了测试算法,此为研究五子棋算法提供一些参考。
在检测算法的可行性时感到很烦,老是要一步步试走黑棋和白棋。就设计了自动测试的方法。
autoplay ( ) { //自动演示,检测算法
//*用于检测AI智能下子算法 testAIq ()
s7="游戏模式:自动演示 ";
if (mode==1) return ; //双人模式可演示
if (isDo==0) return ; //isDo 游戏可行控制
if (dn==0) { //设定首子黑先天元位, dn下子序,0为首子
n=113; wn=0 ; black_do () ; } //棋盘位数组 0-225
for (ti=1; ti<=6; ti++) { //每次3个回合
if(isDo==0) return ; //若取胜则跳出
wn=wn+1 ;
testAIq (); //AI 算法测试 *return sn
if (wn>1) wn=0 ; //轮流下子
n=sn ; //n为绘出棋子位号
if (wn==0) pn[n]=1 ; //黑棋下子
if (wn==1) pn[n]=2; //白棋下子
row=15-(n/15) ; //n转换成行列,显示下子位H8 G9 ...
col=(n-(n/15*15)) ;
if (col==0) { col=15 ; row=row+1 ; }
swapabc () ; //return ss
if(ss=="I") ss=ss+" " ;
//print 走子记录
if (wn==0) cordp=" B "+intToString (n);
if (wn==1) cordp=" W "+intToString (n);
if (cordp != ss2) {
dn=dn+1;
print dn," ",cordp," " , ss,row ; //打印记录
ss2=cordp;
dwn[dn]=n ; //print play number
fudat[dn]=n; fusum=dn; //复盘数据
board () ; //重绘棋盘,显示棋子
}
detect (); //检测胜负
} //next ti
}//autoplay ( )

对于人机对战的电脑智能应子算法,参阅很多五子棋书籍棋谱和五子棋竞赛的对抗棋谱。我感到白棋的后手防御算法很难取胜,棋界有黑棋高手先手必胜一说。算法么想了很多,既然是人工智能下棋就得按人的思路来算计。棋书阐述有许多思路和棋局解说。如活四冲四,嵌五,活三嵌四,活二嵌二。这些是高级棋手的总结。我就按此思路用加权计权方法来表现此类各种情况。
我对算法的思路是:黑棋的进攻点就是白棋的防守点,反之,白棋的进攻点就是黑棋的防守点。我采用一次遍历棋盘各点位的方法,凡有黑子和白子就判断其四周的空白点,即可下子位,评估棋势加权计分。棋势就是单子、活二嵌二、活三嵌三嵌四、活四冲四嵌五。各个棋势的交点就叠加计分,高分点就是双方博弈的必争点。算法的要点是:独子成二是起点,连二到连三是重点,关键的要点是三连子到四连五连。这这三点就分出权重的棋势。活三02220两边的点位是,先手是绝杀点,后手是防守逢三必堵。眠三122200棋势,空位下子成冲四,这是抢先手来改势扩势来进攻。若抓到冲四加活三叠加进攻点,权分叠加计权,就能绝杀对方。我的算法思路就这样。算法想白棋后手取胜,就在白棋的棋势上加小分,这样利于白棋在同等情况下能争得先手,反战进攻取胜。想法很简单,写算法也不难,而对于棋势的加权分的估量较难。
五子棋游戏程序的源码可参阅我本站的几篇博文。