TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
举个例子:
有十亿个整形数据,我们的内存时4G,也就是102410241024*8个字节的空间,十亿个整形数据需要的是40亿个字节的空间,就占了内存的一半空间,这是不可行的
最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素,将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素
下面我们进行代码的实现:
首先我们生成1000个随机数,范围再十万以内,放入一个数组中:
srand(time(0));
int* a = (int*)malloc(sizeof(int) * 1000);
if (a == NULL)
{
perror("malloc");
return 0;
}
for (size_t i = 0; i < 1000; i++)
{
a[i] = rand() % 100000;
}
然后我们随机将数组中的任意k个元素改为超过十万的数字,方便验证:
a[7] = 100000 + 1;
a[49] = 100000 + 2;
a[123] = 100000 + 3;
a[456] = 100000 + 4;
a[789] = 100000 + 5;
我们还要用到向下调整算法,以便于建堆:
void swap(int* p1, int* p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = (parent * 2) + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
{
child++;
}
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
parent=child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
最后我们将a数组中的前k个元素插入到top_k函数的数组里,然后进行一次向下调整算法,将其调整为大堆,然后再用剩下的n-k个元素与堆顶元素进行比较,如果比他大进替换进堆,然后进行向下调整
void top_k(int* a, int n, int k)
{
int i = 0;
int* top = (int*)malloc(sizeof(int) * k);
if (top == NULL)
{
perror("malloc");
return;
}
for (i = 0; i < k; i++)
{
top[i] = a[i];
}
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(top, k, i);
}
for (i = k; i < 1000; i++)
{
if (a[i] > top[0])
{
top[0] = a[i];
AdjustDown(top, k, 0);
}
}
完整代码如下:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<assert.h>
void swap(int* p1, int* p2)
{
int temp = *p1;
*p1 = *p2;
*p2 = temp;
}
void AdjustDown(int* a, int n, int parent)
{
int child = (parent * 2) + 1;
while (child < n)
{
if (child + 1 < n && a[child + 1] < a[child])
{
child++;
}
if (a[child] < a[parent])
{
swap(&a[child], &a[parent]);
parent=child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void top_k(int* a, int n, int k)
{
int i = 0;
int* top = (int*)malloc(sizeof(int) * k);
if (top == NULL)
{
perror("malloc");
return;
}
for (i = 0; i < k; i++)
{
top[i] = a[i];
}
for (i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(top, k, i);
}
for (i = k; i < 1000; i++)
{
if (a[i] > top[0])
{
top[0] = a[i];
AdjustDown(top, k, 0);
}
}
for (i = 0; i < k; i++)
{
printf("%d ", top[i]);
}
free(top);
}
int main()
{
srand(time(0));
int* a = (int*)malloc(sizeof(int) * 1000);
if (a == NULL)
{
perror("malloc");
return 0;
}
for (size_t i = 0; i < 1000; i++)
{
a[i] = rand() % 100000;
}
a[7] = 100000 + 1;
a[49] = 100000 + 2;
a[123] = 100000 + 3;
a[456] = 100000 + 4;
a[789] = 100000 + 5;
int k = 5;
top_k(a, 1000, k);
}
向上调整算法和向下调整算法的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值,多几个节点不影响最终结果):

我们令高度为h,节点个数n就等于2^(h)-1个
那么在向上调整算法中:
最坏情况下,最后一层的节点需要向上移动h-1次,依次类推,就得到总次数的表达式,然后再用错位相减法和n和h的关系就能求出时间复杂度f(n)了
在向下调整算法中:
最坏情况下,倒数第二层节点向下只移动一次,第一层最多移动h-1次
总结下来我们就会发现,向上调整算法中是多节点乘多层数的关系,而向下调整算法则是多节点乘少层数的关系,我们进行比较就会发现其实向下调整算法的效率更高,所以在平常的排序和建堆中我们 最常用的还是向下调整算法
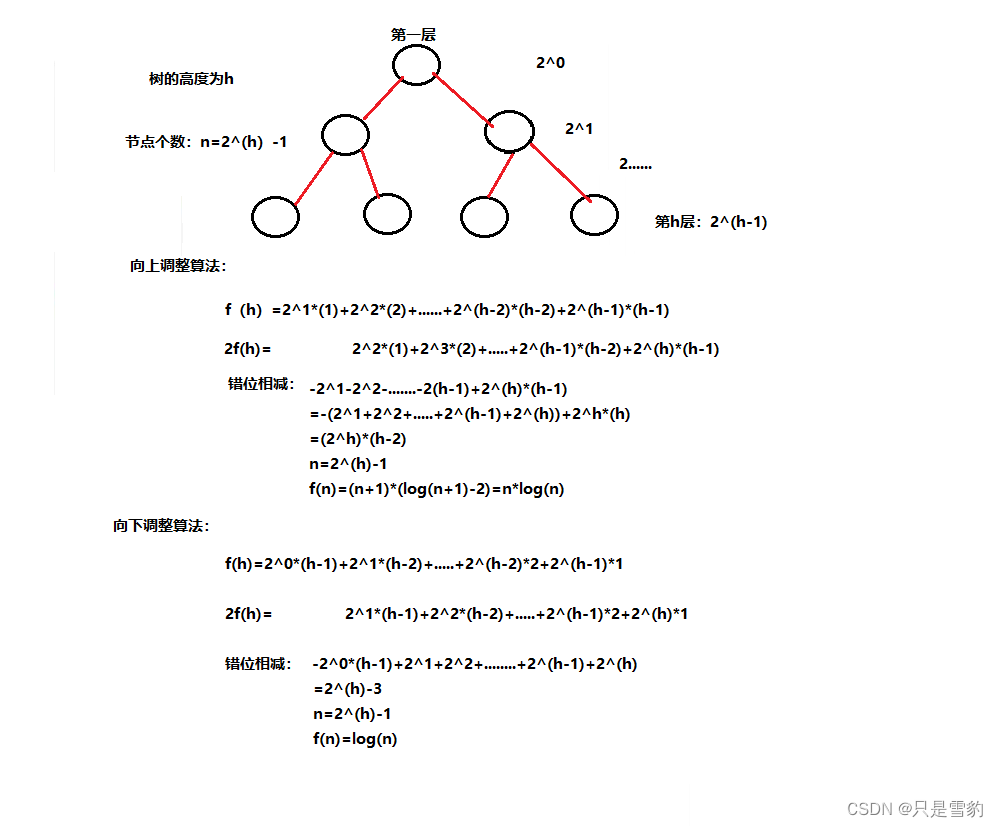
向上调整算法的时间复杂度为:
n*log(n)
向下调整算法的时间复杂度为:
log(n)
因此,向下调整算法的效率是远大于向上调整算法的!
好了,今天的分享到这里就结束了,谢谢大家的支持!