【算法】动态规划中的路径问题

在这里插入图片描述

君兮_的个人主页

即使走的再远，也勿忘启程时的初心

C/C++ 游戏开发

Hello,米娜桑们，这里是君兮_，如果给算法的难度和复杂度排一个排名，那么动态规划算法一定名列前茅。今天，我们通过由简单到困难的两道题目带大家学会动态规划中的路径问题

好了废话不多说，开始我们今天的学习吧！！

动态规划之路径问题

一不同路径
- 1 题目解析
- 2 算法原理
- - 状态表示
  - 状态转移方程
  - 初始化
  - - 辅助节点初始化法
  - 填表顺序：
  - 返回值
- 3 编写代码
二下降路径最小和
- 1 题目解析
- 2 算法原理
- - 状态表示
  - 状态转移方程
  - 初始化
  - 填表顺序
  - 返回值
- 3 编写代码
总结

一不同路径

原题目leetcode链接在这哦不同路径

1 题目解析

如题目所示，在左上角有一个机器人，现在我们需要算出从当前位置到右下角位置一个有多少种不同的路径。
注意：重点在于，我们是不能后退的，也就是说，每次进行移动时，只能朝右或者朝下移动。

题目题意理解相对比较简单，就先说到这里

2 算法原理

看到这种每一步都与上面一步有所关系的题目，我们首先想到的就是动态规划算法，我们来按照之前提到的动态算法的大致解题思路来进行一步步的分析

状态表示

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：
i. 从dp[i, j] 位置出发，到某个位置去；
ii. 从起始位置出发，到达dp [i, j] 位置。
分析一下题意，我们需要到达指定的位置，因此这⾥选择第⼆种定义状态表⽰的⽅式：
dp[i][j] 表⽰：⾛到dp[i, j] 位置处，此时一共有几条不同路径

状态转移方程

有了上面的状态表示，我们就需要将dp每个位置的值建立一定的联系，方便我们之后的分析
如果dp[i][j] 表⽰到达 [i, j] 位置的⽅法数，那么到达 [i, j] 位置之前的⼀⼩步，有两种情况：
i. 从dp [i, j] 位置的上⽅（ dp[i - 1, j] 的位置）向下⾛⼀步，转移到 dp[i, j] 位置；
ii. 从 dp[i, j] 位置的左⽅（ dp[i, j - 1] 的位置）向右⾛⼀步，转移到 dp[i, j] 位置。
由于我们要求的是有多少种⽅法，结合我们上面对题目的解析，因此我们的状态转移⽅程就可以写出了：

 dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

注意：这里还有一个很多初学者容易搞混的地方——很多人认为，你现在算出的是通往dp[i][j]这里不同种方法，那么dp[i][j]这一步不应该再加个1吗？
谨记我们这里算的是方法数，不是步数，因此当然不需要+1！

初始化

初始化的主要目的有两个，
1.防止发生越界访问
2.方便我们从已知的信息推出我们需要的信息

这里教给大家一个做动态规划会经常使用的初始化方法

辅助节点初始化法

可以在dp表最前⾯加上⼀个「辅助结点」，帮助我们初始化。使⽤这种技巧要注意两个点：

i. 辅助结点⾥⾯的值要「保证后续填表是正确的」；
ii. 「下标的映射关系」。
好了，相信到这里大家还是一头雾水，下面我来展开讲讲
- 有关辅助节点，如果放在这一题来看的话，请问我们的dp[0][0]怎么算呢？
- 因此在本题中，我们需要「添加⼀⾏」，并且「添加⼀列」来避免上述越界情况的发生
- 因此就有了第一点，我们的辅助节点中保存的值，必须保证对我们的题目的解答没有影响，比如在这个题需将 dp[0][1] （或者dp[1][0]）的位置初始化为1 ，剩下创建的值初始化为0，这样就能保证dp[1][1]位置的初始化
- 那么为什么从dp[1][1] 开始呢？我们的辅助队列相当于在最上后最右的位置帮我们又创建了一行一列来初始化，此时机器人所处的位置就变为了dp[1][1]了
- 有关第二点，我们加了一行一列，下标的初始位就不再是dp[0][0]了，因此我们最后返回的值也不是dp[m-1][n-1]而是dp[m][n].。在这个题中下标的映射没啥太大的影响，具体的细节我们放在下个题再讨论

填表顺序：

根据状态转移⽅程和题目分析的推导来看，填表的顺序就是「从上往下」填每⼀⾏，在填写每⼀⾏的时候「从左往右」填每一列

返回值

上面在辅助节点已经说过了，返回值为dp[m][n]

完成上面的算法原理分析，下面我们来具体写一下代码

3 编写代码

class Solution {
public:
    int uniquePaths(int m, int n) {
    	//开辟m*n的dp表
        vector<vector<int>>dp(m+1);
       
        for(int i=0;i<dp.size();i++)
        {
            dp[i].resize(n+1,0);
        }
        dp[0][1]=1;//初始化
        //状态转移方程
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
        return dp[m][n];
    }
};

在这里插入图片描述

照这上面讲的算法原理一步一步照搬挺容易ac的，这里就不细讲了，重点还是放在下面这个题上

二下降路径最小和

原题leetcode链接在这里下降路径最小和

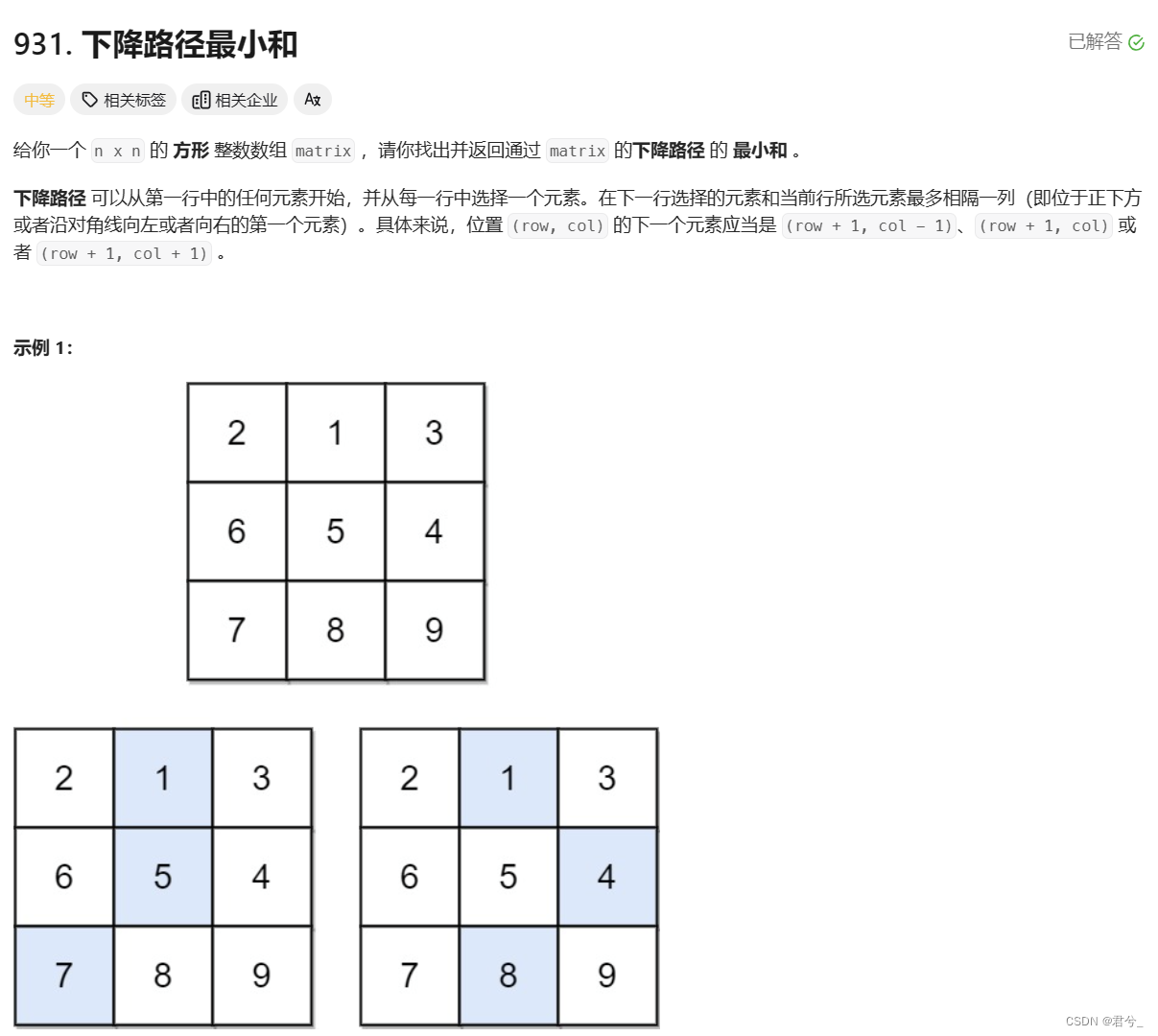
1 题目解析

给你一个 n x n 的方形整数数组 matrix ，请你找出并返回通过 matrix 的下降路径的最小和。
下降路径可以从第一行中的任何元素开始，并从每一行中选择一个元素在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

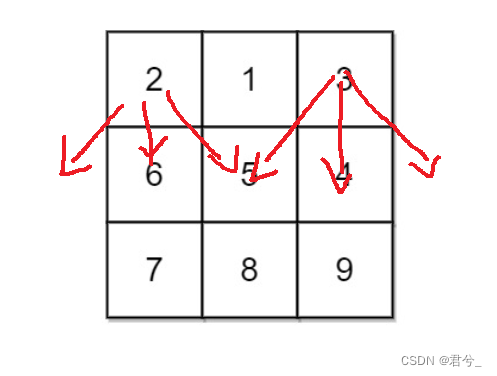
在这里插入图片描述

对于两边的特殊情况，只有向右和向左可供移动

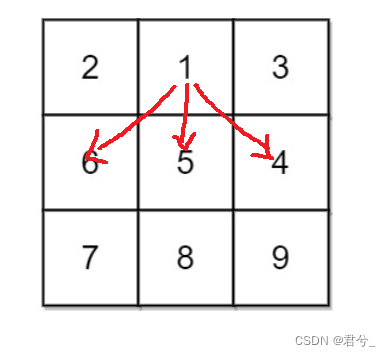
在这里插入图片描述

只有中间的情况，下一行三个位置均可插入

2 算法原理

一看到这种路径算不同种数啊，算最短呐，首先我们要有使用动态规划的想法

状态表示

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：
i. 从 [i, j] 位置出发，到达⽬标位置有多少种⽅式；
ii. 从起始位置出发，到达[i, j] 位置，⼀共有多少种⽅式
这⾥选择第⼆种定义状态表⽰的⽅式：
dp[i][j] 表示：到达[i, j] 位置时，所有下降路径中的最小和
路径问题的状态表示都是类似的，这里就不多阐释了，自己写的时候记得结合一下dp表中存的值符合题目要求就行

状态转移方程

先不考虑越界情况，对于普遍位置的dp[i, j] ，根据题意得，到达[i, j] 位置可能有三种情况：
i. 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置；
ii. 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置；
iii. 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置；
我们要的是三种情况下的「最⼩值」，然后再加上数组中在 [i, j] 位置的值。
于是，我们可以得出状态转移方程
dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +1])) + matrix[i][j]

初始化

从我在题意分析中画的那个图，可以明显看出每一行的最左位置和最右位置都存在越界，因此为了防止出现这种情况，我们还是采用上面讲的辅助节点的方法来进行初始化，不同的是，此时两边都存在可能越界，因此我们要初始化一行两列，示意图如下：
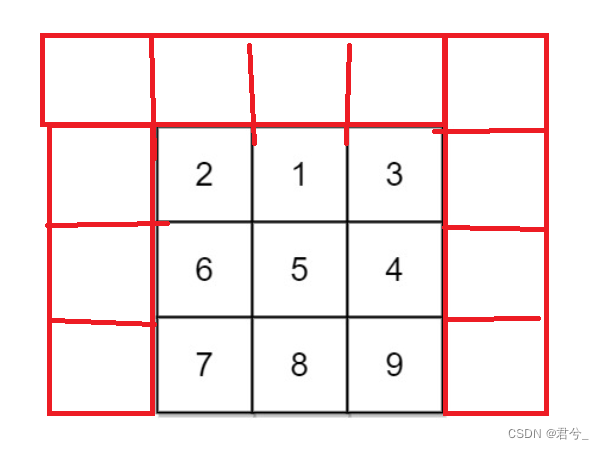
在这里对辅助节点进行初始化时，我们由于是求最小下降路径，为了不影响原dp表结果，此时先把辅助节点都填上一个较大的值。
此时，如果我们全都是较大的值，那么此时dp表第一行的初始化就会直接以这个较大值进行初始化，为了避免这种情况发生，我们将辅助节点的第一行全部初始化为0。

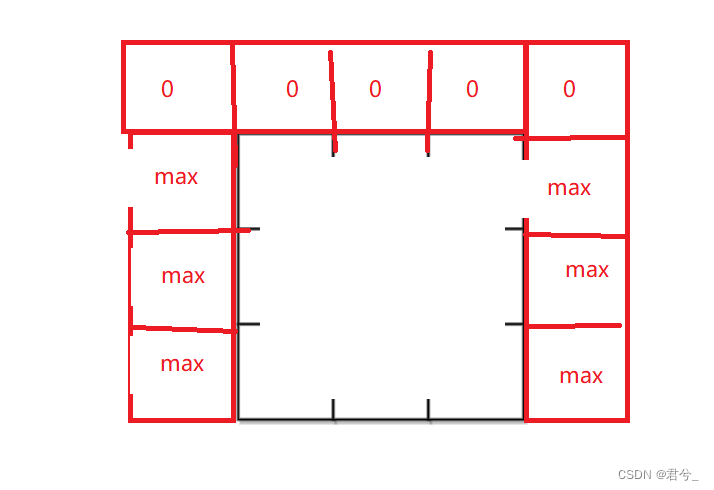
注意，重点来了：
我们之前在辅助节点初始化方法中说过要注意下标的映射关系。
这里，我们需要把原数组的值填入到当前这个dp表中，但是现在的dp表多了一行两列，因此我们之前dp[i][j]=min+matrix[i][j]就需要改成dp[i][j]=min+matrix[i-1][j-1] ，这样才能满足对应的下标关系

填表顺序

题目已经明确告诉你了。从上到下

返回值

注意这⾥不是返回 dp[m][n] 的值！
题⽬要求「只要到达最后⼀⾏」就⾏了，因此这⾥应该返回「dp表中最后⼀⾏的最⼩值」

3 编写代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int n=matrix.size();
        //创建dp表
        vector<vector<int>>dp(n+1,vector<int>(n+2));
        
        //初始化
        for(int i=1;i<=n;i++)
        {
            dp[i][0]=dp[i][n+1]=999999;
        }
        
        //填dp表
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                //状态转移方程
                int ret=min(dp[i-1][j],min(dp[i-1][j+1],dp[i-1][j-1]));
               //之前的值加上此时这里数组的值
                dp[i][j]=ret+matrix[i-1][j-1];
               
            }
        }
        //找最后一行的最小值
        int min1=dp[n][1];
        for(int i=2;i<=n;i++)
        {
           if(dp[n][i]<min1)
           min1=dp[n][i];
              
        }
        return min1;

    }
};