目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
暂无。。。
2 模板
暂无。。。
3 工程化
题目1:求a~b中数字0、数字1、…、数字9出现的次数。
思路:先计算1~a中每位数字出现的次数,然后计算1~b-1中每位数字出现的次数,两个相减即是最终答案。
那么,如何计算1~a中每位数字出现的次数呢?
首先,将a的每一位存入向量num中,例如a=1234567,那么num为,

考虑如下两个子问题,
- 1~a中数字0出现的次数。
- 1~a中数字5出现的次数。为啥选择数字5呢?因为1到9中的任意一个数都和5等价。
对于问题1:1~x中数字0出现的次数。
记num中有n位,从第0位不考虑,因为第0位不可能取到0,即数字首位不能为0,例如0123,这样的数字是不合法的,应该表示成123。所以i从1到n-1,即for (int i = 1; i < n; ++i)。考虑如下情况,
-
当num的第i位取0且其左侧部分不取L时,有多少个数?

左边部分的方案数为:1~L-1,共L-1个数。
右边部分的方案数为:0~ 1 0 n − 1 − i − 1 10^{n-1-i}-1 10n−1−i−1,共 1 0 n − 1 − i 10^{n-1-i} 10n−1−i个数。
故总方案数为: ( L − 1 ) ⋅ 1 0 n − 1 − i (L-1)\cdot 10^{n-1-i} (L−1)⋅10n−1−i。 -
当num的第i位取0且其左侧部分取L时,
2.1 如果第i位原先数字等于0,那么左边方案数=1,右边方案数=0~R,共R+1个,总方案数=1 * (R+1) = R+1。
2.2 如果第i位原先数字大于0,那么左边方案数=1,右边方案数=0~ 1 0 n − 1 − i − 1 10^{n-1-i}-1 10n−1−i−1,共 1 0 n − 1 − i 10^{n-1-i} 10n−1−i个数。
对于问题2:1~x中数字5出现的次数。
如果num的第0位等于5,有R+1个方案数。如果num的第0位大于5,有 1 0 n − 1 10^{n-1} 10n−1个数。
i从1到n-1,即for (int i = 1; i < n; ++i)。考虑如下情况,
-
当num的第i位取5且其左侧部分不取L时,有多少个数?

左边部分的方案数为:0~L-1,共L个数。
右边部分的方案数为:0~ 1 0 n − 1 − i − 1 10^{n-1-i}-1 10n−1−i−1,共 1 0 n − 1 − i 10^{n-1-i} 10n−1−i个数。
故总方案数为: L ⋅ 1 0 n − 1 − i L\cdot 10^{n-1-i} L⋅10n−1−i。 -
当num的第i位取5且其左侧部分取L时,
2.1 如果第i位原先数字等于5,那么左边方案数=1,右边方案数=0~R,共R+1个,总方案数=1 * (R+1) = R+1。
2.2 如果第i位原先数字大于5,那么左边方案数=1,右边方案数=0~ 1 0 n − 1 − i − 1 10^{n-1-i}-1 10n−1−i−1,共 1 0 n − 1 − i 10^{n-1-i} 10n−1−i个数。
综合上述,C++代码如下,
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
int a, b;
int compute_R(const vector<int>& num, int i) {//计算第i位右侧数字大小
int R = 0;
for (int k = i + 1; k < num.size(); ++k) {
R = R * 10 + num[k];
}
return R;
}
int compute_L(const vector<int>& num, int i) {//计算第i位左侧数字大小
int L = 0;
for (int k = 0; k < i; ++k) {
L = L * 10 + num[k];
}
return L;
}
int compute_cnt(int a, int x) {//计算1~a中x出现的次数
if (a <= 0) return 0;
vector<int> num; //把a转化为num,高位在前
int t = a;
while (t) {
num.emplace_back(t % 10);
t /= 10;
}
reverse(num.begin(), num.end()); //保证高位在前
int n = num.size(); //a总共有n位
int res = 0; //存储1~a中x出现的次数
//考虑第0位取x的情况
if (x != 0) {
if (num[0] == x) {
//有R+1个方案
int R = compute_R(num, 0);
res += R + 1;
} else if (num[0] > x) {
//有10^(n-1)个方案数
res += pow(10, n - 1);
}
}
//考虑第i位取x的情况
for (int i = 1; i < n; ++i) {
//计算情况1中x出现的次数
if (x == 0) {
int L = compute_L(num, i);
res += (L - 1) * pow(10, n - 1 - i);
} else {
int L = compute_L(num, i);
res += L * pow(10, n - 1 - i);
}
//计算情况2中x出现的次数
if (num[i] == x) {
int R = compute_R(num, i);
res += R + 1;
} else if (num[i] > x) {
res += pow(10, n - 1 - i);
}
}
return res;//返回1~a中x出现的次数
}
int main() {
while (cin >> a >> b, a || b) {
if (a > b) swap(a, b); //保证b是大数
for (int x = 0; x < 10; ++x) {
int cnt1 = compute_cnt(b, x); //计算1~b中x出现的次数
int cnt2 = compute_cnt(a - 1, x); //计算1~a中x出现的次数
cout << cnt1 - cnt2 << " ";
}
cout << endl;
}
return 0;
}
题目2:在N * M的棋盘下,摆放1*2的矩形块,可以竖着摆,也可以横着摆,要求摆满棋盘,求有多少种摆放方案。
解题思路:状态压缩类DP。
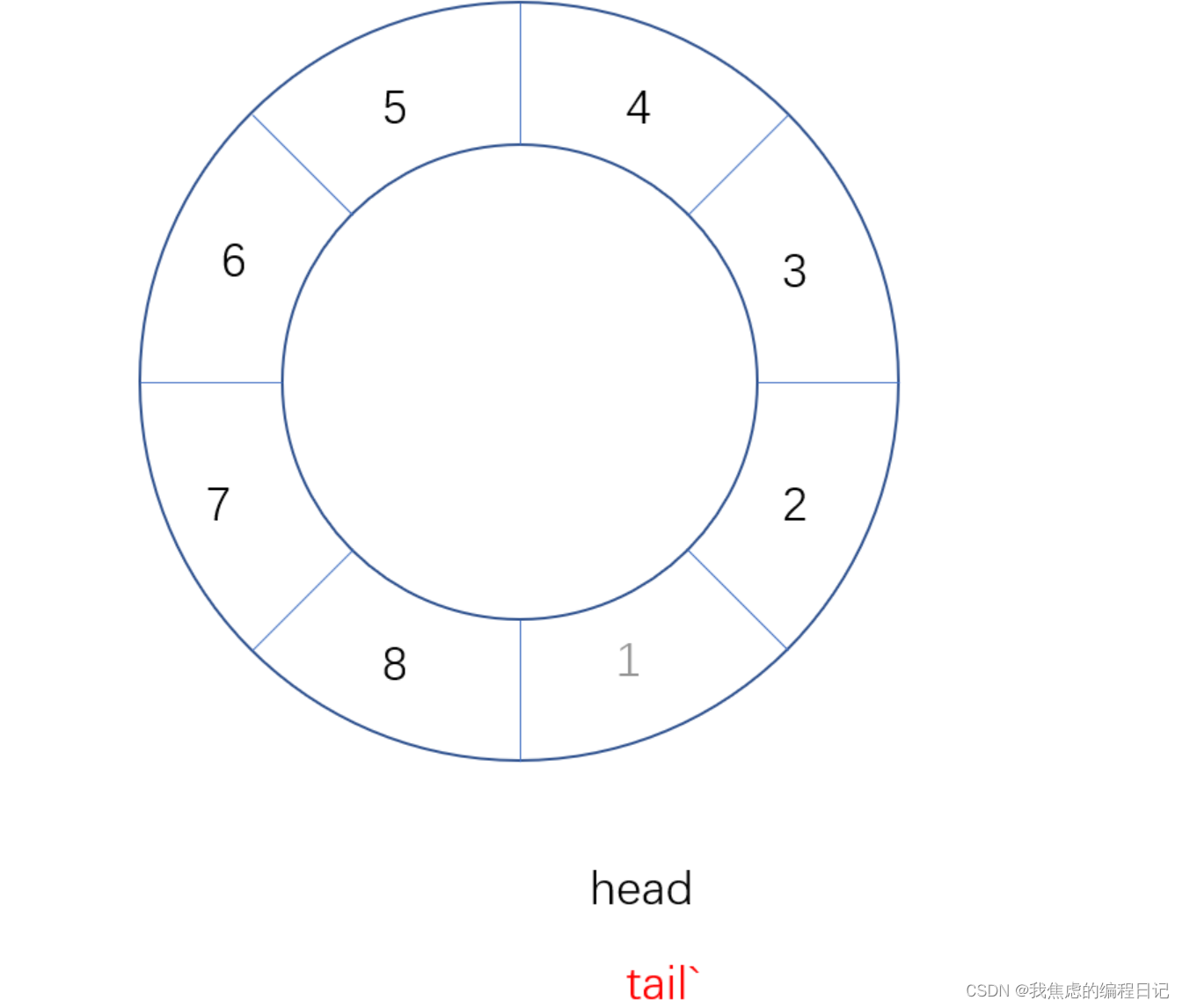
规定横着摆放的1*2的矩形块,第一个小方格为起点方格,第二个小方格为终点方格,如下图所示,

f[i][j]状态定义:前i-1列已经摆放完毕,第i列中终点方格的状态为j,的方案数。
其中终点方格的状态j是指,从第0行到第n-1行,有终点网格的记作1,没有终点网格的记作0。比如下图中第1列的终点方格的状态是 ( 1001 ) 2 (1001)_2 (1001)2,即十进制中的9。

f[i][j]的状态转移:f[i-1][k],即前i-2列已经摆放完毕,第i-1列中终点网格的状态为k。k需要满足两个条件:
- 第i-1列中的终点网格和起点网格不能重合,其中终点网格的状态为k,起点网格的状态为j,也即
k & j == 0。 - 连续的空网格的数目不能是奇数,否则竖着摆放不下1*2的矩形块。即数
k | j二进制表示中连续0的数目不能是奇数。
故,综合上述,状态转移方程为,
f
[
i
]
[
j
]
=
∑
k
f
[
i
−
1
]
[
k
]
f[i][j] = \sum_kf[i-1][k]
f[i][j]=k∑f[i−1][k]
初始化f[0][0] = 1。
最终答案f[M][0],也即第0列、第1列、…、第M-1列均摆放完毕,第M列中终点格子的状态为0的方案数。
C++代码如下,
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
const int N = 12, M = 1 << N;
bool st[M];
vector<vector<int>> last(M);
long long f[N][M];
int n, m;
int main() {
while (cin >> n >> m, n || m) {
//n*m的棋盘
//步骤1:把状态0~1<<n-1中满足连续0个数为偶数的状态标识出来
memset(st, 0, sizeof st); //多组测试数据,所以要初始化
for (int i = 0; i < 1 << n; ++i) {
//数i的二进制表示中,连续0的个数是不是都是偶数
bool flag = true;
int cnt = 0; //连续0的个数
for (int j = 0; j < n; ++j) {
if (i >> j & 1) {//第j位为1,前面的连续0之和为cnt
if (cnt & 1) {//如果cnt是奇数
flag = false;
break;
}
cnt = 0;
} else {
cnt += 1;
}
}
if (cnt & 1) flag = false;//判断最后一个连续0的数目
st[i] = flag; //true表示状态i中连续0的个数都是偶数。
//cout << "i = " << i << ", st[i] = " << st[i] << endl;
}
//步骤2:f[i][j]和f[i-1][k],存储j满足要求的k
for (int j = 0; j < 1 << n; ++j) {
last[j].clear(); //多组测试数据,所以要清空
for (int k = 0; k < 1 << n; ++k) {
if ((k & j) == 0 && st[k | j]) {
last[j].emplace_back(k);
}
}
}
//步骤3:正式dp
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; ++i) {
for (int j = 0; j < 1 << n; ++j) {
for (auto k : last[j]) {
f[i][j] += f[i-1][k];
}
}
}
cout << f[m][0] << endl;
}
return 0;
}
题目3:给定n*n的矩阵,表示n个结点两两之间的距离,求从0号结点出发到达第n-1号结点,经过每一个结点一次的路径的最小距离。
解题思路:状态压缩DP。
状态定义,f[i][j],即:所有从第0号结点走到第j号结点,且走过的结点是i的路径,的最小值。
其中i的二进制表示中第0位为1表示,经过第0号结点,否则不经过第0号结点。
i的二进制表示中第1位为1表示,经过第1号结点,否则不经过第1号结点。
i的二进制表示中第2位为1表示,经过第2号结点,否则不经过第2号结点。
……
i的二进制表示中第n-1位为1表示,经过第n-1号结点,否则不经过第n-1号结点。
注意,只有满足(i & 1) == 1 && (i & (1 << j)) == (1 << j)时,状态f[i][j]才合法。
状态转移,考虑最后一步咋走的,即f[last][k] + d[k][j],其中i包含结点k时才合法,即(i & (1 << k)) == (1 << k),且last = i - (1 << j)。
故,综合上述,状态转移方程为,
f
[
i
]
[
j
]
=
m
i
n
k
{
f
[
l
a
s
t
]
[
k
]
+
d
[
k
]
[
j
]
}
f[i][j] = \underset {k}{min} \{ f[last][k] + d[k][j] \}
f[i][j]=kmin{f[last][k]+d[k][j]}
l
a
s
t
=
i
−
(
1
<
<
k
)
last = i - (1 << k)
last=i−(1<<k)
初始化,f[1][0] = 0,其余初始化为正无穷大。
最终答案,f[(1 << n) - 1][n-1]。
C++代码如下,
#include <iostream>
#include <cstring>
using namespace std;
const int N = 21, M = 1 << N;
int f[M][N];
int n;
int d[N][N];
int main() {
cin >> n;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
cin >> d[i][j];
}
}
memset(f, 0x3f, sizeof f);
f[1][0] = 0;
for (int i = 0; i < (1 << n); ++i) {
for (int j = 0; j < n; ++j) {
//从0出发到达j,经过的结点是i
if ((i & 1) == 1 && (i & (1 << j)) == (1 << j)) {
//f[i][j]是合法的
for (int k = 0; k < n; ++k) {
if ((i & (1 << k)) == (1 << k)) {
//i中有k
int last = i - (1 << j);
f[i][j] = min(f[i][j], f[last][k] + d[k][j]);
}
}
}
}
}
cout << f[(1 << n) - 1][n-1] << endl;
return 0;
}
题目4:没有上司的舞会。直接上司和员工不能同时选择,求最大值。
解题思路:树形DP,从根结点递归处理。
状态定义,有,
f[i][0],所有以i为根的子树中选择,但不选择结点i的方案数中的最大值。f[i][1],所有以i为根的子树中选择,且选择结点i的方案数中的最大值。
状态转移,
f
[
i
]
[
0
]
=
∑
j
m
a
x
{
f
[
j
]
[
0
]
,
f
[
j
]
[
1
]
}
f[i][0] = \sum_j max\{ f[j][0], f[j][1] \}
f[i][0]=j∑max{f[j][0],f[j][1]}
其中结点j为结点i的子结点。
f
[
i
]
[
1
]
=
w
[
i
]
+
∑
j
f
[
j
]
[
0
]
f[i][1] = w[i] + \sum_j f[j][0]
f[i][1]=w[i]+j∑f[j][0]
其中结点j为结点i的子结点。
初始化,二维数组初始化为0。
记根结点为start,那么最终答案res = max(f[start][0], f[start][1])。
C++代码为,
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
const int N = 6010;
int n, start;
bool has_father[N];
int happy[N];
int f[N][2];
vector<vector<int>> sons(N);
void dfs(int i) {
f[i][1] = happy[i];
for (auto j : sons[i]) {
dfs(j);
f[i][1] += f[j][0];
f[i][0] += max(f[j][0], f[j][1]);
}
return;
}
int main() {
cin >> n;
for (int i = 1; i <= n; ++i) cin >> happy[i];
for (int i = 1; i < n; ++i) {
int a, b;
cin >> a >> b;
has_father[a] = true;
sons[b].emplace_back(a);
}
//找到根结点
start = -1;
for (int i = 1; i <= n; ++i) {
if (has_father[i] == false) {
start = i;
break;
}
}
dfs(start);
cout << max(f[start][0], f[start][1]) << endl;
return 0;
}
题目5:滑雪。n*m的网格,可以往上下左右方向尝试,只能从高处滑到低处。求路径最长值。
思路:记忆化搜索,状态先全部初始化为-1,然后递归每一个位置,如果f[i][j] != -1,则说明它被计算过了,直接返回。
状态表示,f[i][j]:从(i,j)开始滑的最长路径值。
状态转移,有:
- 如果能往上滑,即(i-1,j)在网格内且
h[i][j] > h[i-1][j],有f[i-1][j] + 1。 - 如果能往下滑,即(i+1,j)在网格内且
h[i][j] > h[i+1][j],有f[i+1][j] + 1。 - 如果能往左滑,即(i-1,j)在网格内且
h[i][j] > h[i-1][j],有f[i-1][j] + 1。 - 如果能往右滑,即(i+1,j)在网格内且
h[i][j] > h[i+1][j],有f[i+1][j] + 1。
初始化,所有状态均设置为-1。
答案,即所有状态的最大值。
C++代码如下,
#include <iostream>
#include <cstring>
using namespace std;
const int N = 310;
int n, m;
int f[N][N], h[N][N];
int dirs[4][2] = {{1,0}, {-1,0}, {0,1}, {0,-1}};
int dfs(int i, int j) {
if (f[i][j] != -1) return f[i][j];
f[i][j] = 1;
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k][0], y = j + dirs[k][1];
if (x >= 1 && x <= n && y >= 1 && y <= m && h[i][j] > h[x][y]) {
f[i][j] = max(f[i][j], dfs(x, y) + 1);
}
}
return f[i][j];
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
cin >> h[i][j];
}
}
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
res = max(res, dfs(i, j));
}
}
cout << res << endl;
return 0;
}