#pic_center

$R_1$

$R^2$

知识框架

No.1 自注意力机制(self-attention)

• 接下来我们将探讨另一个常见的网络架构——自注意力（self-attention）。自注意力的提出旨在解决什么问题呢？让我们深入了解。

一、输入的种类以及表示

1、输入是a vector

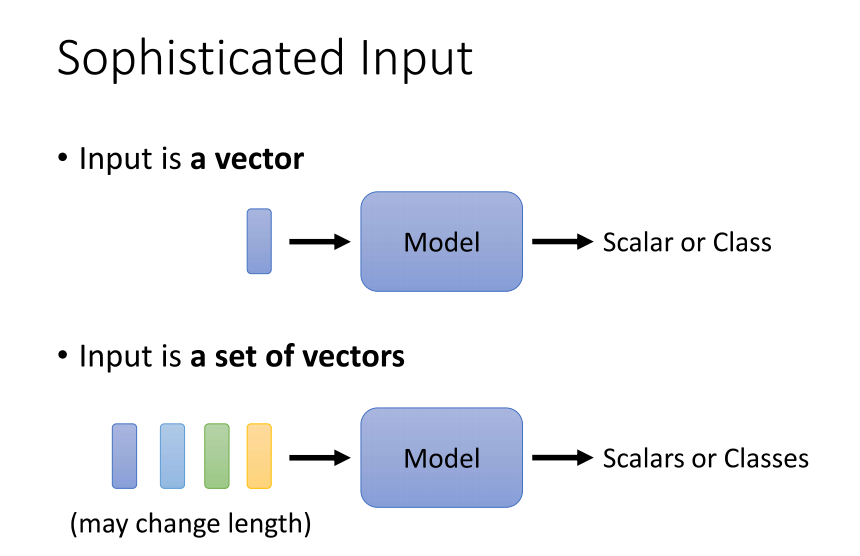
• 解决的问题是到目前为止，我们的network input都是一个向量。无论是在预测YouTube观看人数的问题上，还是在影像处理领域，我们的输入都是一个向量。然后，我们的输出可能是一个数值，属于回归问题，或者是一个类别，涉及到分类问题。
• 然而，假设我们面对更加复杂的情境呢？假设我们的输入是一排向量呢？，而且这些向量的数量是会变化的呢？在先前讨论影像处理时，我们强调过假设输入的影像大小都是相同的。但是，那现在假设我们的输入会不一样呢？每次我们的模型输入的sequence数目和sequence长度都可能不同，我们应该如何处理呢？有没有一些例子，其中输入是一个序列，而且序列的长度会发生变化的呢？

2、输入是a set of vectors(一段文字)

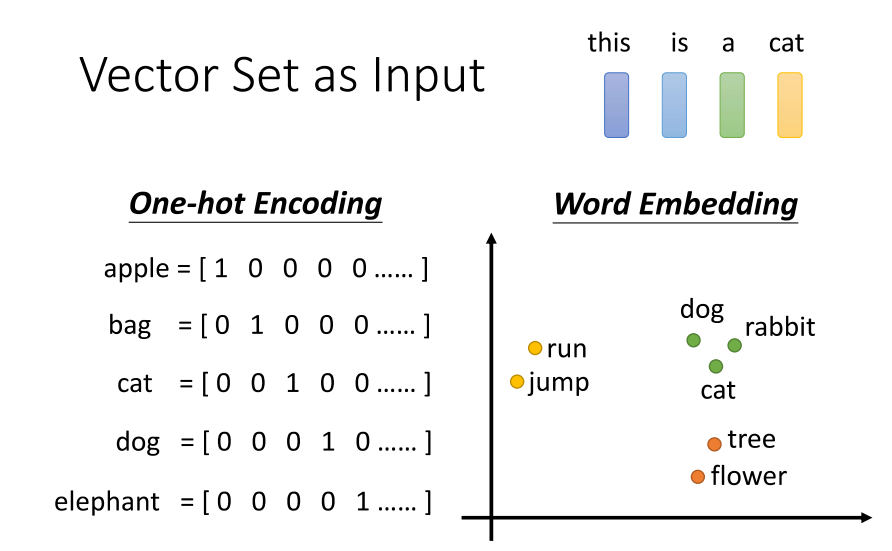
• 第一个例子涉及到文字处理。假设我们今天要处理网络输入，输入是一个句子。每个句子的长度都不相同，每个句子中的词汇数量也不同。如果我们将句子中的每个词汇都描述为一个向量，用向量表示的话，那我们模型的输入就会是一个Vector set，而且这个Vector set的大小每次都不一样，因为句子长度不同，导致Vector set的大小也不同。
• 那么如何将一个词汇表示成一个向量呢？简单来说，最简单的做法是使用单热编码（one-hot encoding）。你可以想象开一个很长的向量，这个向量的长度与世界上存在的词汇数目一样多。假设英文有10万个词汇，那就开一个10万维的向量，每一个维度对应一个词汇，例如“apple”就是100、"bag"就是010、"cat"就是001，以此类推。
• 然而，这样的表示方法有一个非常严重的问题，即假设所有的词汇彼此之间都是没有关系的。从这个向量里面，你看不到词汇之间的关联，比如"cat"和"dog"都是动物，它们应该更接近；"cat"和"apple"一个是动物，一个是植物，它们应该更不相像。这个向量里面没有任何关于语义关系的信息。
• 另外一个方法是词嵌入（word embeddings），我们会给每一个词汇一个向量，而这个向量是包含了语义信息的。如果你将词嵌入可视化，你会发现所有的动物可能聚集成一团，所有的植物可能聚集成一团，所有的动词可能聚集成一团，等等。至于词嵌入是如何得到的，如果你感兴趣，可以查阅相关资料。总之，在网络上你可以找到一种叫做词嵌入的方法，它会为每一个词汇创建一个向量，而一个句子就是一排长度不一的向量。

3、输入是a set of vectors(一段音频)

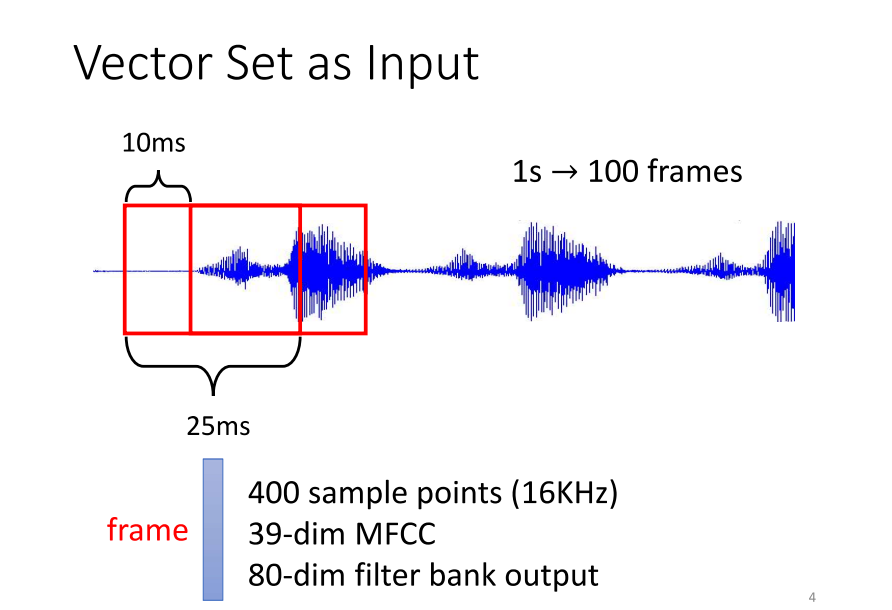
• 还有哪些例子需要将一个向量的sequence作为输入呢？举例来说，中的一个任务是处理一段声音信号，实际上就是一系列向量的序列。具体来说，我们会将一段声音信号取一个范围，这个范围被称为一个窗口（window）。窗口中的信息会被描述成一个向量，这个向量被称为一个帧（frame）。在语音领域，我们通常将一个向量称为一个帧。刚好，这个窗口的长度是25毫秒。
• 那么，如何将这样一个小段的声音信号转换成一个帧，变成一个向量呢？这里有各种各样的方法，具体的细节这里就不展开讨论了，因为有许多不同的方法可以用一个向量来描述25毫秒内的语音信号。接着，为了描述整段声音信号，我们会将这个窗口向右移动一些距离，通常是10毫秒。有人可能会问为什么窗口长度是25，移动的距离是10，这个问题其实很难回答。这是由古圣先贤调试得到的最佳结果，调整这些参数自己很难得到好的效果。
• 总之，一段声音信号就是用一串向量来表示的。由于每个窗口向右移动10毫秒，所以一秒钟的声音信号有多少个向量呢？有100个。因此，一分钟的声音信号就有6000个向量。语音信号实际上是一个复杂的一小段声音信号，其中包含的信息量非常可观。所以，声音信号就是一系列向量的集合。那还有哪些其他东西也是一系列向量的集合呢？

4、输入是a set of vectors(一段图谱)

• 一个图，也就是一个graph，实际上是一组节点之间相互关联的集合。在计算机科学中，我们常常遇到社交网络这样的图。在社交网络中，每个节点代表一个个体，通常是一个人，而节点之间的边则表示它们之间的关系，比如是否是朋友等。每个节点可以被看作是一个向量，这个向量可以包含个体的各种信息，比如性别、年龄、职业、言论等。通过使用向量来表示这些信息，我们可以将整个社交网络看作是一组向量的集合。
• 那么，还有哪些例子与图相关呢？在计算机科学中，图是一种通用的数据结构，因此与图有关的例子非常丰富。例如，推荐系统中的用户-物品关系图，网络拓扑结构中的节点和连接关系，或者是任务调度中的依赖关系图等都可以被看作是图的应用。在这些例子中，图的概念被广泛用于建模和解决各种计算机科学问题。

5、输入是a set of vectors(一个分子)

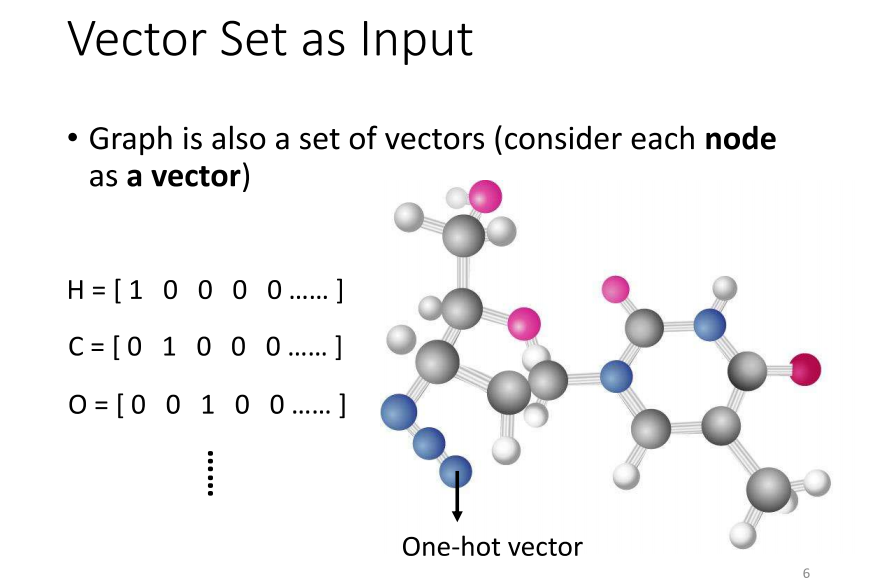
• 首先，我们谈谈分子的概念，它在计算机科学中也可以被视为一种图。现在，像药物发现这样的应用在Covid-19疫情期间变得非常重要。许多人期待着，通过机器学习，我们能在药物发现领域取得突破。在这个时候，你需要将一个分子作为你模型的输入。一个分子可以被视为一个图，其中分子上的每个球代表一个原子，就像图中的节点一样。
• 那么，一个原子如何用向量表示呢？你可以使用二进制向量表示，例如，用one-hot vector表示。比如说，氢可以用1000表示，碳可以用0100表示，氧可以用0010表示。这样，每个原子都可以用一个向量来表示。一个分子就是一组这样的向量的集合，构成了一个图。这个图可以被用于机器学习模型的输入，特别是在药物发现等领域。

二、输出的种类以及表示

1、第一种可能的输出

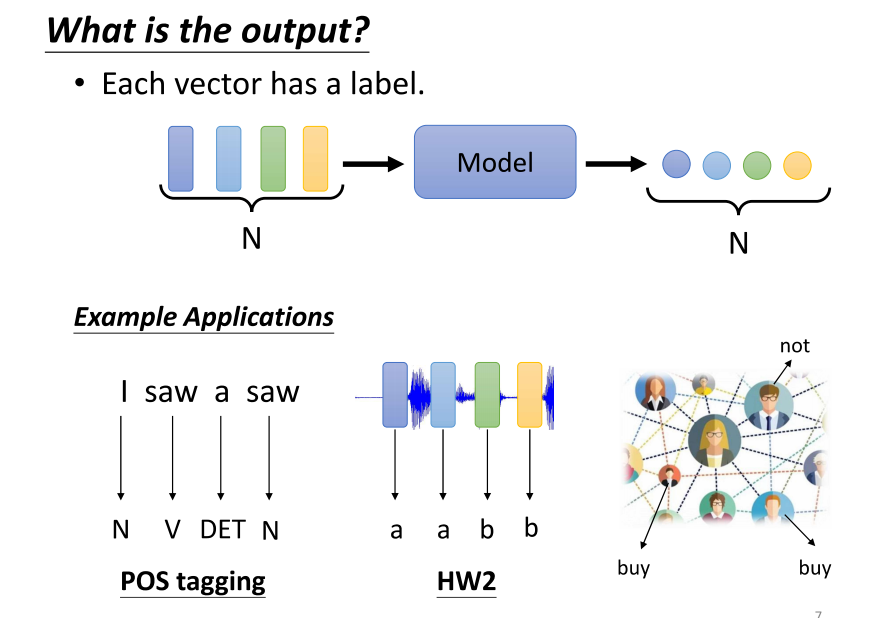
• 那么，输出是什么呢？刚才提到，输入可以是一组向量，可以是文字、语音或图。在这种情况下，我们可能有三种输出的可能性。第一种可能性是，每个向量都有一个对应的标签，也就是说，当模型看到输入是四个向量时，它需要输出4个标签。每个标签可能是一个数值，这就是回归问题；如果每个标签是一个类别，那就是分类问题。在第一种可能性中，输入和输出的长度是相同的，模型无需担心输出多少的标签，与输入向量的数量保持一致。例如，在文字处理领域，如果要进行词性标注（POS tagging），这就是一个应用第一种输出类型的任务。
• 举例来说，对于POS tagging，我们想要让机器自动确定每个词汇的词性，比如名词、动词、形容词等。这个任务并不容易，因为一个词汇可能在不同上下文中有不同的词性。例如，句子"I saw a saw"中的第二个"saw"在名词用法时表示句子，而不是sentence。机器需要理解每个输入词汇的具体词性，第一个saw是动词，第二个是名词，这就是一种输入和输出长度相同的任务。
• 对于语音任务，我们也是面对着第一种可能性的输出。在语音任务中，我们可能需要决定每个音频向量对应的音素（phoning），这相当于音标的简化版本。如果是社交网络领域，我们给定一个图，模型需要决定每个节点的特性，比如他们是否可能购买某个商品，以便做出个性化的推荐。
• 综上所述，这就是一些应用第一种可能性输出的例子，其中输入和输出的数量保持一致。

2、第二种可能的输出

• 第二种可能的输出是什么呢？第二种可能的输出是我们在整个sequence中只需要输出一个标签。举例来说，如果是文字领域，我们可以考虑情感分析（sentiment analysis）。情感分析是什么呢？它是一种让机器阅读一段文本，然后确定这段文本是正面的还是负面的任务。这种应用非常有用，比如当你公司推出了一款新产品，上线后你想知道网友对它的评价，但你不可能逐条分析每个网友的留言。使用情感分析技术，机器可以自动判断一篇帖文中对某个产品的评价是正面还是负面，从而了解产品在用户心中的声誉。这就是情感分析，它在整个句子中只需要一个标签，如"positive"或"negative"。
• 或者，如果涉及到图的情况，你可能想要给定一个分子，然后预测这个分子是否有毒性，或者它的亲水性如何。这就是在给定一个图的情况下输出一个标签的例子，也是第二类输出的一种。
• 这里讨论了第二种可能性的输出，即在整个序列中只需要一个标签。

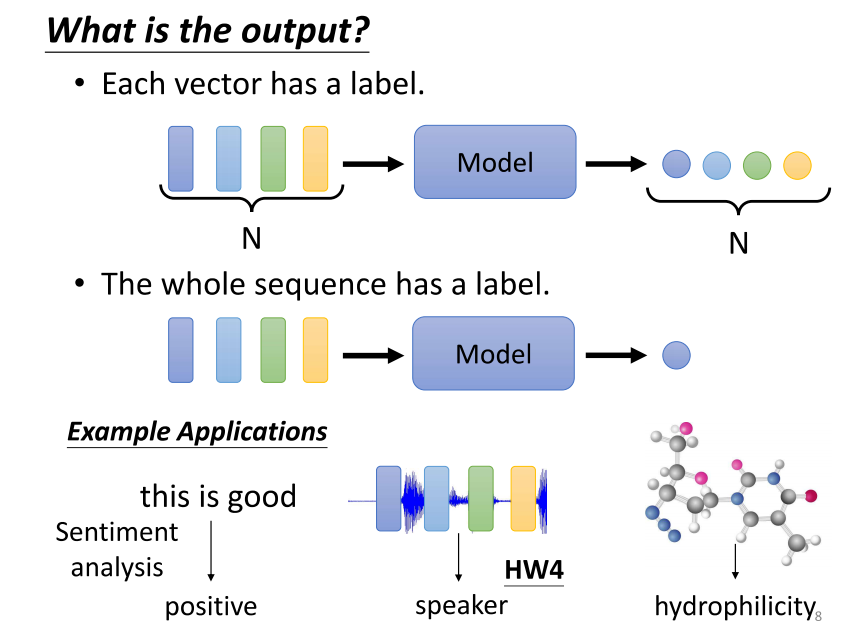
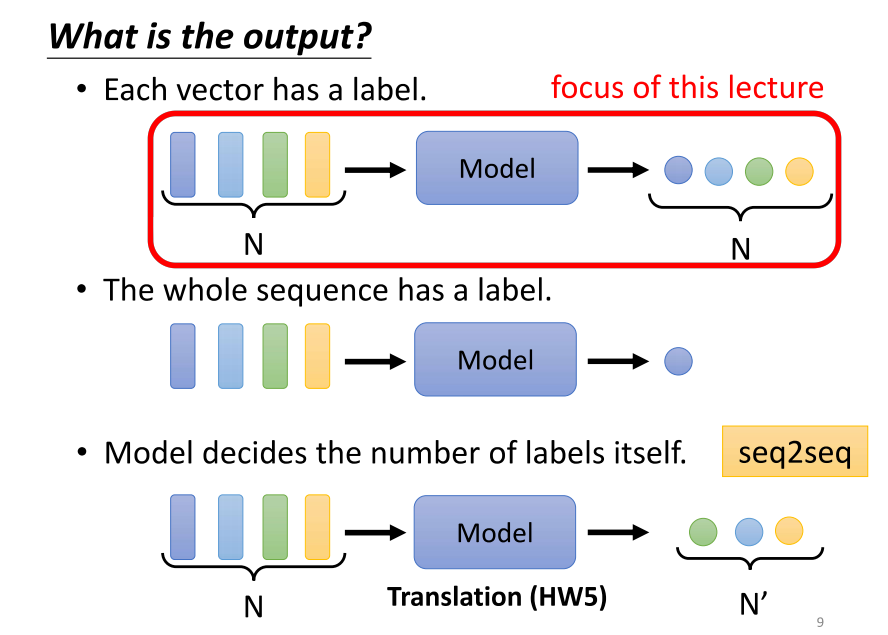
3、第三种可能的输出

• 第三个可能的输出。第三个可能的输出是，我们不确定应该输出多少个标签，机器需要自己决定输出多少个标签。可能你的输入是n个向量，输出可能是n个标签。为什么是n，机器会自己决定。这种任务又被称为序列到序列（sequence to sequence）的任务。
• 涉及到序列到序列的，后续会有更深入的讨论。可以想象，翻译是sequence to sequence任务的一个例子，因为输入和输出是不同的语言，它们的词汇数量本来就可能不一样多。或者，语音辨识也是真正的序列到序列任务，输入是一句话，输出是一段文字。在今天的讨论中，我们仅仅涉及了第一种类型和第二种类型。有关第三种类型的内容，我们将在以后的课程中详细讨论。如果你对第二种类型的问题感兴趣，你可以查看作业室，看看它是如何处理的。由于上课时间有限，今天我们先只讲解了第一个类型，也就是输入和输出数量相同的情况。这种情况被称为序列标注（sequence labeling）。

三、self-attention

1、Sequence Labeling

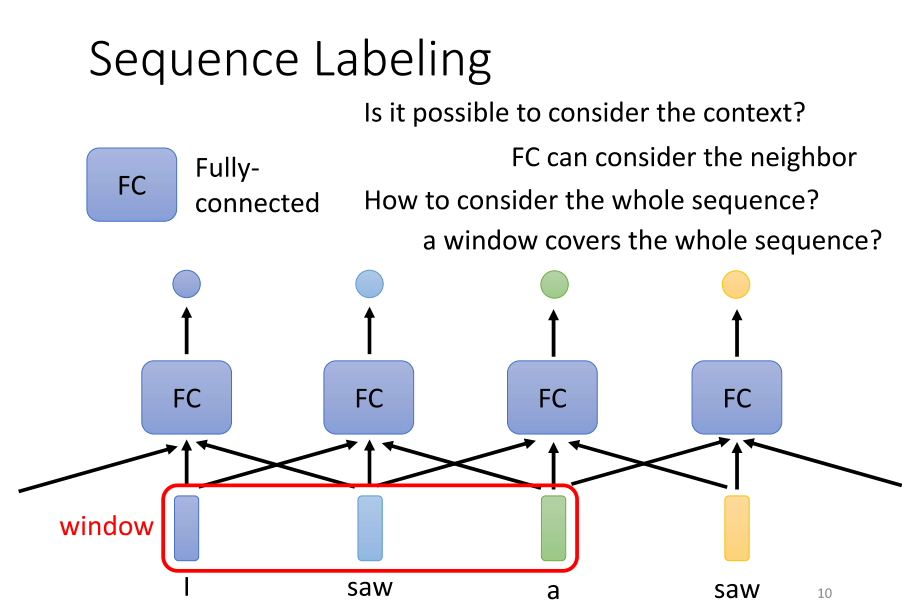
• 每一个向量都分配一个标签。解决Sequence标注问题的方法是使用全连接网络。尽管输入是一个Sequence，我们可以采取分而治之的策略，将每个向量分别输入到全连接网络中。全连接网络将输出给我们，我们需要考虑是回归还是分类任务。然而，这种方法显然存在很大的问题。
• 问题的关键在于，在处理词性标记的任务时，例如给定句子 “I saw a saw”，对于全连接网络而言，第一个 “saw” 与第二个 “saw” 完全相同，它们是相同的词汇。由于全连接网络将相同的输入映射为相同的输出，它无法区分这两个 “saw”。然而，我们期望第一个 “saw” 输出动词，而第二个 “saw” 输出名词。这给全连接网络造成了困扰，因为它无法处理这种情况，使得如何正确输出成为难题。
• 为了解决这个问题，可以让全连接网络考虑更多的上下文信息，例如使用self attention。通过将中的每个向量及其前后几个向量串联起来，并一起输入到全连接网络中，可以在考虑上下文的情况下完成任务。这种方法在作业2中已经被助教采用，通过观察向量前后5个向量的信息，以总共11个向量的信息来确定它所属的音标。因此，给全连接网络提供整个窗口的信息，使其能够考虑相邻向量的上下文信息，但这种方法仍然有一些局限性。
• 对于作业2而言，使用这种方法已经足够好，因为只需考虑前后5个向量就能得到不错的结果。因此，要过强基线，重点不在于考虑整个序列，不必再朝这个方向努力。未来在使用给定数据时，可以轻松地过强基线。
• 然而，真正的问题在于，如果今天有一个任务不是通过考虑一个窗口就可以解决，而是需要考虑整个序列才能解决，那该如何处理呢？有人可能认为开一个大窗口覆盖整个序列是一种容易的方法。但是，不要忘记，序列的长度是各异的。如果我们要确保窗口足够大，以覆盖整个序列，那么可能需要统计训练数据，查看最长的序列有多长，然后开一个比最长序列更长的窗口才能确保覆盖。然而，开这么大的窗口意味着全连接网络需要大量的参数，可能会导致计算量巨大，甚至容易出现过拟合的问题。因此，有没有更好的方法来考虑整个输入序列的信息呢？这就是我们接下来要介绍的self attention的用途。

2、自注意力机制架构

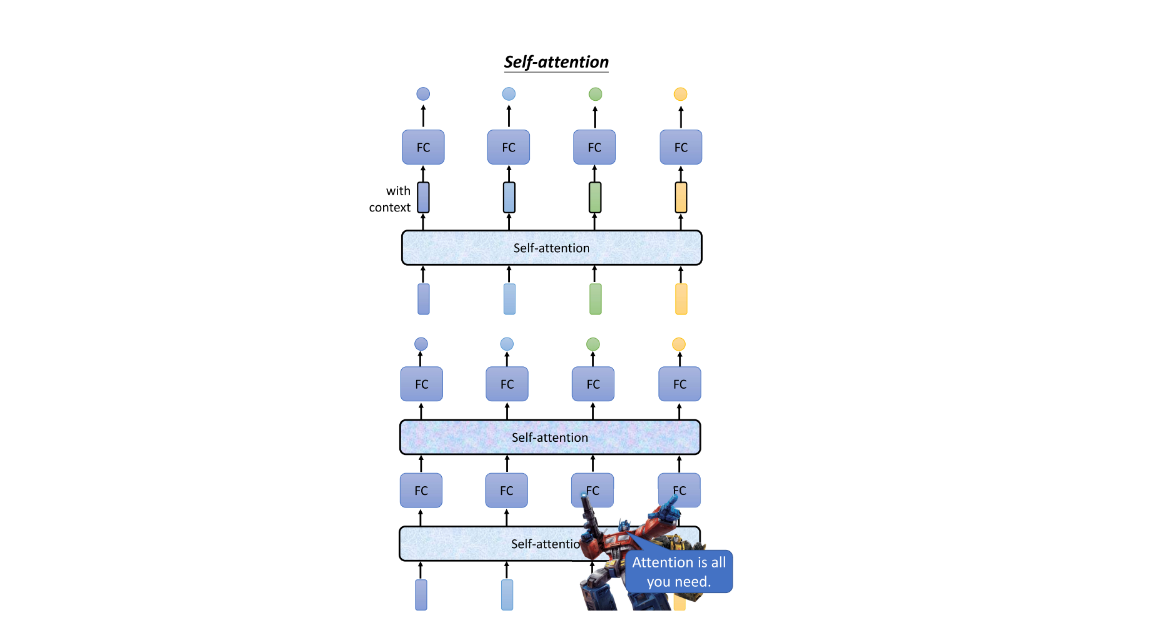
• 那么，self attention是如何运作的呢？self attention的运作方式是吃入整个序列，然后为每个输入的Vector产生一个相应的输出Vector。例如，输入一个深蓝色的Vector，它会输出一个浅蓝色的Vector；输入4个Vector，它就输出4个Vector。这四个Vector的特殊之处在于它们都是在考虑整个序列的情况下生成的。
• 具体而言，每个项量都被赋予一个黑色的框框，表示它不是普通项量，而是在考虑整个句子后得到的信息。然后，将这个考虑了整个句子的项量传递给全连接网络，以确定它应该是什么样的类别或包含什么样的数字。通过这种方法，全连接网络不再只考虑一个小范围或窗口，而是考虑整个序列的信息，从而决定输出的结果。
• self attention并不仅限于使用一次，可以堆叠多次。通过交替使用self attention和全连接网络，可以处理整个序列的信息。在这个过程中，self attention专注于处理整个序列的信息，而全连接网络专注于处理某个位置的信息。这种交替使用的方式使得模型更加灵活。
• 关于self attention，最知名的相关论文之一是《Attention is All You Need》。在这篇论文中，Google提出了Transformer这一网络架构，其中一个最关键的组件就是self attention。Transformer是一个强大的网络，被形象地比喻为变形金刚。self attention被认为是Transformer的核心，而这个模型在自然语言处理等领域取得了巨大成功。
• 需要注意的是，像self attention这样的架构并不是只有在《Attention is All You Need》这篇论文中提出的，还有许多更早的论文提出了类似的思想，只是名称可能不同，例如self mention等。然而，《Attention is All You Need》的出现确实推动了self attention等模型的研究与应用。

3、self-attention的输入输出

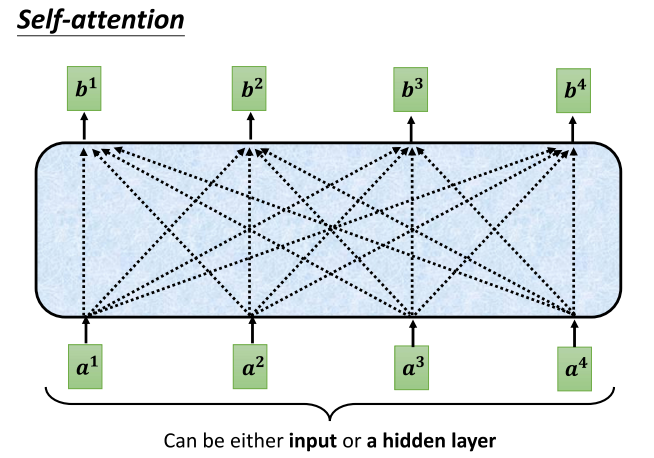
• Attention是如何运作的呢？在attention的输入中，它是一串的Vector。这个Meta（元信息）可能是整个网络的输入，也可能是某个隐藏层的输出。因此，我们这里不使用x来表示它，而是用a来表示它，表示它有可能是前面已经经过一些处理的，是某个隐藏层的输出。当一排a这个项链形成后，
• self attention要关注另外一排b这个项链。在这个项链中，每一个b都是在考虑了所有的a之后才生成的。因此，这里特意画了非常多的箭头，告诉你b1考虑了a1到a4产生的，b2考虑了a1到a4产生的，b3和b4同理，都是考虑了整个输入序列才产生的。

4、self-attention的内部相关性

• 接下来，我们要说明如何生成b1这个项量。一旦你理解了如何生成b1，你就知道如何生成剩下的b项，即b2、b3和b4。那么，如何生成b1呢？
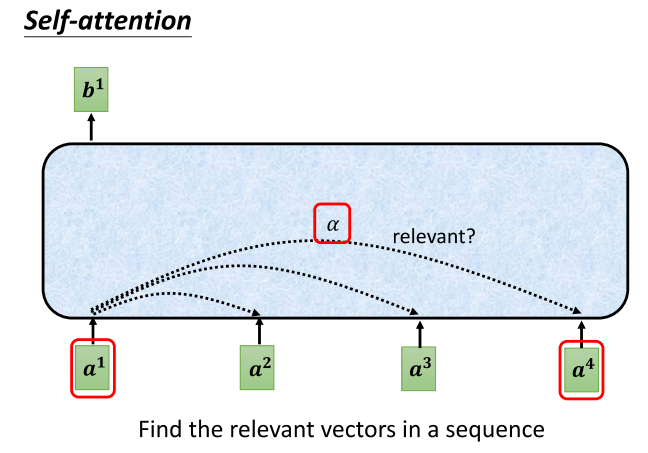
• 首先，我们根据a1，在整个序列中找出与a1相关的其他项链。我们知道，在进行self attention时，我们的目的是为了考虑整个序列，但又不希望将整个序列的所有信息都包含在一个窗口中。因此，我们有一个特殊的机制，根据a1这个项量，找出整个较长序列中哪些部分是重要的，哪些部分与判断a1的类别相关，哪些部分是我们在决定a1的类别或回归数值时所需的信息。
• 每一个向量与a1的关联程度，我们用一个数值α（阿法）来表示。然后，self attention模块如何自动决定两个项量之间的关联性呢？当给定两个项量，比如a1和a4时，它是如何决定a1和a4之间的相关性，并为其分配一个数值α呢？

5、self-attention如何计算α

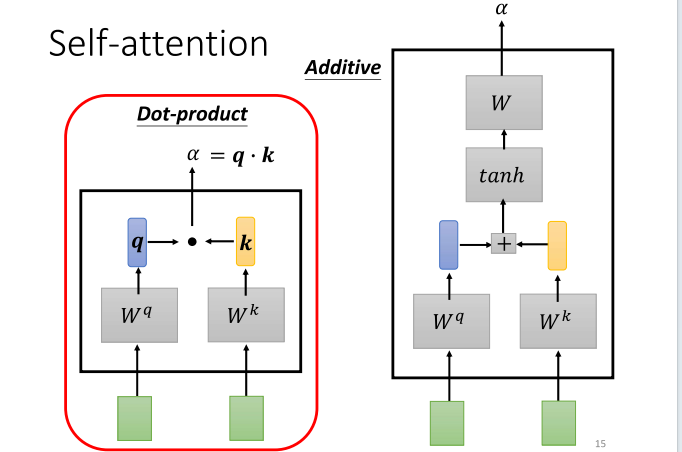
• 若要计算attention，你需要一个用于计算attention的模块。这个模块以两个项量作为输入，然后直接输出（α）这个数值，这个数值可以表示两个项量之间的关联程度。那么，如何计算这个阿法的数值呢？有许多不同的方法，其中比较常见的一种叫做乘加法。在这种方法中，将输入的两个项量分别与两个不同的矩阵相乘，左边的项量乘以矩阵WQ，右边的项量乘以矩阵WK。接着得到q和k这两个项量，将它们进行点乘，再将结果相加，最终得到一个标量，这个标量就是（α）。
• 实际上，还有其他计算（α）的方式，比如右边提到的datap方法。这种方法同样是将两个项量通过WQ和WK得到q和k，然后将它们串联在一起，经过一个激活函数，再通过一个变换，最终得到（α）。总之，有很多不同的方法可以用来计算attention，计算这个阿法的数值，计算关联程度。在接下来的讨论中，我们将使用左边提到的方法，这也是当前最常用的方法，也是在Transformer中使用的方法。
• 接下来，我们将讲解如何计算这个（α），一旦讲完这一部分，我们就可以结束这次课程，或者看看大家是否有任何问题。总之，通过这两个向量，我们可以计算出（α）。

6、self-attention计算α关联性

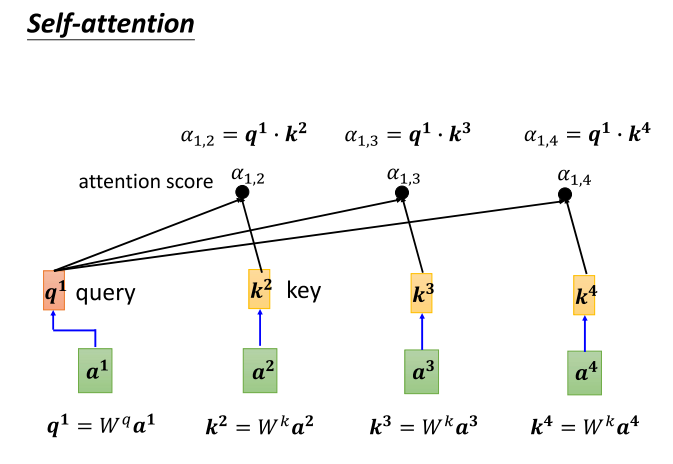
• 在应用于self attention中，你需要将a one与a two、A3以及A4分别计算它们之间的关联性，也就是计算它们之间的阿法。那么具体怎么做呢？你将a one乘以w q，得到q one。这个q有个名字，我们称之为query。它就像是你在搜索引擎中搜寻相关文章时使用的关键字，所以这里叫做query。接下来，a two、A3和A4你都要分别乘以w k，得到k这个向量。而k这个向量有一个名字，叫做key。然后，你将这个query（q one）与key（k two）做内积运算，就得到了阿法。我们用阿法一二来表示，表示query一提供，key二提供时，它们之间的关联性。这个关联性又被称为attention score，即注意力分数。
• 好了，q one与k two（即a one与a two）计算出它们的attention score后，接下来也需要与A3和A4来计算。具体操作是将A3乘以w k，得到K3，得到另外一个key；A4乘以w k，得到K4，也得到另外一个key。然后，将K3这个key与q one这个query做内积运算，得到1与3之间的关联度，得到1与3之间的attention。同样，将K4与q one做内积运算，得到阿法14，得到1与4之间的关联度。这样，a one就计算出了它与a two、A3和A4之间的关联性，而这个关联性用attention score Alpha来表示。

7、self-attention得到α‘

• 在深入讨论中，当我们处于第10章时，q one（也就是自身）也需要与自己计算关联性。因此，你同样需要将a one乘以w k，得到k one，再将q one与k one计算它们之间的关联性。这个自身与自身计算关联性的过程可能会显得有些特殊，但实际上它的重要性不可忽视。你可以在做作业时尝试一下，看看这个步骤对结果的影响有多大。
• 接下来，我们将计算a one与每一个向量的关联性。然后，进行Softmax操作。这里的Softmax与分类时使用的Softmax是一样的。我们将所有的阿法值乘以指数，然后将这些指数值相加并进行标准化，得到Softmax的输出。因此，Softmax的输出是一系列阿法块。或许你会问，为什么这里要使用Softmax？刚才提到分类时使用Softmax有一些道理，只是还没详细解释。而在这里，使用Softmax并没有特别的理论基础，你也可以选择其他的激活函数，例如有人尝试使用一个叫做reader的激活函数，发现在某些情况下比Softmax效果更好。所以，你并非必须使用Softmax，你可以尝试其他激活函数，最终结果取决于实验效果。

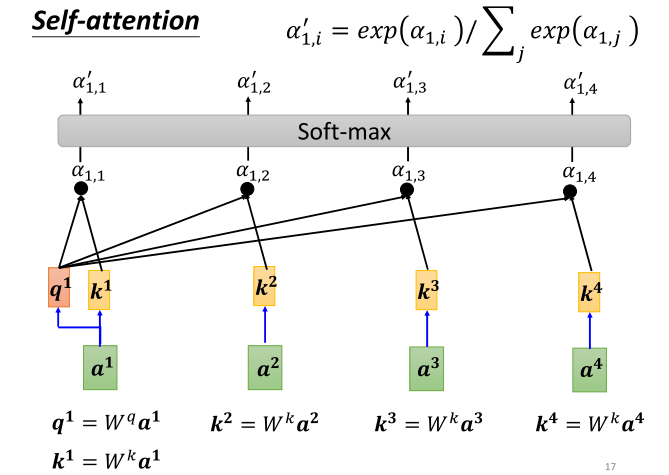
8、self-attention得到新向量b1

• 到了Alpha plan这一步，我们要根据这个Alpha plan抽取出sequence中的重要信息。通过这个Alpha plan，我们已经知道哪些项量与a one有最强的关系。接下来的任务就是基于这种关联性，根据attention的分数来抽取重要的信息。
• 具体而言，我们将对a one到a four中的每个项量乘以WV，得到新的项量，用v one、v two、v three、v four来表示。然后，将这些新的项量乘以attention的分数，即Alpha plan。将它们加起来，用公式表示，即将每个v乘以Alpha plan得到b one。
• 你可以想象，如果某个项量得分越高，比如a one与a two的关联性很强，那么对应的Alpha plan值就很大。在进行权重上的计算时，得到的b one的值就可能更接近b two。因此，具有最大值的那个项量，其attention分数最高，该项量对最终抽取的结果影响较大。

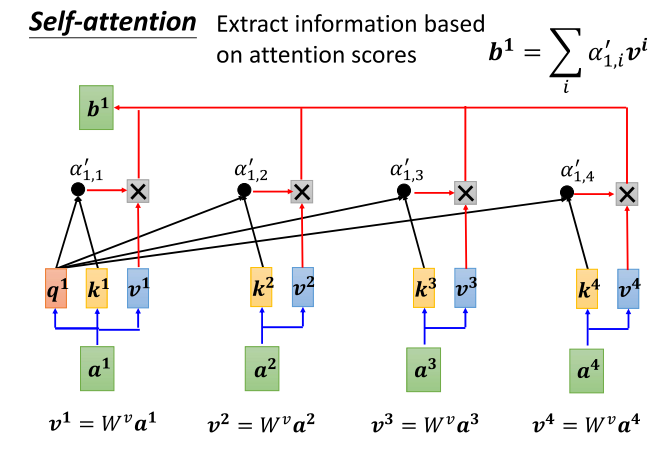
9、self-attention整体得到b1

• 好，关于self-attention，我们上周已经演示了如何根据输入序列得到相应的输出。self-attention的任务是接收一系列输入向量并生成一系列输出向量。我们上周介绍了如何根据输入向量序列得到 b one 的过程。我们停在那里，如果你错过了上周的内容，那正好，我们现在将再次讨论如何从这一系列向量中得到 b two。其实，从这一系列向量得到 b one 和 b two 的操作是一样的。
• 所以，我们再次强调一点：b one 到 b four，并不需要按顺序生成。你不必先计算 b one，然后计算 b two，再计算 b three，最后计算 b four。实际上，它们是同时计算出来的。

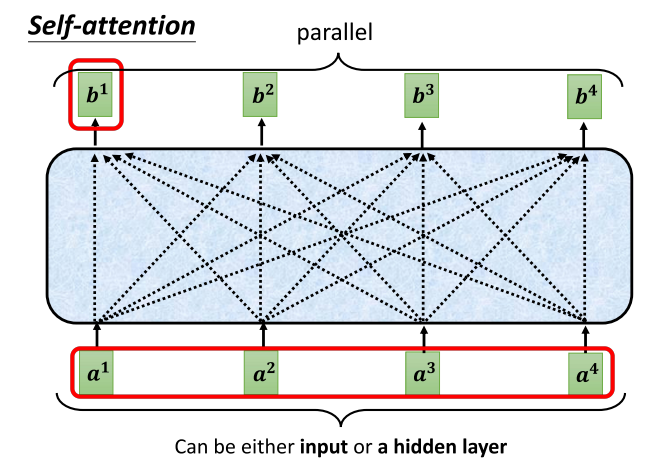
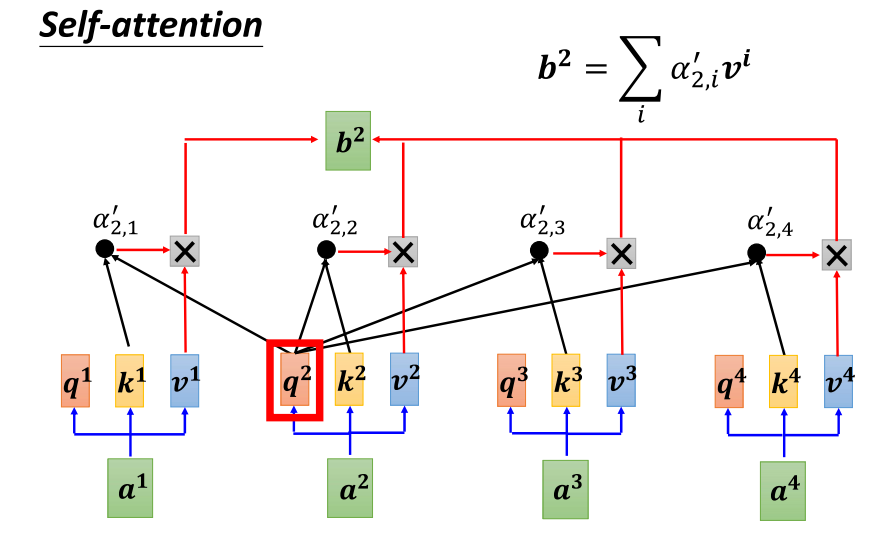
10、self-attention整体得到b2

• 好，现在我们来讨论如何计算 b two。我们的主角是 a two，a two 会通过一个变换（transform）乘上一个矩阵，得到 Q2。接下来，我们将使用 Q2 对 a one 到 a four 这四个位置进行 attention score 的计算。计算 attention score 的方法是将 Q2 分别与 k one、k two、k three、k four 做点积，得到四个分数。然后，可能会进行一些归一化操作，比如使用 Softmax，得到最终的 attention score，我们用 Alpha 21 来表示。
• 得到 attention score 之后，我们将这些分数分别与 v one、v two、v three、v four 相乘，得到 Alpha 21 乘以 v one 得到 b one，Alpha 22 乘以 v two 得到 b two，以此类推，最后将它们全部相加得到 b two。
• 具体而言，我们可以表示为：b two = Alpha 21 * v one + Alpha 22 * v two + Alpha 23 * v three + Alpha 24 * v four。
• 这样，我们就得到了 b two 的计算方式。同理，你可以使用相似的步骤计算出 b three 和 b four，从而了解如何从 a one 到 a four 计算出 b one 到 b four。

11、从矩阵乘法讲述self-attention如何运作：三个重要矩阵：Wq,Wk,Wv

• 好，我们重新从矩阵乘法的角度来理解一下刚才讲的 self attention 运作的过程。我们已经知道对于每个 a（a one 到 a four），它们分别产生了 QKV（q one k one v one 到 q four k four v four）。我们可以用矩阵运算的方式表示这个操作。
• 首先，我们将每个 a 与矩阵 Q 进行乘法，其中 Q 由 WQ 表示，得到 QI（q one 到 q four）。这里的 I 表示一个矩阵，其中的颜色代表了 a one 到 a four。同样，我们将每个 a 与矩阵 K（由 WK 表示）相乘，得到 KI（k one 到 k four）。然后，将每个 a 与矩阵 V（由 WV 表示）相乘，得到 VI（v one 到 v four）。将这些矩阵拼接起来，我们得到了大矩阵 I（大 i），其中包含了输入的所有信息。
• 接下来，我们将大矩阵 I 分别乘上三个矩阵，分别是 WQ、WK、WV，得到了大矩阵 Q、K、V。这里的 Q、K、V 分别包含了 q one 到 q four、k one 到 k four、v one 到 v four。
• 总结一下，对于输入的每个 a，我们通过乘上不同的矩阵得到了对应的 QKV，其中 Q 是通过乘上 WQ，K 是通过乘上 WK，V 是通过乘上 WV 得到的。这样，我们从 a 得到了 QKV 的过程就是将输入的向量序列乘上三个不同的矩阵，得到了 q、k、v。

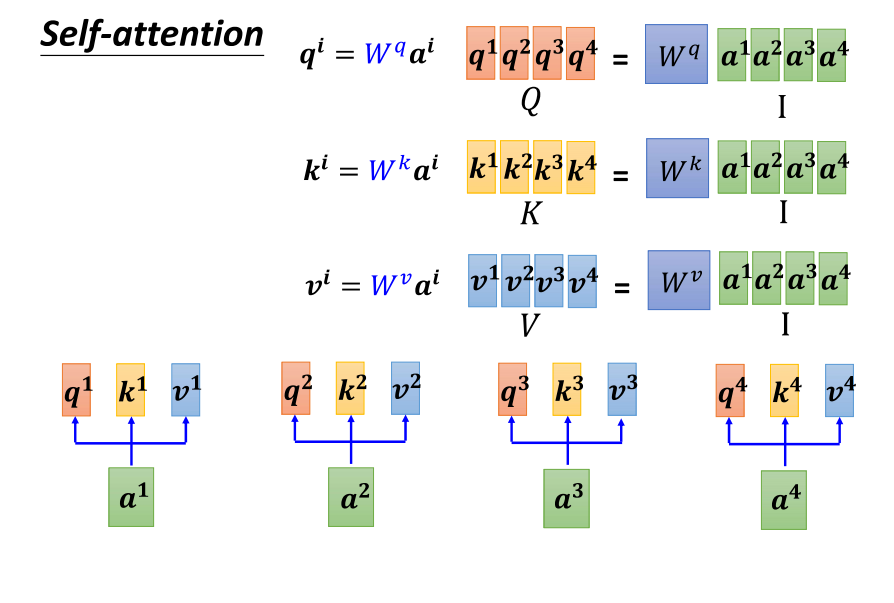
12、从矩阵乘法讲述self-attention计算α

• 下一步我们要做的是计算 attention 分数。从矩阵操作的角度来看，这是如何进行的呢？对于每个 q，它都会与每个 k 做内积操作，得到相应的 attention 分数。从矩阵的角度来看，这实际上是将 q one 与 k one 做内积，得到阿法 one one。将 k one 的背后项量表示成一个较宽的箭头，表示它是全局的。同理，阿法 one two 是 q one 与 k two 做内积得到的，阿法 one three 是 q one 与 K3 做内积得到的，阿法 one four 是 q one 与 K4 做内积得到的。这四个步骤的操作可以看作是将 k one 到 k four 拼接起来，看作是一个矩阵的四个列向量。将这个矩阵乘上 q one，得到另一个项量。这个项量的值即为 attention 分数阿法 one one 到阿法 one four。
• 总结一下，将 q one 乘上由 k 所组成的矩阵，就得到了阿法 one one 到阿法 one four，这表示了 q one 与输入的每个 k 的关联性。

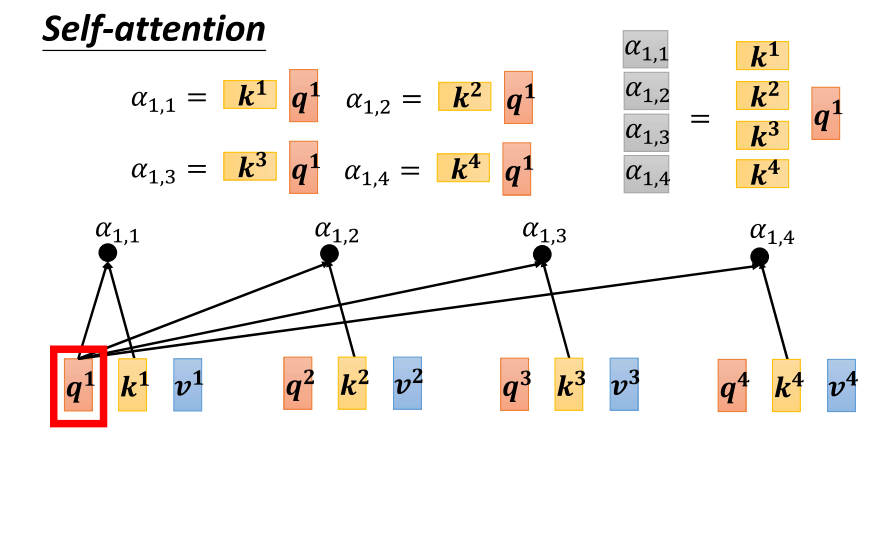
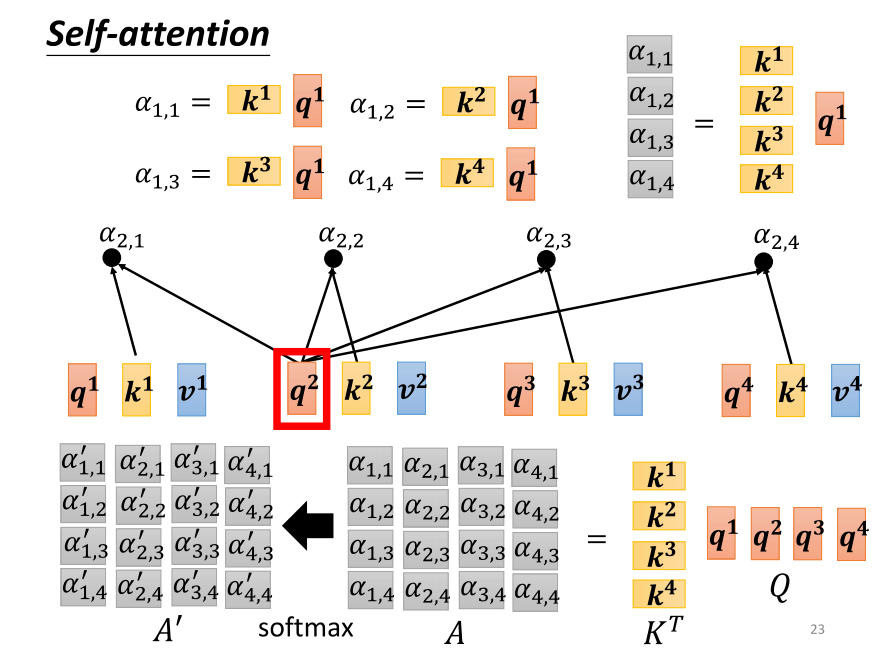
13、从矩阵乘法讲述self-attention并行计算各种α

• 我们之前提到，不仅 q one 需要计算与 k one 到 k four 的 attention 分数，而且 q two 也需要计算与 k one 到 k four 的 attention。为了计算 q two 对 k one 到 k four 的 attention，我们将 q two 乘上 k one 到 k four，得到阿法 two one 到阿法 two four。同样，对于 Q3 和 q four，操作也是类似的。这些 attention 分数的计算可以视为两个矩阵的相乘，其中一个矩阵的列向量是 k one 到 k four，另一个矩阵的列向量是 q one 到 q four。将这两个矩阵相乘，得到的矩阵通过 transpose 操作，最后进行 Softmax 得到归一化的 attention 分数。
• 在这里，我们将 k 的 transpose 乘上 q 得到一个矩阵 a，a 中的值表示了 q 和 k 之间的 attention 分数。我们通常对这些 attention 分数进行 normalization 操作，一种常见的方式是使用 Softmax，对每个 color 进行 Softmax 操作，确保每个 color 中的值相加为一。虽然我们提到了 Softmax，但也要注意，Softmax 并不是唯一的选择，你也可以尝试其他操作，比如 Redo。
• 在这里，我们用 API 表示通过 Softmax 操作后的结果，得到了 normalized 的 attention 分数。接下来，我们已经计算出了这些 attention 分数，下一步是什么呢？

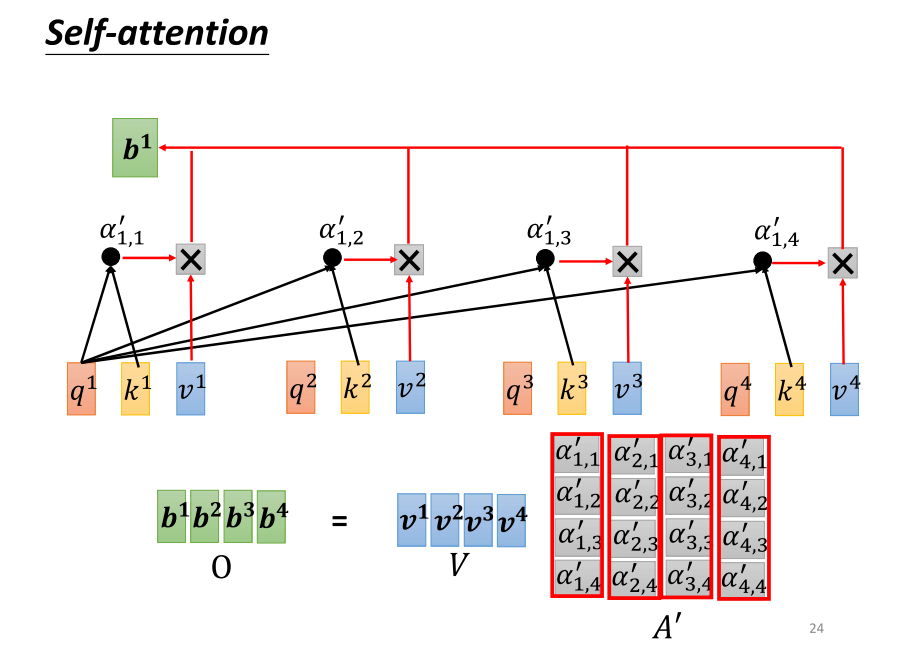
14、从矩阵乘法讲述self-attention得到b1

• 接下来，我们要讨论下一个步骤。在我这个投影片上，发现了一个小小的错误，应该是 “prime” 而不是 “head”。我最早写成了 “head”，但之后改成了 “prime”，这个地方却没有更新过来。
• 好的，现在我们要将 v（v one 到 v four）乘上这边的 Alpha（阿法），然后得到 b。得到了 b 之后，这个 b 是如何计算的呢？我们将 v one 到 v four 拼接在一起，将其看作是一个大的矩阵 V，包含了四个颜色。然后，将 V 乘上 API（经过 Softmax 操作后的 attention 分数）的第一个颜色，得到的结果就是 b one。如果你熟悉线性代数，你会知道将 API 乘上 v，相当于将 API 的第一个颜色乘上 v 矩阵，得到了输出矩阵的第一个颜色。将 a 的第一个颜色乘上 v 矩阵，其实就是将 v 矩阵的每个颜色根据 a 的每个元素进行加权，然后得到 b one。这个操作就是将 b one 乘上权重，将 v two 乘上权重，将 B3 乘上权重，将 B4 乘上权重，全部加起来，就得到了 b one。从矩阵操作的角度看，就是将 API 的第一个颜色乘上 b，得到 b one。
• 然后，接下来就是类似的操作，依此类推。将 API 的第二个颜色乘上 b 得到 b two，将 API 的第三个颜色乘上 b 得到 B3，将 API 的最后一个颜色乘上 b 得到 b four。所以，我们就是将 F 矩阵乘上 b 矩阵，得到 O 矩阵。O 矩阵的每个颜色就是 self attention 的输出，也就是 b one 到 b four。

15、从矩阵乘法讲述self-attention整体

• 在我们讲解操作的过程中，一开始的时候，我们提到了先产生 QKV。接着，根据这个 Q，我们找出相关的位置，并对应到 B 座的位置上。实际上，这一系列操作只是一连串的矩阵乘法而已。让我们再复习一下刚才看到的矩阵乘法：
• 首先，i 是什么？i 是我们的输入，是 self attention 的输入。self attention 的输入是一串 Vector，排列成矩阵的颜色，也就是 i。所以 i 是 self attention 的输入。然后，将这个输入分别乘上三个矩阵 WQ、WK 和 WV，得到大 Q、大 K 和大 V 这三个矩阵。
• 接下来，将大 Q 乘上 K 的转置，得到 A 这个矩阵。A 的矩阵可能会经过一些处理，得到 A’。有时候我们会称 A’ 为 attention 的矩阵。
• 然后，将 A’ 乘上 B，就得到 O。O 就是 self attention 这个层的输出。所以，self attention 的输入是 i，输出是 o。
• 你会发现，在 self attention 层里，虽然进行了复杂的操作，但实际上需要学习的参数只有 WQ、WK 和 WV。只有这三个参数是未知的，需要通过我们的训练数据找到的。其他的操作都是人为设定好的，不需要通过训练数据找到。所以，WQ、WK 和 WV 是需要通过训练数据找到的，而整个操作从 i 到 o 就是进行了 self attention。

四、Multi-head Self-attention

1、多头注意力机制的变形：关注不同的相关性

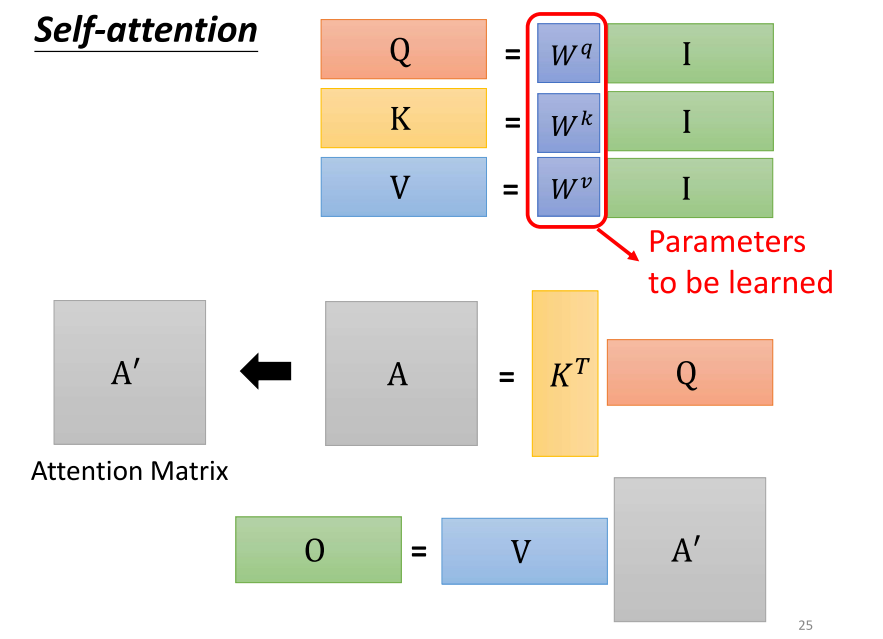
• 在 Self Attention 中，有一个更进一步的版本，称为 Multi-Head Self Attention。这个 Multi-Head Self Attention 在当今的应用中非常广泛。在实际的应用场景中，例如助教办公室里的代码，原始的模型是有 Multi-Head 的，其中 Head 的数量被设定为 2。刚才助教给出了一个提示，建议将 Head 的数量减少一些，改成 1，这实际上可以过一些基本的测试，但并不代表所有任务都适合使用较少的 Head。对于一些任务，比如翻译和语音辨识，使用较多的 Head 可能会获得更好的结果。至于使用多少个 Head，这是另一个超参数，需要进行调整。
• 为什么我们需要较多的 Head 呢？可以想象一下，相关性有很多不同的形式，有很多不同的定义。因此，我们可能不能只有一个 Q，而是应该有多个 Q，每个 Q 负责不同种类的相关性。所以，假设你要做 Multi-Head Self Attention，你可能会这样操作：首先，将输入 A 乘上一个矩阵得到 Q，接下来将 Q 乘上另外两个矩阵，分别得到 Q1 和 Q2。这里的 1 和 2 代表这个位置的几个 Q。因此，这里有 QI1 和 QI2，代表我们有两个 Head。对于同样的位置，再做同样的操作，得到 QJ1 和 QJ2。因此，我们认为在这个问题中有两种不同的相关性，因此我们需要生成两种不同的 Head 来找到两种不同的相关性。
• 既然 Q 有两个，那么 K 和 V 也就需要有两个。接下来，就是如何从 Q 得到 Q1 和 Q2，从 K 得到 K1 和 K2，从 V 得到 V1 和 V2。实际上，就是将 Q、K 和 V 分别乘上两个矩阵，得到不同的 Head。
• 然后，就是在做 Self Attention 的时候，我们按照每一类的 Head 一起做，即 1 这一类的一起做，2 这一类的一起做。例如，QI1 在计算 Attention Score 的时候，就只关注 KI1，不关注 KI2。同样，VI1 在计算加权和的时候，也只关注 VJ1，不关注 VJ2。最终，将得到的结果 BI1 和 BI2 合并，通过一个变换（即再乘上三个矩阵），得到 BI，然后送到下一层。
• 因此，整个操作就是 Multi-Head Attention，是 Self Attention 的一种变形。

五、引入位置信息资讯

1、引入位置信息资讯

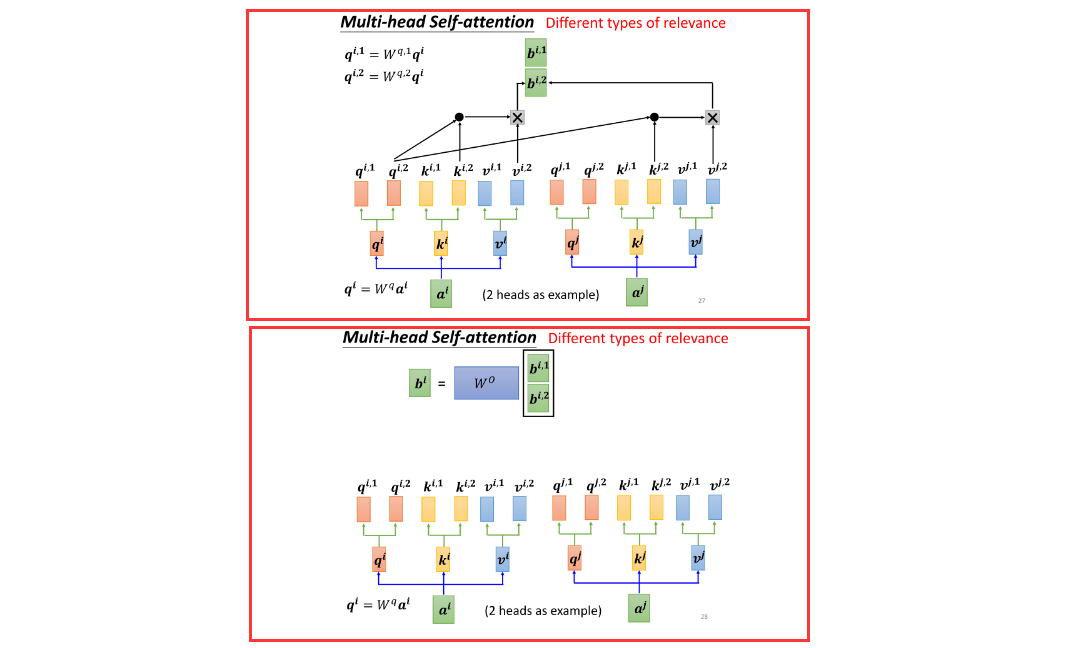
• 到目前为止，我们可以发现 Self Attention 这个层缺少一个可能很重要的信息。这个信息是什么呢？这个信息是未知的信息。想象一下对于一个 Self Attention 层来说，每个输入是出现在序列的最前面还是最后面，它是完全不知情的。你可能会说，刚才不是说有位置 1、2、3、4 吗？但是，这些位置 1、2、3、4 只是我们在投影片上为了帮助大家理解而标记的编号。对于 Self Attention 来说，位置 1 和位置 2、位置 3 和位置 4 之间没有任何差别，这四个位置的操作是一模一样的。对于 Self Attention 来说，位置之间的距离都是相同的，没有任何一个位置距离比较远或者比较近，也没有哪个位置在整个序列的最前面或者最后面。
• 然而，这样的设计可能存在一些问题，因为有时候未知的信息可能很重要。例如，在进行 POS tagging（词性标记）时，你可能知道动词比较不容易出现在句首，所以如果我们知道某一个词汇是在句首的，那么它是动词的可能性可能就比较低。未知的信息往往也是有用的。但是在我们目前为止讲的 Self Attention 操作中，它根本没有未知的信息。那么，我们在做 Self Attention 时，如果认为未知的信息很重要，可以通过使用一种叫做 Positional Encoding 的技术来将未知的信息引入。
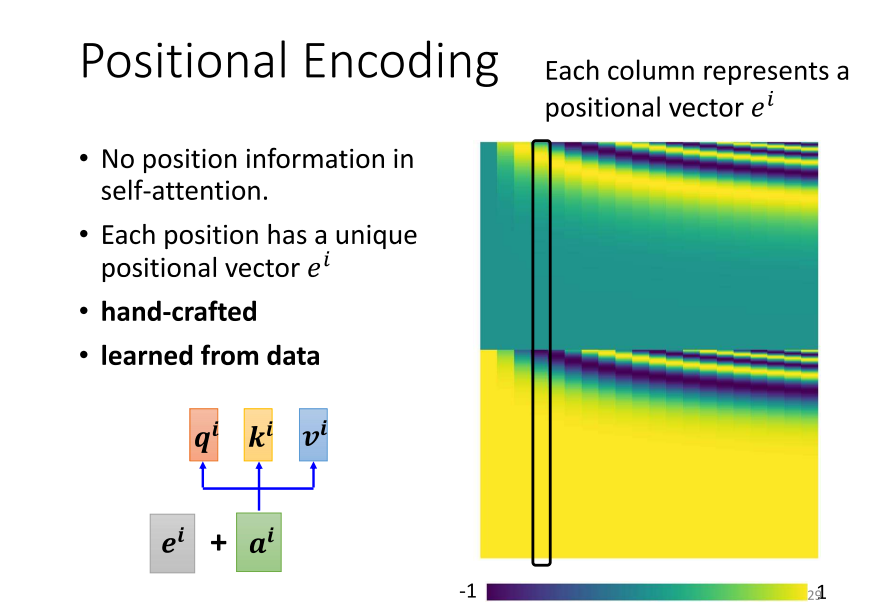
• Positional Encoding 的实现方法是为每一个位置设定一个 Vector，称为 Positional Vector。这里用 E 表示，上标 i 代表位置。每个不同的位置都有一个不同的 Vector，比如 E1、E2、E3 等。然后，将这个 E 加到输入 A 上，就完成了。这样，我们就告诉了 Self Attention 每个位置的信息。如果它看到输入 A 似乎被加上了 E，那么它就知道现在出现的位置是在 i 这个位置。
• 那么，Positional Vector（位置编码）长什么样呢？最早的 Transformer 论文中，它的 Positional Vector 是这样的：每个位置对应一个不同的 Vector，第一个位置是 E1，第二个位置是 E2，以此类推。这样，它就将这个 Vector 放在第一个位置，将这个 Vector 加到第二个位置上，将这个 Vector 加到第三个位置上，以此类推。每个位置都有一个专属的 Vector。
• 需要注意的是，这样的 Positional Vector 是手动设定的，是人工设计的。人工设计的因素存在一些问题，例如如果我现在定这个因素的时候只定到 1 到 128，而现在长度 c 是 129，怎么办呢？这可能会导致一些问题。当然，在最早的 Transformer 论文中，这个 Vector 是通过一些规则产生的，通过一种神奇的方式，通过一些心理学上的方式产生的。但是，当然你可能会有新的问题，为什么要使用 sin 和 cosine 呢？为什么不是其他的东西？为什么一定要这样手动设计 Positional Vector 呢？实际上，你不一定要这样产生 Positional Encoding，Positional Encoding 仍然是一个正在研究的问题。你可以创造自己的方法，甚至 Positional Encoding 是可以根据数据学出来的。

2、Positional Encoding技术

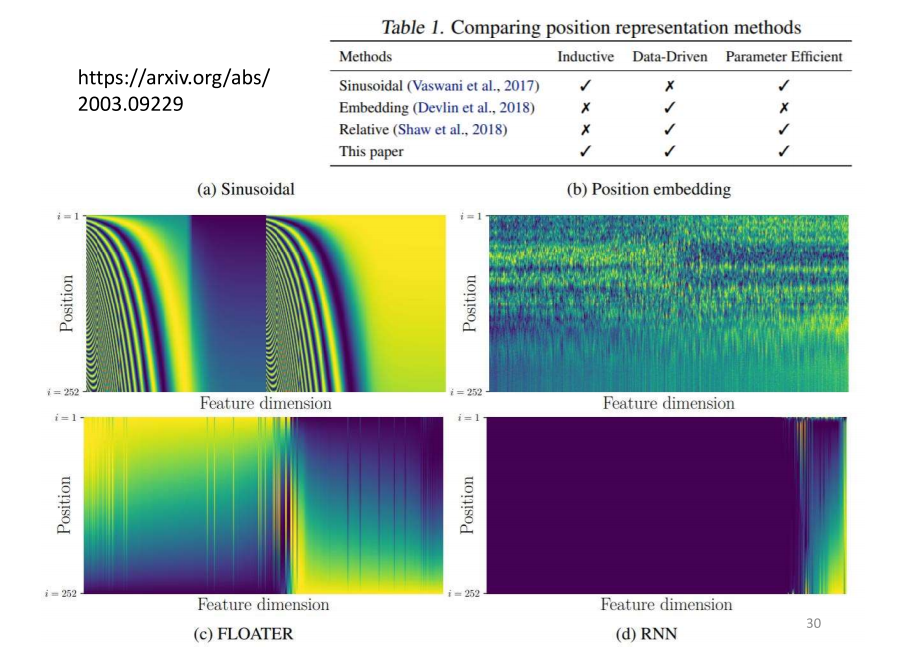
• 在处理 Positional Encoding 方面，你可以再参考一下相关文献，因为这是一个当前正在研究的问题。举例来说，我引用了一篇去年发布在 ARCHIVE 上的论文，这显示这些都是较新的研究。在文献中，对于 Positional Encoding 进行了比较，并提出了一些新的方法。最早的 Positional Encoding 使用了一种神奇的单一方式生成，而如果你将 Positional Encoding 中的数值视为网络参数的一部分并直接进行训练，效果可能如图所示。
• 这张图是横着看的，每一行代表一个位置。最初的 Positional Encoding 使用的是一种赛方程生成的方法，而另一种是通过神经网络（RNN）生成的。另外，有一篇论文提出了一种名为 “floater” 的方法，通过一种神奇的叙述方式产生 Positional Encoding。总之，有许多不同的方法来生成 Positional Encoding，包括神经网络生成、赛方程等。目前我们尚不清楚哪种方法最为优越，这是当前研究中的一个问题。因此，你无需过于纠结为什么选择 sin 和 cosine，而是应该鼓励提出新的方法。

六、self-attention其它应用

1、其它应用

• 这个 self-attention 在计算机领域中得到了广泛的应用，特别是在 Transformer 模型中。我们之前已经多次提到了 Transformer 模型，这个模型在自然语言处理（NLP）领域非常有名。在 NLP 中，Transformer 被广泛应用于各种任务，如语言翻译、文本生成等，而其中的 self-attention 是这一模型的核心组成部分。
• 然而，需要注意的是，self-attention 并不仅限于在 NLP 相关的应用中使用，它还可以在许多其他问题上发挥作用。在计算机科学和人工智能的其他领域，人们也发现了 self-attention 的潜力，并将其应用于图像处理、语音识别等不同类型的任务。这说明了 self-attention 不仅仅是 NLP 的专属工具，它具有更广泛的适用性，可以为各种领域的问题提供有效的解决方案。

2、Self-attention for Speech

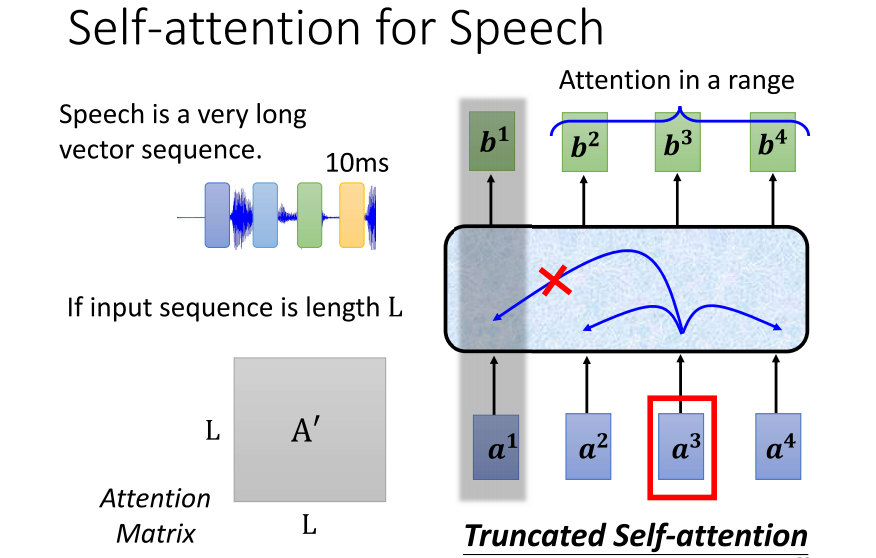
• 在语音处理中，也可以使用 self-attention。然而，在语音处理中使用 self-attention 时，可能需要对其进行一些微小的修改。举例来说，因为语音信号通常表示为一系列向量，每个向量仅代表10毫秒的长度，因此一段语音信号可能包含数千个向量。这使得描述语音信号的向量序列长度非常可观。
• 对于处理具有可观长度的序列，尤其是在计算 self-attention 矩阵时，其复杂度与序列长度的平方成正比。计算 attention matrix a pi 需要进行 l 乘以 l 次的运算，如果 l 很大，计算量将变得非常庞大。此外，较大的序列长度还需要更大的内存来存储这个矩阵，这可能使训练变得困难。
• 为了应对这个问题，引入了一种叫做 self-attention 的技术。在使用 self-attention 时，不需要考虑整个句子，而是只需关注一个较小的范围。具体范围的选择是人为设定的，通常取决于对问题的理解。在语音辨识中，可能只需关注一个小范围内的信息，即使不考虑整个句子，也足以判断特定位置的上下文信息。这样的做法可以加快运算速度，降低计算复杂度。

3、Self-attention for lmage

• 影像处理中同样可以应用 self-attention 技术。在探讨如何将 self-attention 应用在影像上时，我们需要重新审视 self-attention 的适用范围。在之前的讨论中，我们强调了 self-attention 在输入为一系列项量或是一个向量集时的适用性。
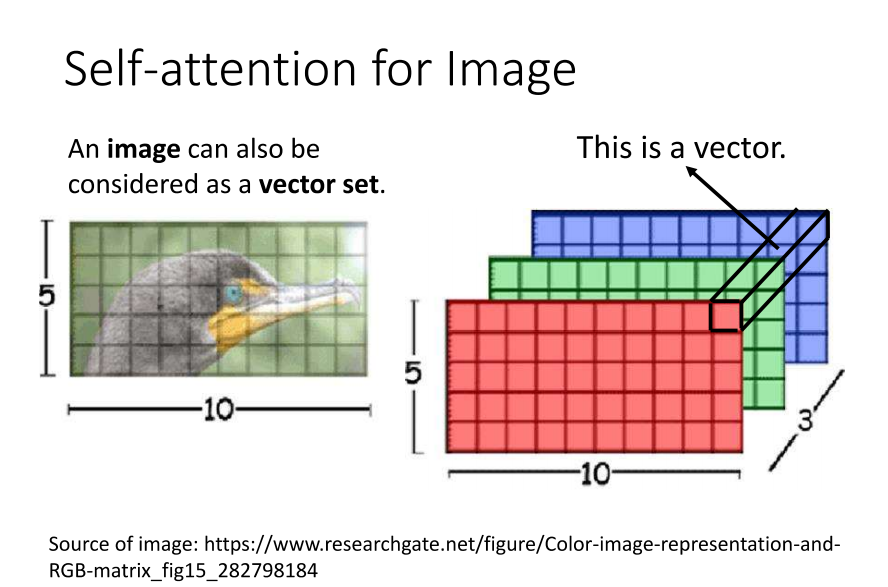
• 回顾我们之前在讨论卷积神经网络（CNN）时提到的观点，影像可以被看作是一个很长的向量。然而，我们也可以采取另一种观点，将一张图片视为一个向量的集合。这样做的方法是将一张图片表示为一个张量，其大小为 5x10x3，代表 RGB 三个通道。在这个张量中，每个位置的像素可以被看作是一个三维的项量。因此，整张图片实际上是由 5x10 个三维项量构成的。
• 从这个角度来看，影像本质上也是一个向量的集合。既然它也是一个向量的集合，那么我们完全可以使用 self-attention 来处理一张图片。那么，是否有人已经尝试使用 self-attention 处理图片呢？

4、Self-attention for lmage例子

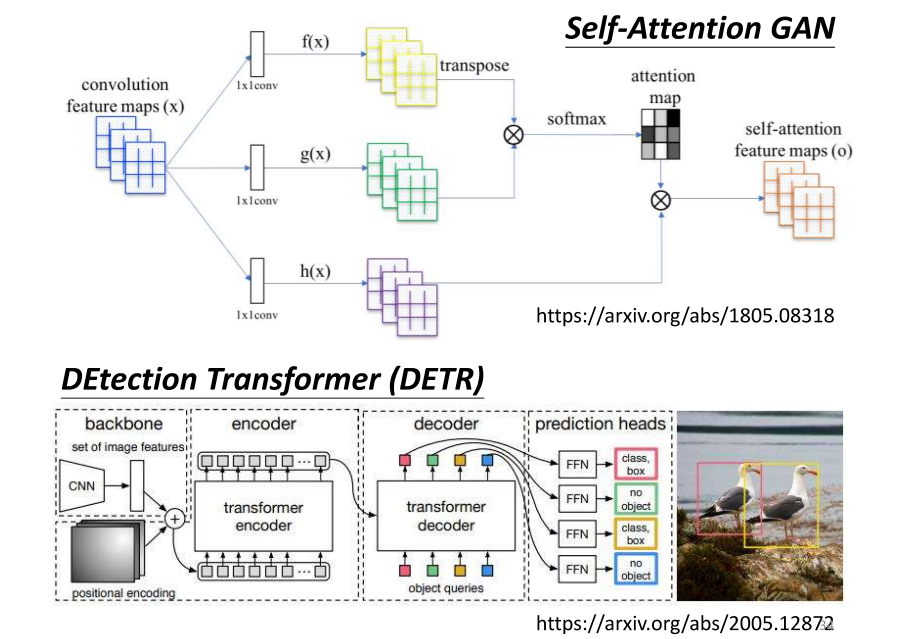
• 是有的;那这边就举了两个例子来给大家参考;那先把silver Tension用在影像处理上;也不算是一个呃非常石破天惊的事情;好那我们可以

5、Self-attention v.s.CNN

• 来比较一下 self-attention 和 CNN 之间存在的差异或关联。如果我们今天使用 self-attention 处理一张图片，这意味着你要考虑每个像素点，其中每个像素点会生成一个查询（query），其他像素点会生成一个键（key）。在进行这种交互的时候，你在思考的不再是一小部分信息，而是整张影像的信息。
• 然而，回顾我们上周讨论的 CNN，CNN 可以被视为 self-attention 的一种简化版本。在进行 CNN 时，我们只考虑 receptive field（感受野）内的信息。相比之下，在进行 self-attention 时，我们考虑整张图片的信息。因此，CNN 可以被看作是 self-attention 的简化版本，或者你可以反过来说，self-attention 是一个对 CNN 进行了复杂化的方法。
• 在 CNN 中，我们需要确定 receptive field 的大小，每个神经元只考虑 receptive field 内的信息。而 receptive field 的大小是由人工决定的。我们上周也花了些时间讨论 receptive field 有哪些可能的设计。
• 而对于 self-attention，我们使用 attention 机制来找出相关的像素点，就好像 receptive field 是自动学出来的一样。模型会自行决定 receptive field 的形状以及以哪个像素为中心，哪些像素是需要考虑的，哪些是相关的。因此，receptive field 的范围不再由人工划定，而是由机器自动学习得出。这里讨论了 self-attention 与 CNN 之间的关系。

6、Self-attention v.s.CNN

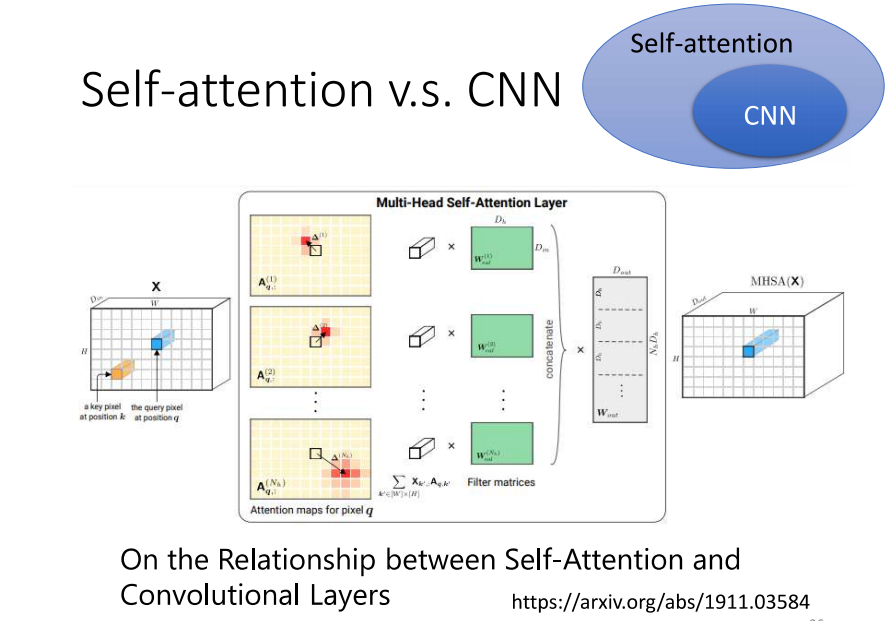
• 在这篇论文中，会使用数学的方式严谨地告诉你，其实这个 CNN 就是 self-attention 的特例。只要设定合适的参数，self-attention 就可以完成与 CNN 一模一样的任务。因此，CNN 的函数集合（function set）长这个样子，而 self-attention 的函数集合长这个样子。所以，self-attention 是一个更加灵活（flexible）的 CNN，而 CNN 则可以看作是有一定限制的 self-attention。只要通过一些设计和限制，self-attention 就会变成 CNN。
• 这不是很久以前的论文，它在网络上发布的时间是 2019 年 11 月。因此，我们今天上课讲的内容都是相当新颖的信息。既然 CNN 是 self-attention 的一个子集，而 self-attention 更为灵活，那么在讲到过拟合时，我们提到了比较灵活的模型需要更多的数据。如果数据不足，就有可能发生过拟合。相反，小型的模型，或者说具有一定限制的模型，在数据较少时可能不容易过拟合。如果这些限制设置得当，也可以获得不错的结果。

7、Self-attention v.s.CNN

• 今天我们通过使用不同量级的数据来训练 CNN 和 self-attention，确实可以观察到我之前提到的现象。这个实验结果来自于 Google 的一篇名为 “An Image is Worth 1616 Words" 的论文。在该论文中，它将 self-attention 应用于图像，将一张影像拆分成 16x16 个小块，将每个小块想象成一个 word。因为通常 self-attention 更常用于自然语言处理，所以将图像的每个小块视为一个 word，并取了一个有趣的标题，叫做 "An Image is Worth 1616 Words”。
• 横轴表示训练的影像数量，纵轴为实验结果。从实验结果中可以发现，对于 Google 来说，当使用的数据量较小时，即 1000 万张图的情况下，self-attention 的表现较差，而 CNN 的表现较好。而在数据量较大的情况下，即 3 亿张图片的情况下，self-attention 的表现逐渐超过 CNN，表现更好。这说明随着数据量的增加，self-attention 的性能逐渐提升。然而，当数据量较小时，CNN 的性能优于 self-attention。
• 为什么会出现这样的现象呢？我们可以从 CNN 和 self-attention 的灵活性来解释。Self-attention 具有较大的灵活性，因此需要更多的训练数据，否则容易发生过拟合。而 CNN 的灵活性较小，在训练数据较少时，可以获得较好的结果。但是在训练数据较多时，它无法从更大量的训练数据中受益，因此性能相对较差。这就是 self-attention 和 CNN 的比较结果。你可能会问，在 self-attention 和 CNN 中，哪个更好呢？实际上，你可以根据具体情况选择使用。在作业4中，如果你需要一个强基线，我给你一个提示，可以使用 Conformer 模型，该模型既包含了 self-attention，也使用了 CNN。

8、Self-attention v.s.RNN

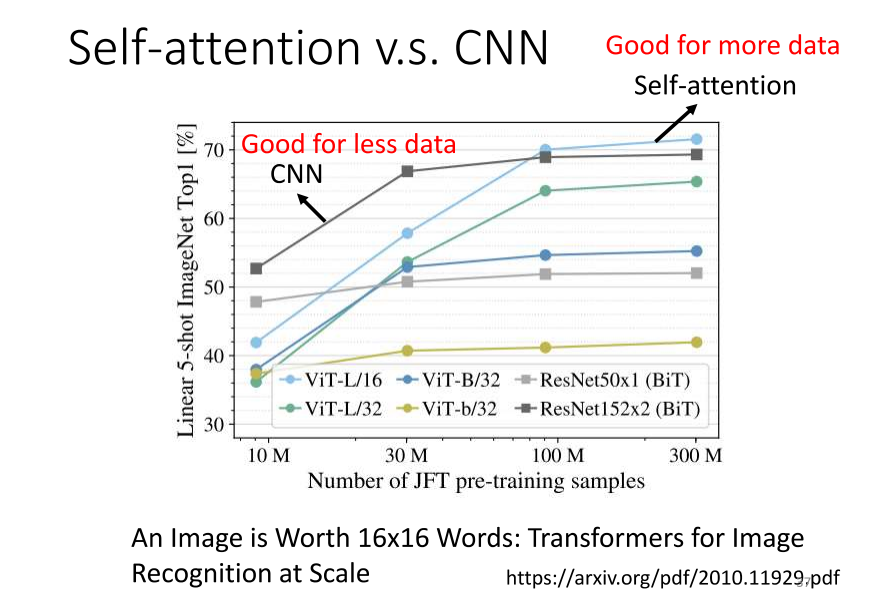
• 好，我们现在将 self-attention 与 RNN 进行比较。RNN，即循环神经网络，其实在这门课里我们不会详细讲解，因为循环神经网络的很大一部分功能可以用 self-attention 来替代。在这门课里，我们不会特别拿出 RNN 来讲解，但是如果你对 RNN 感兴趣的话，我可以简要介绍一下。
• RNN 和 self-attention 都是用于处理输入是序列的情况。在 RNN 中，你的输入序列是一系列的向量，然后你有一个 RNN 的 block，在这个 block 里，它会读入一个 memory 的向量和第一个输入向量，然后输出一个结果。根据这个输出，通常我们称之为隐藏层，然后通过一个全连接网络进行进一步的预测。RNN 这个模块接下来，当第二个序列中的第二个向量作为输入进入时，会将这个向量和前一个时间点产生的输出一起送入 RNN，再生成新的向量，然后传递给全连接网络，进行我们想要的预测。当第三个向量进入时，将第三个向量和前一个时间点产生的输出一起送入 RNN，再生成新的输出，以此类推。
• self-attention 模块与此非常相似，因为它也处理输入是一个向量序列的情况。self-attention 有一组向量，这组向量中的每一个都考虑了整个输入序列，然后将它们送入全连接网络进行处理。同样，self-attention 输出一组向量，然后通过全连接网络进行进一步的处理。如果我们比较 RNN 和 self-attention 的话，它们的输入都是一个向量序列，都经过一些处理后得到新的输出。然而，有一个明显的区别，self-attention 中的每个向量都考虑了整个输入序列，而 RNN 中每个向量只考虑了已输入的向量，没有考虑右边的向量。虽然 RNN 可以是双向的，但它仍然需要将最左边的输入存在 memory 中，然后一路传递到最右边才能被考虑。而 self-attention 没有这个问题，它只需要输出一个查询和一个键，只要它们匹配起来，就可以从整个序列中轻松地提取信息。
• 还有一个重要的不同点是，在处理输入序列和输出序列时，RNN 是不能够进行并行处理的，它必须一个一个地生成。而 self-attention 具有并行处理的优势，可以同时生成输出序列中的所有向量。这使得 self-attention 在计算速度上更为高效。因此，很多应用逐渐将 RNN 的架构改成 self-attention 的架构。
• 如果你想深入了解 RNN 和 self-attention 的关系，你可以查阅 “Transformers are RNNs” 这篇文章，它会告诉你，加上一些东西后，self-attention 其实变成了 RNN。这篇文章是去年 6 月放在 arXiv 上的，所以我们今天讲的都是一些非常新的研究成果。至于 RNN 的部分，我们这门课不会涉及，但如果你对 RNN 有兴趣，可以在这门课之前的录音中找到相关内容。

9、Self-attention for Graph

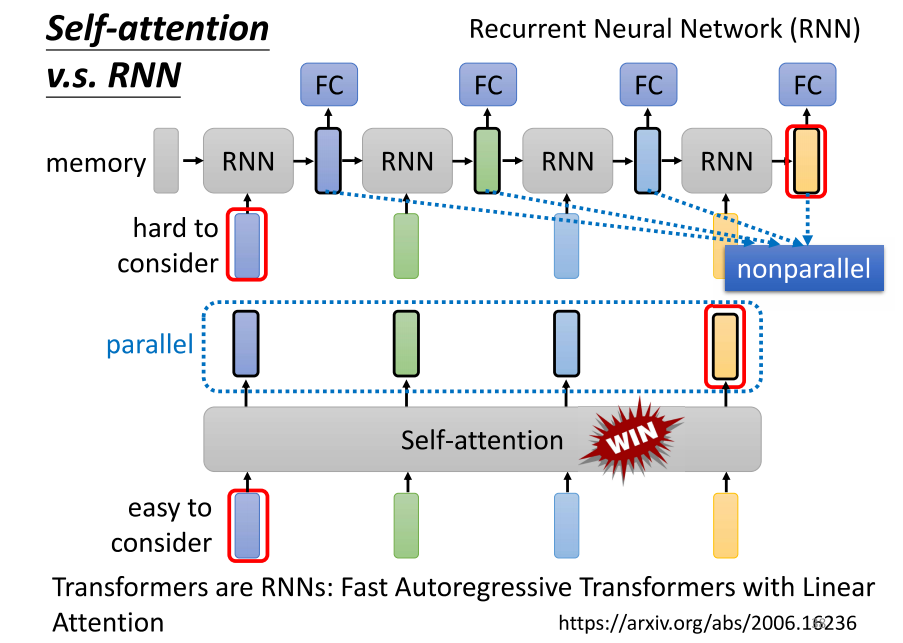
• 最后呢，self attention也可以被用在图(Graph)上面。回忆一下，在这门课一开始的时候，我们提到过图也可以看作是一堆向量。如果是一堆向量，就可以使用self attention来处理。然而，当我们把self attention应用在图上时，有一些特殊之处。
• 在图上，我们不仅仅有每一个节点(Node)，每一个节点可以被表示成一个向量，还有边的信息。我们知道哪些节点之间是有连接的，即哪些节点是有关联的。我们知道哪些向量之间是有关联的。在之前使用self attention时，关联性是由模型自动找出的。但是现在，有了图的信息和边的信息，关联性也许就不需要通过机器自动找出来了。这个图上的"h"已经暗示了节点之间的关联性。因此，当你把self attention应用在图上时，你可以选择在进行attention匹配计算时，只计算与"h"相连的节点。在这个图中，例如，节点1和节点8是相连的，那么我们只需要计算节点1和节点8之间的注意力分数。节点6相连，所以只有节点6需要计算attention的分数。节点1和节点5相连，所以只有节点1和节点5需要计算attention的分数，以此类推。
• 如果两个节点之间没有相连，那么很有可能意味着这两个节点之间没有关系。既然没有关系，我们就不需要再去计算它们的attention score，直接将它设为0就好了。因为这个图通常是人为根据某些领域知识构建的，而领域知识已经告诉我们这两个向量彼此之间没有关联。我们就没有必要再用机器去学习这个事情。
• 实际上，当我们把self attention按照我们讲的这种限制应用在图上时，其实就是一种图神经网络(Graph Neural Network)，也就是一种GNN。我知道GNN现在也是一个很炫酷的主题。不过，我不能说self attention涵盖了所有GNN的各种变体，但把self attention用在图上是GNN中的一种类型。
• 在这里，我们无法深入讨论GNN，这个领域的知识也是相当深奥的。你可以参考助教之前上课的链接，他花了近3个小时来讲解图神经网络，但实际上还没有讲完。图神经网络的知识也是相当深刻的，我们今天的课程无法涵盖这个范围。

10、To learn More…

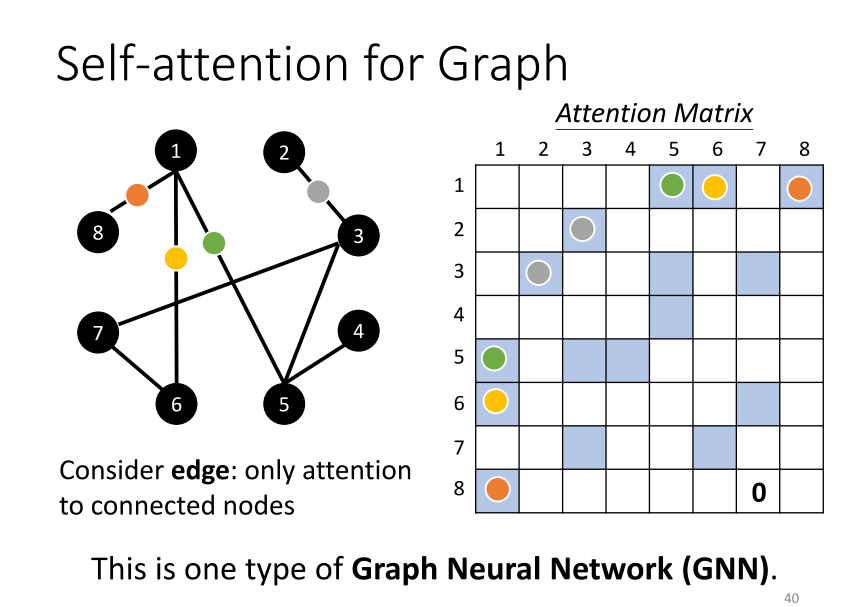
• 那实际上，这个self attention，它有非常非常多的变体。你可以查阅一篇论文，叫做"Long Range Arena"，里面详细比较了各种不同的self attention的变体。因为self attention最大的问题在于，它的运算量非常庞大。所以，如何减少self attention的运算量是一个未来的研究重点。
• 你可以看到，这里有各种各样的self attention的变体。self attention最早是应用在Transformer模型上，因此很多时候，当人们提到Transformer时，实际上指的就是self attention。有人认为广义的Transformer就是指self attention。后来，各种各样的self attention的变体都以“former”结尾，比如informer、performer、Reformer等等。所以，现在各种self attention的变体通常被称为叉叉former。
• 你可以看到图上往右表示运算的速度。因此，有很多新的叉叉former，它们的速度可能比原来的Transformer更快。但是，速度提升通常伴随着性能下降。这个图上的纵轴表示性能，所以这些新的叉叉former往往在性能上稍逊于原来的Transformer，但速度更快。
• 那到底什么样的self attention才能够既快又好，这仍然是一个尚待研究的问题。如果你对self attention有进一步的研究兴趣，可以查看一下"Efficient Transformer"这篇论文，里面会直接介绍各种self attention的变体。当然，这个内容可能超出了我们当前课程的范围，我们就在这里停一下。

No.2 Transformer

等有空再继续看李宏毅老师的B站课程！