题目难度: 中等
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
实现一个二叉搜索树迭代器类 BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
- BSTIterator(TreeNode root) 初始化 BSTIterator 类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。
- boolean hasNext() 如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。
- int next()将指针向右移动,然后返回指针处的数字。
- 注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:
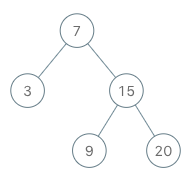
- 输入
- inputs = [“BSTIterator”, “next”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”, “next”, “hasNext”]
- inputs = [[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
- 输出
- [null, 3, 7, true, 9, true, 15, true, 20, false]
- 解释
- BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
- bSTIterator.next(); // 返回 3
- bSTIterator.next(); // 返回 7
- bSTIterator.hasNext(); // 返回 True
- bSTIterator.next(); // 返回 9
- bSTIterator.hasNext(); // 返回 True
- bSTIterator.next(); // 返回 15
- bSTIterator.hasNext(); // 返回 True
- bSTIterator.next(); // 返回 20
- bSTIterator.hasNext(); // 返回 False
提示:
- 树中节点的数目在范围 [1, 10^5] 内
- 0 <= Node.val <= 10^6
- 最多调用 10^5 次 hasNext 和 next 操作
进阶:
- 你可以设计一个满足下述条件的解决方案吗?next() 和 hasNext() 操作均摊时间复杂度为 O(1) ,并使用 O(h) 内存。其中 h 是树的高度。
题目思考
- 如何利用二叉搜索树的性质?
- 如何尽可能优化 next() 和 hasNext() 操作的时间复杂度?
解决方案
思路
- 分析题目, 一个很容易想到的思路就是中序遍历, 将二叉搜索树转换成一个有序列表, 存储递增的值
- 然后维护一个当前下标, 每次 next() 操作返回对应的值, 并把下标右移一位即可
- 不过这样虽说 next() 和 hasNext() 操作的时间复杂度都是 O(1), 不过需要额外使用 O(N)的内存, 不满足进阶要求, 如何优化呢?
- 如果我们可以直接对原树进行改造, 将其转换成一颗递增顺序树 (根节点最小, 每个节点的右子节点指向大于它的最小节点), 并维护下个节点 nex, 这样每次 next()操作只需要返回 nex 的值, 并将 nex 设为其右子节点即可
- 这个改造过程正是前面刚做过的题目Leetcode 剑指 Offer II 052. 递增顺序搜索树, 为了方便起见, 我把对应的思路也贴在这里了:
- 回顾二叉搜索树的性质, 其中序遍历的节点本身就是有序的, 所以如果我们保存了前一个节点, 那么在遍历当前节点时, 只需要将前一个节点的右子节点指向它即可, 然后将前一节点更新为当前节点, 以此类推, 这样最终中序遍历完成时, 就得到了题目要求的递增顺序搜索树
- 当然, 我们在遍历到当前节点时, 也需要将其左子节点置为空, 这里之所以将当前节点而不是前一节点的左子节点置为空, 是因为这样才能保证最终所有节点的左子节点都是空, 否则最后一个节点的左子节点就可能不是空, 会导致出现循环
- 利用上述做法, 我们就无需引入额外的列表存储, 也不需要再次遍历了
- 另外在遍历第一个节点时, 由于它没有前一节点, 所以我们可以额外引入一个哨兵节点, 并将最开始的前一节点初始化为哨兵, 这样哨兵的右子节点就是最终形成的树的根, 返回它即可
- 这样我们就只需要在初始化时, 使用 O(h)的空间来改造树, 之后的 next() 和 hasNext() 操作都只需要 O(1)的时间复杂度
- 下面代码中有详细的注释, 方便大家理解
复杂度
- 时间复杂度 O(N)/O(1): 初始化时只需要遍历每个节点一次, 为 O(N); next() 和 hasNext() 操作只需要常数时间, 为 O(1)
- 空间复杂度 O(H): 初始化改造树时的递归调用最多使用 O(H) 栈空间, H 是树的高度
代码
class BSTIterator:
def __init__(self, root: TreeNode):
dummy = TreeNode(0)
pre = dummy
def inorder(node):
# 中序遍历
nonlocal pre
if not node:
return
inorder(node.left)
# 将当前节点的左子节点置为空, 注意不能将pre的左子节点置为空, 否则会漏掉最后一个节点
node.left = None
# 将前一节点的右子节点指向当前节点
pre.right = node
# 更新前一节点为当前节点
pre = node
inorder(node.right)
inorder(root)
self.nex = dummy.right
def next(self) -> int:
res = self.nex.val
# 移动self.nex到中序遍历的下一个节点
self.nex = self.nex.right
return res
def hasNext(self) -> bool:
return self.nex != None
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊