机器人导航地图——Obstacle层的障碍物-Bresenham算法详细解释

文章目录

前言
一、Bresenham算法源码解析
- 1. 函数raytraceFreespace
- 2. 函数inline void raytraceLine
- 3. 函数bresenham2D
二、Bresenham算法——C++代码实现
总结

前言

作者在读源代码时，遇到了下述的代码void ObstacleLayer::raytraceFreespace，不是很好理解，有很多疑惑，于是打算对此部分进行详解，并记下笔记。

void ObstacleLayer::raytraceFreespace(const Observation& clearing_observation, double* min_x, double* min_y,
                                              double* max_x, double* max_y)
{
  clearing_observation的origin_是传感器坐标，传入
  double ox = clearing_observation.origin_.x;
  double oy = clearing_observation.origin_.y;
  pcl::PointCloud < pcl::PointXYZ > cloud = *(clearing_observation.cloud_);

  //得到传感器原点在地图上的坐标
  // get the map coordinates of the origin of the sensor
  unsigned int x0, y0;
  if (!worldToMap(ox, oy, x0, y0))
  {
    ROS_WARN_THROTTLE(
        1.0, "The origin for the sensor at (%.2f, %.2f) is out of map bounds. So, the costmap cannot raytrace for it.",
        ox, oy);
    return;
  }

  // we can pre-compute the enpoints of the map outside of the inner loop... we'll need these later
   //我们可以在内环之外预先计算地图的点。。。我们稍后需要这些
  double origin_x = origin_x_, origin_y = origin_y_;
  double map_end_x = origin_x + size_x_ * resolution_;
  double map_end_y = origin_y + size_y_ * resolution_;


  touch(ox, oy, min_x, min_y, max_x, max_y);


  //接下来的几个判断结构实际上做的主要工作就是不断迭代传感器原点和点云中的点的连线，
  //并对其调用raytraceLine函数，将连线上的点在本层地图上全部标记为FREE_SPACE。
  //这里获取连线时，要注意该点是否超出地图范围，如果超出，则通过相似三角形去除连线在地图外的部分。

  // for each point in the cloud, we want to trace a line from the origin and clear obstacles along it
  //对于点云中的每个点，我们要追踪原点和clear obstacles之间的一条线
  for (unsigned int i = 0; i < cloud.points.size(); ++i)
  {
    //wx wy是当前点云中的点的坐标
    double wx = cloud.points[i].x;
    double wy = cloud.points[i].y;

    // now we also need to make sure that the enpoint we're raytracing
    // to isn't off the costmap and scale if necessary
    //a、b是该点跟传感器原点的距离
    double a = wx - ox;
    double b = wy - oy;

    // the minimum value to raytrace from is the origin
    //如果当前点x方向比地图原点还小
    if (wx < origin_x)
    {
      //t（比例）=（地图原点-传感器原点）/（点云中的该点-传感器原点）
      double t = (origin_x - ox) / a;
      wx = origin_x;
      //当前点y = 
      //实际上还是把点云点和传感器连线之间清空，只是通过相似三角形丢弃了超出地图原点范围外的部分，下面三个判断结构同理
      wy = oy + b * t;
    }
    if (wy < origin_y)
    {
      double t = (origin_y - oy) / b;
      wx = ox + a * t;
      wy = origin_y;
    }

    // the maximum value to raytrace to is the end of the map
    if (wx > map_end_x)
    {
      double t = (map_end_x - ox) / a;
      wx = map_end_x - .001;
      wy = oy + b * t;
    }
    if (wy > map_end_y)
    {
      double t = (map_end_y - oy) / b;
      wx = ox + a * t;
      wy = map_end_y - .001;
    }

    // now that the vector is scaled correctly... we'll get the map coordinates of its endpoint
    unsigned int x1, y1;

    // check for legality just in case
    if (!worldToMap(wx, wy, x1, y1))
      continue;

    unsigned int cell_raytrace_range = cellDistance(clearing_observation.raytrace_range_);
    MarkCell marker(costmap_, FREE_SPACE);
    // and finally... we can execute our trace to clear obstacles along that line
    raytraceLine(marker, x0, y0, x1, y1, cell_raytrace_range);

    updateRaytraceBounds(ox, oy, wx, wy, clearing_observation.raytrace_range_, min_x, min_y, max_x, max_y);
  }
}

一、Bresenham算法源码解析

raytraceFreespace函数主要是将传感器和障碍物点云之间的空间均设置成freespace（即地图更新无障碍物）。

为什么要如此设置？

因为在ObstacleLayer::updateBounds函数中对障碍物处理主要分为两部分：
（1）将传感器和障碍物点云之间的空间均设置成freespace（即地图更新无障碍物）。
（2）循环遍历障碍物点云与传感器原点距离，将满足距离条件的标记为障碍物。
然后这个地图就会一直调用上述两步来更新地图。设想，如果没有第一步（将传感器和障碍物点云之间的空间均设置成freespace（即地图更新无障碍物）那会导致前有一些障碍物明明已经不存在传感器周围了但还是会存在地图中，并挡住机器人前进的道路，因此要不断迭代传感器原点和点云中的点的连线，并对其调用raytraceLine函数，并将连线上的点在本层地图上全部标记为FREE_SPACE。
至此，我应该说明白了为什么要分析这个raytraceLine函数。

1. 函数raytraceFreespace

 //wx wy是当前点云中的点的坐标
    double wx = cloud.points[i].x;
    double wy = cloud.points[i].y;

    // now we also need to make sure that the enpoint we're raytracing
    // to isn't off the costmap and scale if necessary
    //a、b是该点跟传感器原点的距离
    double a = wx - ox;
    double b = wy - oy;

    // the minimum value to raytrace from is the origin
    //如果当前点x方向比地图原点还小
    if (wx < origin_x)
    {
      //t（比例）=（地图原点-传感器原点）/（点云中的该点-传感器原点）
      double t = (origin_x - ox) / a;
      wx = origin_x;
      //当前点y = 
      //实际上还是把点云点和传感器连线之间清空，只是通过相似三角形丢弃了超出地图原点范围外的部分，下面三个判断结构同理
      wy = oy + b * t;
    }
    if (wy < origin_y)
    {
      double t = (origin_y - oy) / b;
      wx = ox + a * t;
      wy = origin_y;
    }

    // the maximum value to raytrace to is the end of the map
    if (wx > map_end_x)
    {
      double t = (map_end_x - ox) / a;
      wx = map_end_x - .001;
      wy = oy + b * t;
    }
    if (wy > map_end_y)
    {
      double t = (map_end_y - oy) / b;
      wx = ox + a * t;
      wy = map_end_y - .001;
    }

    // now that the vector is scaled correctly... we'll get the map coordinates of its endpoint
    unsigned int x1, y1;

    // check for legality just in case
    if (!worldToMap(wx, wy, x1, y1))
      continue;

上述的代码主要是考虑如果点云不在地图范围内，我们通过相似三角形丢弃了超出地图原点范围外的部分。
当点云的坐标超过了地图的边界，即超过了地图的原点和大小范围时，我们无法直接在地图中对这些点进行操作。因此，我们需要通过一种方法将这些超出地图边界的点“投影”到地图的边界上。

使用相似三角形的概念，我们可以假设点云点与传感器原点之间的连线与地图的边界有一定的相似度。通过使用传感器原点和点云点之间的距离关系，在地图的边界上找到与该连线相交的点。

具体做法是，计算点云点与传感器原点之间在x和y方向上的距离a和b。然后，通过比较原点坐标与地图边界坐标的差值，计算出比例因子t，即t = (origin_x - ox) / a 或 t = (origin_y - oy) / b。使用这个比例因子t，可以将点云点坐标更新为与地图边界上的连线相交的点。

例如，如果点云点的x坐标小于地图的origin_x，则表示点云点在地图的左侧。在这种情况下，我们将x坐标更新为地图的origin_x，然后使用相似三角形的比例因子t来计算更新y坐标，即wy = oy + b * t。通过这样的处理，我们实际上将点云点与传感器原点之间的连线部分被投影到了地图边界上。

同样地，对于点云点的y坐标小于地图的origin_y或x坐标大于地图的map_end_x或y坐标大于地图的map_end_y的情况也进行类似的处理。通过这样的方法，我们保证了光线追踪的结束点在地图边界范围内，以便对障碍物进行处理。

2. 函数inline void raytraceLine

 inline void raytraceLine(ActionType at, unsigned int x0, unsigned int y0, unsigned int x1, unsigned int y1,
                             unsigned int max_length = UINT_MAX)
    {
      int dx = x1 - x0;
      int dy = y1 - y0;

      unsigned int abs_dx = abs(dx);
      unsigned int abs_dy = abs(dy);

      int offset_dx = sign(dx);
      int offset_dy = sign(dy) * size_x_;

      unsigned int offset = y0 * size_x_ + x0;

      // we need to chose how much to scale our dominant dimension, based on the maximum length of the line
      double dist = hypot(dx, dy);
      double scale = (dist == 0.0) ? 1.0 : std::min(1.0, max_length / dist);

      // if x is dominant
      if (abs_dx >= abs_dy)
      {
        int error_y = abs_dx / 2;
        bresenham2D(at, abs_dx, abs_dy, error_y, offset_dx, offset_dy, offset, (unsigned int)(scale * abs_dx));
        return;
      }

      // otherwise y is dominant
      int error_x = abs_dy / 2;
      bresenham2D(at, abs_dy, abs_dx, error_x, offset_dy, offset_dx, offset, (unsigned int)(scale * abs_dy));
    }

这个函数用于在2D网格上使用Bresenham的线算法绘制从点(x0, y0)到点(x1, y1)的线段。线段的长度可以通过’max_length’参数进行限制。网格的宽度为size_x_。该算法计算x和y坐标的差值(dx和dy)，以确定线段的方向。然后，它计算dx和dy的绝对值(abs_dx和abs_dy)。
偏移量(offset_dx和offset_dy)用于根据线段的方向增加当前点的偏移量。初始偏移量基于起始点(y0 * size_x_ + x0)。该函数还使用hypot()函数计算起始点和终点之间的距离(dist)。根据线段的最大长度计算一个缩放因子(scale)。如果距离为0，则缩放因子为1。否则，它是1和max_length / dist的较小值。如果abs_dx大于abs_dy，表示线段更水平。在这种情况下，函数使用适用于x主导的参数执行bresenham2D()函数。如果abs_dx不大于abs_dy，表示线段更垂直（或两者都一样）。在这种情况下，函数使用适用于y主导的参数执行bresenham2D()函数。

为什么offset_dx和offset_dy定义不同？

在Bresenham算法中，我们需要确定沿着直线绘制时，在x方向和y方向上每一步的移动距离。
在x方向上移动的距离（offset_dx）是基于两个相邻的x坐标之间的差值(dx)。如果dx是正数，我们知道我们需要向右移动，因此将offset_dx设置为1；如果dx是负数，我们需要向左移动，因此将offset_dx设置为-1；如果dx是0，我们在x方向上不需要移动，因此offset_dx为0。
在y方向上移动的距离（offset_dy）是基于两个相邻的y坐标之间的差值(dy)和网格的宽度（size_x_）。由于我们在二维网格上移动，位置之间的偏移量不仅取决于dy的正负号，还取决于网格的宽度。如果dy是正数，我们需要向上移动，因此将offset_dy设置为size_x_；如果dy是负数，我们需要向下移动，因此将offset_dy设置为-size_x_；如果dy是0，我们在y方向上不需要移动，因此offset_dy为0。
这样的计算方式是为了保持在绘制线段时，在x和y方向上的每一步移动的距离是平衡的。这有助于保持线段的斜率正确，并产生平滑的绘制效果。如果两个方向上的移动步长不平衡，可能会导致线段的形状不准确或出现奇怪的绘制效果。

其实更简洁的解释就是我们这里的地图是一维数组，通过一维数组储存二维地图，如果该点在地图中的信息即为data[index]，data是按照那张地图图片的自底向上，自左至右逐个像素点存储的。因此如果向右移动就+1，向上移动就需要×地图x_size_,详细关系参考《机器人控制算法—如何使用C++读取pgm格式的栅格地图并转化为ROS地图格式的data?》中的“data[]是按照那张地图图片的自底向上，自左至右逐个像素点存储的”。

3. 函数bresenham2D

  inline void bresenham2D(ActionType at, unsigned int abs_da, unsigned int abs_db, int error_b, int offset_a,
                            int offset_b, unsigned int offset, unsigned int max_length)
    {
      unsigned int end = std::min(max_length, abs_da);
      for (unsigned int i = 0; i < end; ++i)
      {
        at(offset);
        offset += offset_a;  //unsigned int offset = y0 * size_x_ + x0;int offset_dx = sign(dx);
        error_b += abs_db;//error_b = abs(x1-x0)/2   abs_db = abs(y1-y0)
        if ((unsigned int)error_b >= abs_da)
        {
          offset += offset_b;  //offset_b = sign(dy) * size_x_;
          error_b -= abs_da;  //
           = abs(x1 - x0);
        }
      }
      at(offset);
    }

这个函数实现了Bresenham的直线绘制算法，用于在二维网格上绘制直线。
函数有以下参数：

at: 表示要执行的操作类型，可以是函数、函数指针或可以使用函数调用运算符()的函数对象。
abs_da和abs_db: 表示x和y方向上的绝对差值（dx和dy的绝对值）。
error_b: 表示y方向上的误差值。
offset_a和offset_b: 表示在x和y方向上的偏移量。
offset: 表示当前点的偏移量，即当前要绘制的网格位置。
max_length: 表示线段的最大长度。
算法工作原理如下：

首先，确定了直线上需要绘制的点的个数，即end = min(max_length, abs_da)。取较小值是为了确保在达到最大长度或直线的实际长度之前停止绘制。
然后，通过一个循环迭代来绘制直线。循环的次数为end。
在循环体内，首先调用at函数来对当前点进行操作或绘制。然后，将offset增加offset_a表示在x方向上移动一步。
接下来，将error_b增加abs_db表示在y方向上移动一步。
判断error_b的绝对值是否大于等于abs_da。如果成立，说明在y方向上的移动超过了x方向上的移动距离。此时，将offset再增加offset_b，表示在y方向上进行一次额外的移动。然后，将error_b减去abs_da，以更新误差值。
循环重复以上步骤，直到达到终点end。
绘制结束后，再次调用at函数对最后一个点进行操作或绘制。

这个算法通过根据斜率的比例，在x和y方向上以平衡的步长移动，从而在二维网格上绘制出准确和平滑的直线。

在第5步中，我们判断error_b的绝对值是否大于等于abs_da，以确定是否需要在y方向上进行额外的移动。
假设我们正在绘制一条斜率小于1的直线，此时直线的在x方向上的增量大于y方向上的增量。在直线绘制过程中，每绘制一个像素点，在x方向上总是前进1个像素，而在y方向上可能需要前进0个或1个像素。

为了决定是否在y方向上进行额外的移动，我们需要比较y方向上的误差（error_b）和x方向上的增量（abs_da）的大小关系。如果误差超过或等于增量，说明在y方向上需要进行额外的移动。

具体的步骤如下：

判断error_b的绝对值是否大于等于abs_da：
- 如果是（error_b >= abs_da），说明在y方向上的误差已经超过或等于了x方向上的增量。
- 这表示绘制的点已经超过了直线在x方向上的应有长度，因此需要在y方向上进行额外的移动。
如果需要在y方向上进行额外的移动：
- 将offset再增加offset_b，表示在y方向上进行一次额外的移动。
- 将error_b减去abs_da。这样可以更新误差值，使得误差包含了在y方向上多余移动所产生的部分。
继续循环，绘制下一个点。

通过使用这个方法，在直线绘制过程中，我们可以根据误差和增量的关系，确保在y方向上进行恰当的额外移动，以准确地绘制出直线。这也是Bresenham算法的关键所在，它使得绘制的直线更接近理想情况下的连续直线。

怎么理解error_b?
误差error_b在Bresenham算法中用于帮助决定在y方向上是否需要额外移动。

在绘制直线的过程中，我们需要根据每一步的x方向的移动来决定是否在y方向上进行额外移动。而误差error_b的作用就是跟踪y方向上的累积误差。

具体来说，对于每一步在x方向上的移动，我们将误差error_b加上y方向上的增量abs_db。这个增量表示经过一次x方向上的移动后，y方向上实际移动的距离。

当误差累积到超过或等于x方向上的增量abs_da时，我们知道在y方向上已经超过了应有的移动量。这意味着在绘制直线时需要在y方向上进行额外移动。

例如，考虑绘制一条斜率小于1的直线。在每一步中，我们通过在x方向上移动1个像素来绘制直线，并将误差error_b加上y方向上的增量abs_db。当误差error_b超过或等于x方向上的增量abs_da时，说明在y方向上需要额外移动。

通过跟踪误差error_b，我们能够准确地判断是否需要在y方向上进行额外移动，以实现精确绘制直线的目的。

error_b初值怎么确认？
误差error_b的初始值应该根据直线的起始点和终止点的坐标差值来计算。

在Bresenham算法中，我们通过比较x方向和y方向的差值来确定每一步的移动方向。因此，我们可以利用起始点和终止点的坐标差值来初始化误差error_b，以确保正确的绘制路径。

具体设置error_b初始值的步骤如下：

计算|dy| - |dx|的值，其中dy表示终止点的y坐标减去起始点的y坐标，dx表示终止点的x坐标减去起始点的x坐标。
将计算结果赋值给error_b，作为初始误差值。

这样设置初始值的目的是为了根据斜率的大小关系来决定每一步在x方向和y方向上的移动。

如果|dy| > |dx|，即直线的斜率大于1，说明直线在y方向上的变化较大，因此我们期望在y方向上移动更远。通过将初始误差值设置为|dy| - |dx|，我们能够正确初始化误差，使其适应y方向上的更大变化。

如果|dy| <= |dx|，即直线的斜率小于等于1，说明直线在x方向上的变化较大或两者相等。由于我们每次在x方向上移动1个像素，因此不需要在初始误差值中考虑x方向上的差异。

需要注意的是，根据直线的起始点和终止点的不同，可能需要将初始误差值设置为正值或负值，以确保在正确的方向上进行绘制。

通过进行正确初始化的误差error_b，我们可以在Bresenham算法中正确追踪和利用误差值，从而绘制出准确和平滑的直线。

二、Bresenham算法——C++代码实现

当使用Bresenham算法绘制直线时，我们考虑的是从起始点到终止点的直线段，我们希望找到合适的格点来近似这条直线。
Bresenham算法的主要思想是通过比较斜率的大小和符号来确定如何在x方向和y方向上前进。算法依赖于以下几个主要步骤：‘

将起始点的坐标 (x0, y0) 作为当前点的坐标 (x, y)。
计算起始点到终止点的差值 dx = x1 - x0 和 dy = y1 - y0。
计算绝对差值的绝对值 abs_dx = |dx| 和 abs_dy = |dy|。
初始化误差值 error 为0。
根据斜率的比例来决定是在x方向上前进还是在y方向上前进。

如果 abs_dx >= abs_dy，那么直线与水平方向的夹角较小或相等。我们在x方向上前进1个像素，并更新误差值 error。
- 如果 dx > 0，则 x 增加1，表示向右移动。
- 如果 dx < 0，则 x 减少1，表示向左移动。
- 如果 dx = 0，则 x 保持不变，表示在x方向上不移动。
- 更新误差值：error += abs_dy。
如果 abs_dx < abs_dy，那么直线与竖直方向的夹角较小。我们在y方向上前进1个像素，并更新误差值 error。
- 如果 dy > 0，则 y 增加1，表示向上移动。
- 如果 dy < 0，则 y 减少1，表示向下移动。
- 如果 dy = 0，则 y 保持不变，表示在y方向上不移动。
- 更新误差值：error += abs_dx。

在每一步中，我们都会绘制当前点 (x, y)。这可以是在网格上进行某种操作，如绘制像素或修改像素值。
重复上述步骤，直到达到终止点 (x1, y1)。

通过根据斜率的比例选择正确的前进方向，并将误差值考虑在内，Bresenham算法找到了在离散网格上绘制直线的最佳路径。这种算法的优势是，它避免了使用浮点运算并使用了整数运算，因此具有更高的效率和性能。

/*面是将 bresenham2D 函数进行注释并且编写一个简单的 C++ 小 demo 来演示它的用法：

```cpp
*/
#include <iostream>
using namespace std;
// ActionType 是一个函数类型，用于在每个点上执行特定的操作
typedef void (*ActionType)(unsigned int);

// bresenham2D 函数用于绘制直线
void bresenham2D(ActionType at, unsigned int abs_da, unsigned int abs_db, int error_b, int offset_a,
                 int offset_b, unsigned int offset, unsigned int max_length)
{
  // 计算需要绘制的点的个数（取 max_length 和 abs_da 之间较小的值）
  unsigned int end = std::min(max_length, abs_da);
  
  // 循环绘制每个点
  for (unsigned int i = 0; i < end; ++i)
  {
    // 在当前点上执行特定的操作
    at(offset);
    //cout << "offset:"<<offset<<endl; 
    // 根据offset_a进行 x 方向上的移动
    offset += offset_a;

    // 更新 error_b，用于判断是否需要进行 y 方向上的额外移动
    error_b += abs_db;
    //cout << "error_b ="<<error_b<<endl;
    //cout << "abs_db ="<<abs_db<<endl;
    //cout << "abs_da ="<<abs_da <<endl;
    // 如果 error_b 的绝对值大于等于 abs_da，表示需要进行 y 方向上的额外移动
    if ((unsigned int)error_b >= abs_da)
    {
      // 在 offset 上进行 y 方向上的偏移
      offset += offset_b;

      // 更新 error_b，去除额外移动后剩余的误差
      error_b -= abs_da;
    }
  }

  // 绘制最后一个点
  at(offset);
}

// 示例操作：打印当前点的坐标
void printPoint(unsigned int offset)
{
  unsigned int x = offset % 10;
  unsigned int y = offset / 10;
  std::cout << "Point: (" << x << ", " << y << ")" << std::endl;
}

int main()
{
  // 设置将要绘制直线的参数
  unsigned int x0 = 2, y0 = 1;
  unsigned int x1 = 8, y1 = 4;
  unsigned int max_length = 10;

  // 使用 bresenham2D 绘制直线，并在每个点上打印坐标
  bresenham2D(printPoint, x1 - x0, y1 - y0, 0, 1, 10, y0 * 10 + x0, max_length);
  //bresenham2D(ActionType at, unsigned int abs_da, unsigned int abs_db, int error_b, int offset_a,
                 //int offset_b, unsigned int offset, unsigned int max_length)
  //abs_da = x1 - x0;abs_db = y1 - y0;error_b = 0;offset_a = 1; 
  //offset_b = 10;offset =  y0 * 10 + x0;max_length = 10
  return 0;
}
/*
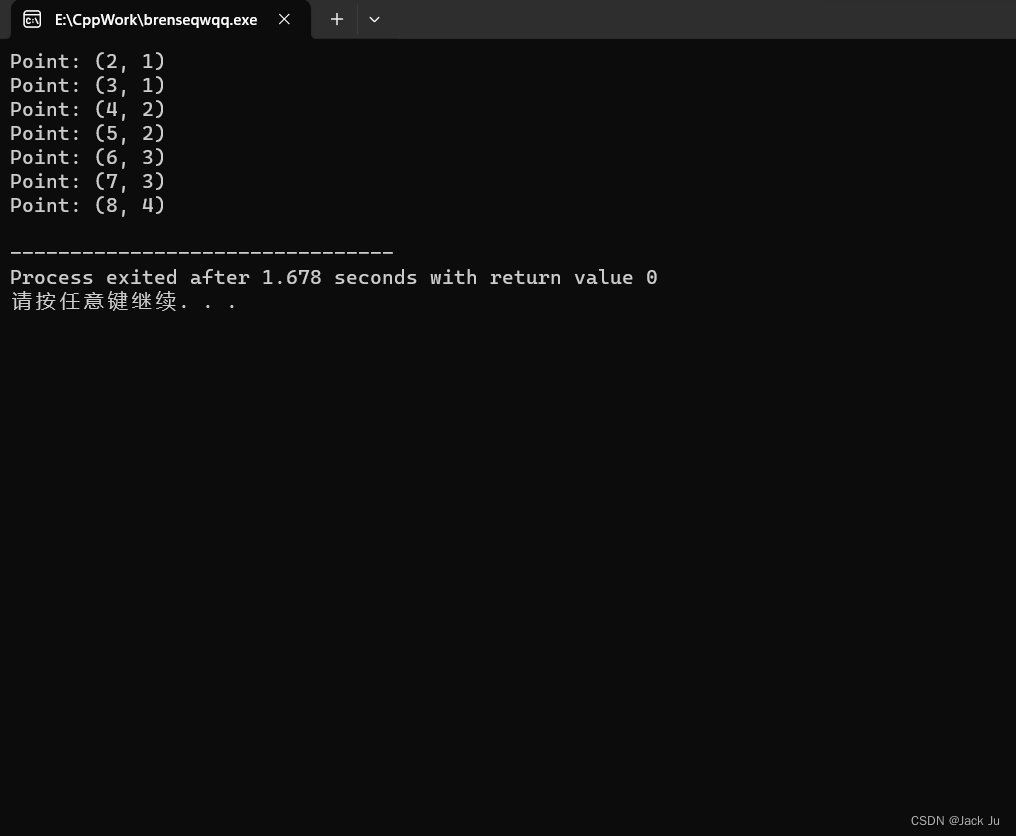
 显然这是以x为主导的例子。 
这个代码演示了如何使用 `bresenham2D` 函数来绘制直线，并在每个点上执行特定的操作
（在这个例子中是打印点的坐标）。你可以根据需要定义和传入其他的 `ActionType` 函数，来执行不同的操作。
*/