任务一:
复现环境中的漏洞
任务二:
上传webshell或者反弹shell,并执行whoami。
任务一:
1.环境搭建,发现需要密码,所以我们去日志里面查看管理员密码。
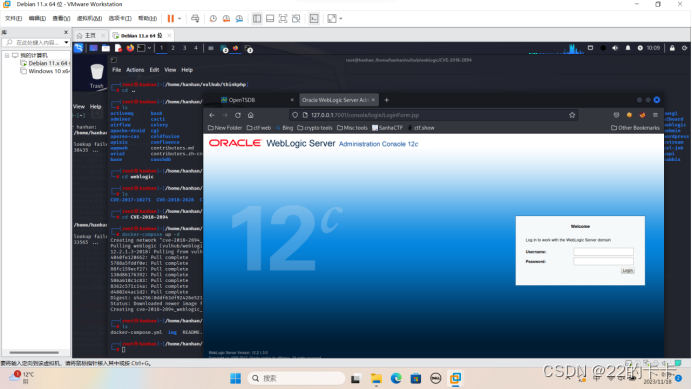
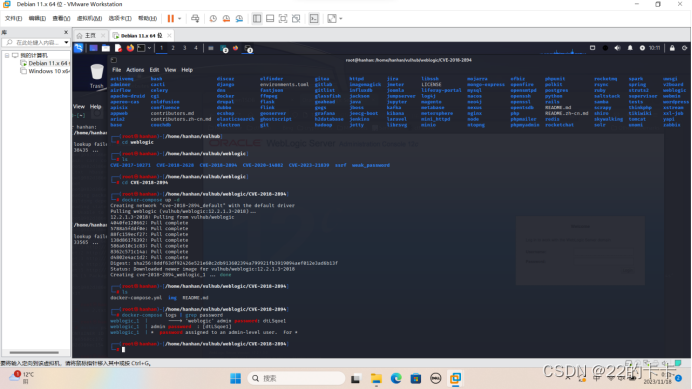
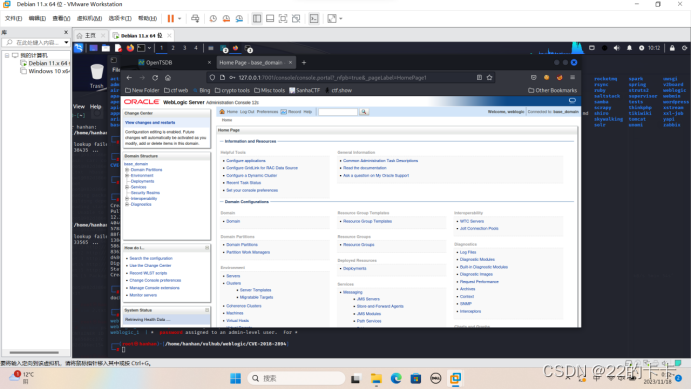
2.了解一下这个平台,然后进行一些基本配置
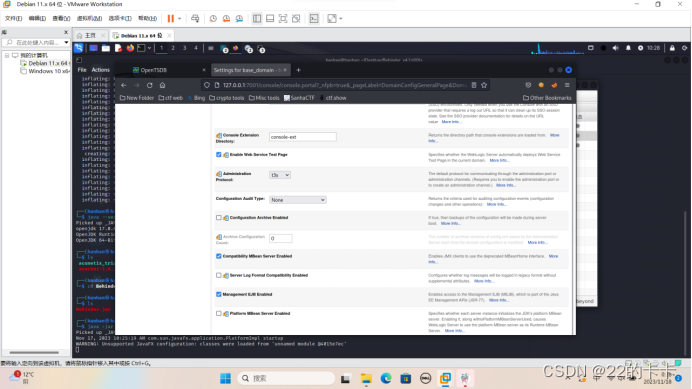
3,访问127.0.0.1/ws_utc/config.do,然后将工作目录设置成不需要权限的文件目录。
3.上传冰蝎木马,看到别人的复盘好像需要时间戳,还得抓个包,在上传的时候抓包,然后看到自己上面的时间戳。

4.终于连上了(这里后面重新抓爆了很多次,因为一直连不上,后来发现,是那个密码写错了,密码的提示在抓包的包里面写了,之前不知道,一直在输入自己的123456)
5.然后反弹shell出来了。
6.执行whoami