完全二叉树(Complete Binary Tree)是一种特殊的二叉树结构,它具有以下特点:
- 所有的叶子节点都集中在树的最后两层;
- 最后一层的叶子节点都靠左排列;
- 除了最后一层,其他层的节点数都达到最大值。
满二叉树(Full Binary Tree),又称为真二叉树,是一种特殊的完全二叉树结构,它具有以下特点:
- 所有的叶子节点都在同一层;
- 每个非叶子节点都有两个子节点;
- 所有节点的子节点数都为0或2。
满二叉树是完全二叉树的一种特殊情况,每个非叶子节点都有两个子节点,而完全二叉树可以有一个或没有一个子节点。
树的定义,遍历,输入构建,一些递归复习(求叶子节点,数的高度)
ABC##DE#G##F###
5
第二次实验——二叉树中序遍历
ABD##FE###CG#H##I##
DBEFAGHCI
第十一周,后序+中序确定二叉树
树的性质
第二次实验的思考题

一棵非空二叉树,若后序遍历与中序遍历的序列相同,则该二叉树所有结点均无右孩子。
非空的二叉树一定满足:某结点若有左孩子,则其中序前驱一定没有右孩子。
二分查找法
二叉搜索树复习
寻找公共祖先
排序算法
第二次实验——快速排序的过程
5
4 5 3 2 1
输出
2 1 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
插入排序还是归并排序
10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0
Insertion Sort
1 2 3 5 7 8 9 4 6 0
10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6
Merge Sort
1 2 3 8 4 5 7 9 0 6
插入排序,冒泡排序,选择排序,堆排序,归并排序
第八周习题——冒泡排序
第九周习题——二路归并排序
归并排序,逆序对
第七周——插入排序
结构体排序
第九周习题——成绩排名
第八周习题——小球装箱
排序算法性质
合并排序算法是稳定的排序方法。


直接插入排序在最好的情况下时间复杂度为O(n)

直接插入排序是稳定的
逆序对,倍数对
堆的调整,构建
调整
void shiftup(int child) {//在末尾插入一个孩子,然后就这个孩子一直往上调整,这样的话调整路径都满足堆的性质
int parent = (child - 1) / 2;
while (child > 0) {
if (arr[parent] > arr[child]) {
break;
}
else {
swap(arr[parent], arr[child]);
child = parent;//往上调整一步
parent = (child - 1) / 2;//这里是先调整了孩子指针,所以这时候的父母就是父母的父母
}
}
}
void shiftup(int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (arr[parent] > arr[child]) { break; }//大顶堆,上面大,就不调整了
else {
swap(arr[parent], arr[child]);
child = parent;
parent = (child - 1) / 2;
}
}
}
//向上调整的话就是找到最后一个孩子,然后找到它的父母节点,孩子对应的父母节点是唯一的,所以可以直接比较
//直接比较完后直接交换,直到到底
//向下调整的话就是先找到堆顶元素,然后由于堆是完全二叉树,所以对应两个孩子,找到最小的孩子,然后调整
//调整后,使被调整的孩子作为父母节点,找到其左孩子节点
//即,向上调整只需要找到一个节点信息,即当下节点信息,就可以确定父母节点,单向比较即可
//而向下调整需要两个节点信息,一个是当下节点信息(父母节点),还要直到它是否有孩子,默认为左孩子,然后判断一下有没有右孩子
//由此向下递归进行需要两个信息,一个父母节点,一个孩子节点,递归时默认孩子节点为左孩子,2*cur+1,然后尝试找右孩子
//如果在下次递归时,左孩子越界,那就说明此时父母节点已是叶子节点,到底了,无法继续调整。
void shiftdown(int[]arr, int size, int parent) {
int child = parent * 2 + 1;
while (child < size) {
if (child + 1 < size && arr[child + 1] > arr[child]) {
child += 1;
}
if (arr[parent] < arr[child]) {
swap(arr, parent, child);
parent = child;//由此,完成向下移动,
child = parent * 2 + 1;//孩子与父母指针都向下移动
}
else {
return;
}
}
}void shiftdown(int[]arr, int parent) {//父母直接,指向要交换的元素
int child = 2 * parent + 1;//孩子指针,指向要交换的元素
int size = arr.length();
while (child < size) {//只要有这一步,就说明当下节点至少存在左孩子
if (child + 1 < size && arr[child + 1] < arr[child]) {
child += 1;//如果向右一个单位存在,就说明当下节点有右孩子,找最小的
}//确定较小的孩子
if (arr[parent] <= arr[child]) {
break;
}
else {
int t = arr[parent];
parr[parent] = arr[child];
arr[child] = t;
parent = child;
child = parent * 2 + 1;
}
}
}如果左孩子存在,则child<size,不断进行操作,直到左孩子不存在
检测右孩子是否存在,找左右孩子中最小的孩子
堆的创建
这个就是先输入,输入一个数组,输入完后再开始调整,从最后一个非叶子结点开始,然后不断往上往回走,进行向下调整
public static void createHeap(int[] array) {
// 找倒数第一个非叶子节点,从该节点位置开始往前一直到根节点,遇到一个节点,应用向下调整
for(int root = (array.length-2)/2; root >= 0; root--){
shiftDown(array, array.length, root);
}
}插入,边插边保持堆
int arr[100];
int siz = 0;
void shiftup(int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (arr[parent] >= arr[child]) {
break;
}
else {
swap(arr[parent], arr[child]);
child = parent;
parent = (child - 1) / 2;
}
}
}
void insert(int num) {
arr[siz++] = num;
shiftup(siz - 1);
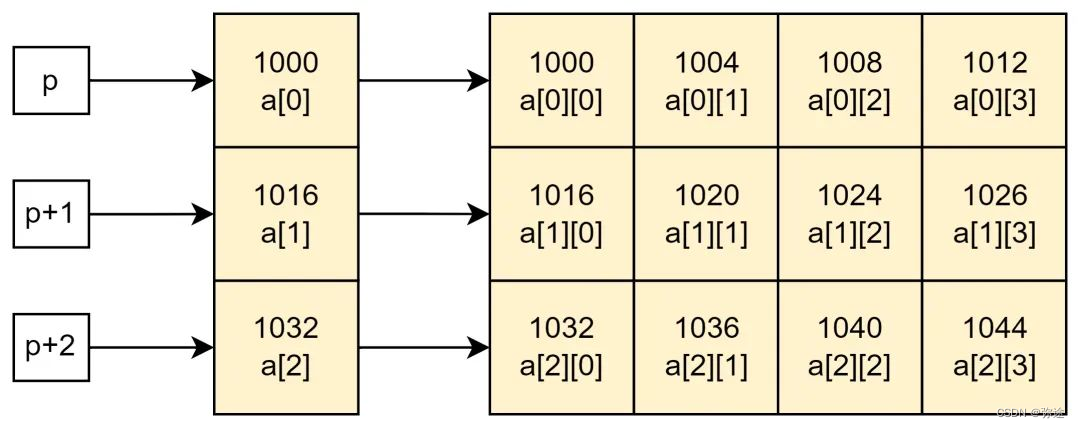
}二叉树指针关系
对于二叉树的孩子双亲指针指引,如果是从1开始记录的,那么
左孩子结点索引 = 2 * i 右孩子结点索引 = 2 * i + 1
其中,i表示当前结点的索引位置。
当索引从1开始记录时,根节点的索引为1,其左孩子结点的索引为2,而右孩子结点的索引为3。对于任意结点i,其左孩子结点的索引位置为2 * i,右孩子结点的索引位置为2 * i + 1。
如果是从0开始记录的,
二叉树以数组形式存储时,一般约定根节点的索引位置为0,其左孩子结点的索引位置为1,右孩子结点的索引位置为2。对于任意结点i,其左孩子结点的索引位置为2 * i + 1,右孩子结点的索引位置为2 * i + 2。
堆的一些性质
下标从0开始计数的堆,大小为size时,其最后一个非叶子结点是(size-2)/2;
最后一个叶子结点的下标为size-1.
由于是下标从0,所以对结点i而言,其双亲结点下标为(i-1)/2
(如果下标从1开始,那么整体往右偏移一位)
所以对于下标为size-1的结点,它的双亲结点为(size-1-1)/2;
最大堆(大顶堆、max-heap)从根结点到其它任一结点的路径上的所有结点值是从大到小排列的。

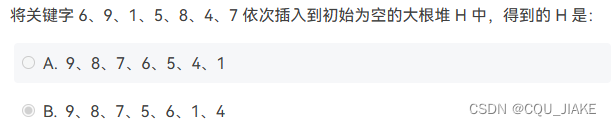
第十二周堆的操作,堆的建立