2023.11.29 深度学习框架理解

对深度学习框架进行复习，选最简单的“三好学生”问题的四个变化，简要总结其具体思路。

深度学习一开始就是为分类问题研究的，因此其框架的设计都是基于分类的问题，虽然现在也已经演变为可以执行多种问题。
目前学习到的深度学习框架实际上分为两部分：正向传播和反向传播。

1. 正向传播

一般基于 y=wx+b 样式的数学架构，即假设对于一切的事物（ y ）都是可以用数学公式表示的，当然对于哲学家来说，能用数学表示的世界才是美的。因此深度学习的方法的本质就是找到各个 w ，即每个参数 x 之间的权重关系。对于 b ，由于其实际上是一个固定参数，所以并不需要将其看成一个变量。反过来过任何计算方法都应该有其合理性和可解释性。

2. 反向传播

如何评价模型的好坏，最简单的办法就是看结果与实际值偏差的大小，比如（y-y预测）的绝对值，即损失函数，模型计算的最终目的就是让损失函数最小，为达到这个目的，可以采用梯度下降法或其衍生的多种计算不断地对正向传播的计算结果进行损失函数的计算，并将计算结果反馈到正向传播的过程中，从而去修正最终的计算结果。

3. 学习率

学习率决定每次反向传播算法的“步长”，即每次计算结果的变化幅度，如果学习率太小，学习结果收敛太慢，学习率太大，则有可能一下就跨过最优解，从而无法获得最佳的计算结果。

4. 基础案例

案例1:最简单的深度学习模型（“三好学生”问题）

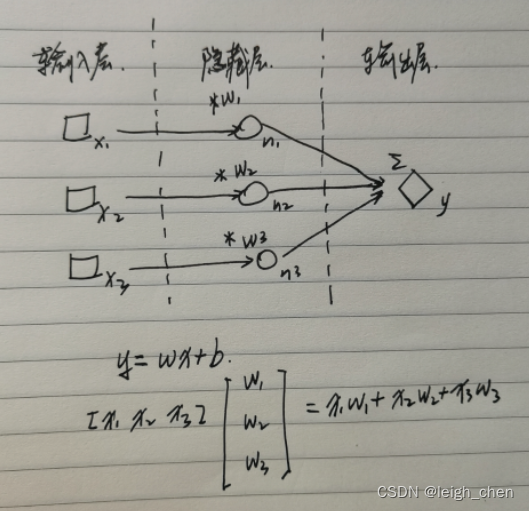
如下图，例如对“三好学生”问题，假设知道某学生三门科目的真实成绩和学校提供的综合成绩，但是并不知道学校是以什么权重对三门科目进行计算获得综合成绩的。即x1，x2，x3和y是已知的，求解w1，w2，w3。这个问题实际上只要有三组分数就能直接列方程组计算出来，因此是个最简单的数学模型，该问题是一个线性问题。深度学习的作用相当于是在仅有一组数据的情况下，最快找到w1，w2，w3。

计算机为了找到w1，w2，w3，可以选择穷举法，但是在多变量下这个方法计算量会非常大，加入反相传播进行求解，能将运算简化，即便使用反向传播算法，仍然要经过大量的计算。因此深度学习是以大数据和大计算量为基础的。

另外从数学关系上可知，w1，w2，w3作为权重变量，三者之和应为 1 ，因此可以用tf.nn.softmax对w1，w2，w3进行约束，相对于多了一个方程，即 w1+w2+w3=1，要注意的是该方法只有在 x1，x2，x3 能完全描述 y 的时候使用才能获得正确的结果。例如同样是“三好学生”，如果仅提供两个科目的成绩，使用该方法就与现实逻辑不符。数据多没有影响，可以认为多出的参数权重为 0 ，现实是大部分情况下，我们并不知道自己拥有的参数是否能对事物进行一个完整的描述。因此我们一般都假设这个做法是正确的，这个方法在各个参数权重比较明确的情况下运行良好。如果权重并不明确，模型也有可能收敛，但是并不能获得一个比较好的精度。所以tf.nn.softmax一般用在分类结果的预测。类别是人为定义的，相对来讲存在逻辑问题较小。当然如果训练集分类有误，对结果的影响也比较大。
在这里插入图片描述

案例2:“三好学生”问题提升版

将“三好学生”问题难度提升，只给出多组的学生的成绩，即多组 x1，x2，x3 ，和他们是否是“三好学生”的结论，但是不提供 w1，w2，w3 和 y 。另外前面的问题中，只是给出了综合成绩，但是具体综合成绩达到多少分以上才是“三好学生”并没有给出这个标准，这个时候该问题就不能单纯通过数学计算活动，另外这个问题变成一个离散问题。需要引入激活函数的概念。框架变化如下图。
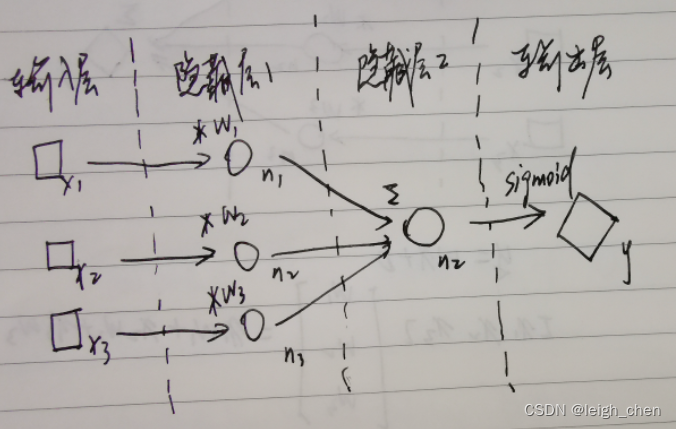
在这里插入图片描述

激活函数
深度学习算法对于线性问题的处理效果较好，这是由其模型决定的，因此对于非线形问题，需要引入激活函数。例如本例，实际上两个类别的分布并不是线形的。

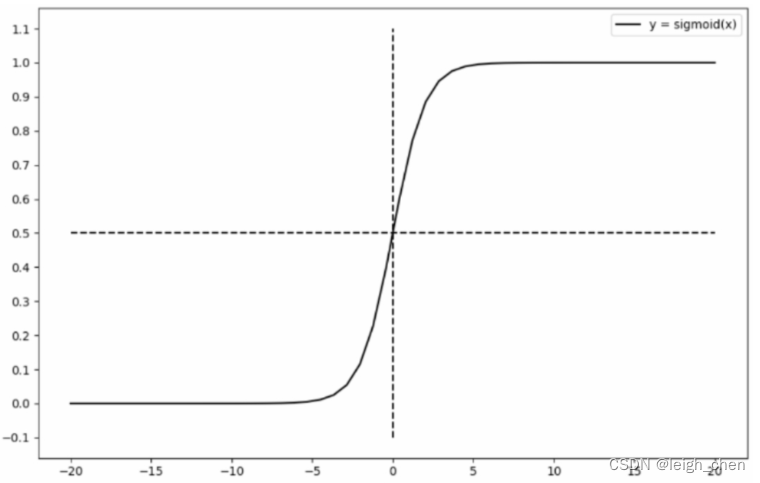
激活函数有很多种，但是本质是一样的，都是使计算结果 y 在一定的数值范围内产生较大的变化范围，而在该范围以外，基本处于固定值。例如sigmoid激活函数。如下图。其在（-5，+5）之间有较大的变化，而在这个范围以外，就是 0 和 1 ，即通过数据阶跃，实现了对结果的分类。对二值化的问题该框架有效。

而这个阶跃函数，在“三好学生”问题上，体现的实际就是具体综合成绩达到多少分以上才是“三好学生”的标准。
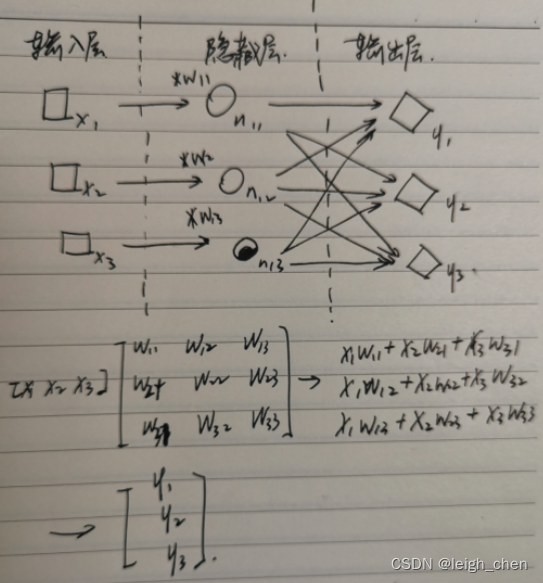
在这里插入图片描述

案例3:“三好学生”问题再次提升难度，增加“双优学生”评选

这个时候相当于有三分类的问题，分为“三好学生”，“双优学生”，“普通学生”三种，同样仅给出所有学生的三科成绩和部分学生的具体类别，要求对剩余学生的类别进行预测。计算框架如下，可以看出该框架实际上是求出了三组权重，分别是 [w11，w21，w31] 、[w12，w22，w32] 、 [w13，w23，w33]，计算原理同之前的两个案例，求出的三个类别 [y1，y2，y3] 可以用tf.nn.softmax将三者的概率之和设置为1，预测结果选择其中概率最大的一项即可。
在这里插入图片描述

另外两分类的模型也可以用这个形式去写，只是没有必要。两分类问题输出不是 1 就是 0 ，因此求出两组权重并没有意义，比如非“三好学生”，实际上计算的权重也是同“三好学生”一样的，不是“三好学生”就是非“三好学生”，如果有两组权重，有可能就会出现在这权重以外，即不是“三好学生”，又不是非“三好学生”的情况，这个就和现实情况不符合了。当然这个问题可以用tf.nn.softmax将两者的概率之和设置为1，规避上述的问题。

总而言之，更多的分类也可以使用这个方法，这个方法的本质就是各个分类求取权重，如果数据足够多，运算次数足够多，就能获得较理想的结果。简化来说实际上也是二分类问题，例如求解 y1 ，实际上可以看成先求 y1 和非 y1 两种类型。其余类别同理。因此这个方法就存在需要大量运算的缺点。

以上三个案例都是单层神经网络的计算。

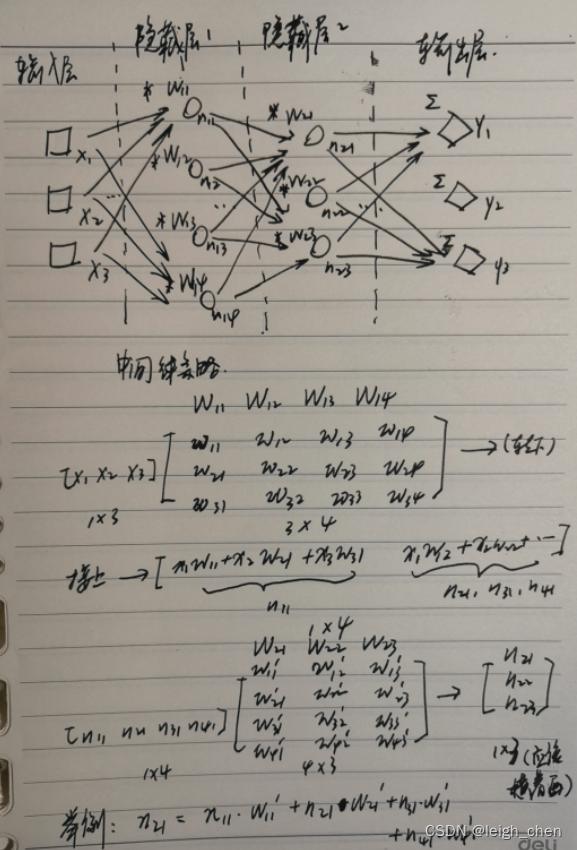
案例4:全链接算法

前面三个算法都是基于 y=wx+b 模型，很显然，现实情况并不是所有关系都能用一次方的公式去解释，因此需要使用全链接算法。可以看到这个方法真是比较天才的想法，原有基础的深度学习模型，相当于将隐藏层的行数作为神经元的个数，而使用全链接法后相当于列数作为神经元的个数，灵活运用矩阵的计算方法，使得神经元数量得到有效的提升，并可以扩展隐藏层的数量。对于前三个案例的简单模型，实际上也可以增加多个多个隐藏层，但是隐藏层的神经元数量受输入层数量的限制，当然也可以变通，第二个隐藏层参考全链接的方法，提升神经元的数量，但是如果要这样操作，直接在第一步就这样进行即可，即一开始就使用全链接的方式。全链接的模型将模型变换成 y=w^n *x+b ，即 w 不再是一次方，而可以是多次方。如果调整一下变量，可以看到公式变为 y=x * w^n+b ，这个方程就很熟悉，变成一个w的 n 元多次方程，x 是已知量，相当于系数。（这个描述只是为了便于理解，数学上不严谨，矩阵也不能这样调换位置），通过一个多元多次方程，在描述世界上是可行的。历史上很多数学大神都用各种公式，比如拉格朗日方程等描述过世界。因此理论上神经元的数量远多，层数越深，最终的预算结果就越好。

与单层神经网络不同。理论证明，两层神经网络可以无限逼近任意连续函数。
在这里插入图片描述