位图和布隆过滤器
- 一、位图
- 1. 引入
- 2. 概念
- 3. 代码实现
- set
- reset
- 完整代码
- 4. 位图的应用
- 二、布隆过滤器
- 1. 引入
- 2. 概念
- 3. 逻辑结构
- 4. 特点
- 5. 代码实现
- 6. 布隆过滤器的应用
- 三、哈希切割
一、位图
1. 引入
当面对海量数据需要处理时,内存不足以加载这些数据,这时普通的方法就不适用了。如果在这海量的数据是否存在,那么只判断状态只需要一个bit位即可,0就是不存在,1就是存在。
2. 概念
每一位都用来存放某种状态,适用于海量的数据,数据无重复的场景。通常是判断某个数据是否存在。
3. 代码实现
位操作
- |
1 | 0 = 1
1 | 1 = 1
0 | 1 = 1
0 | 0 = 0- &
1 & 0 = 0
1 & 1 = 1
0 & 1 = 0
0 & 0 = 0
set
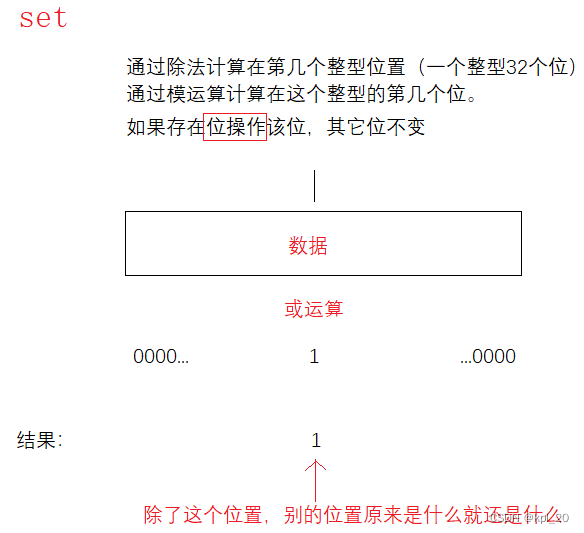
//把x映射的位置设为1
void set(size_t x)
{
int i = x / 32;
int j = x % 32;
_a[i] |= (1 << j);
}
reset

//把x映射的位置设为0
void reset(size_t x)
{
int i = x / 32;
int j = x % 32;
_a[i] &= ~(1 << j);
}
完整代码
namespace kpl
{
template<size_t N>
class bitset
{
public:
bitset()
{
_a.resize(N / 32 + 1);
}
//把x映射的位置设为1
void set(size_t x)
{
int i = x / 32;
int j = x % 32;
_a[i] |= (1 << j);
}
//把x映射的位置设为0
void reset(size_t x)
{
int i = x / 32;
int j = x % 32;
_a[i] &= ~(1 << j);
}
bool test(size_t x)
{
return _a[x / 32] & (1 << (x % 32));
}
private:
vector<int> _a;
};
}
4. 位图的应用
问题1:给定100亿个整数,计算只出现一次的数
问题2:找出现次数超过两次的所以整数
解答:可以使用两个位图控制,或者一个位图两个标志位控制
两个位图代码的实现:
namespace kpl
{
template<size_t N>
class twobitset
{
public:
//把x映射的位置设为1
void set(size_t x)
{
//00 --> 01
if (!_bs1.test(x) && !_bs2.test(x))
{
_bs2.set(x);
}
//01 --> 10
else if (!_bs1.test(x) && _bs2.test(x))
{
_bs1.set(x);
_bs2.reset(x);
}
}
bool is_one(size_t x)
{
return !_bs1.test(x) && _bs2.test(x);
}
private:
bitset<N> _bs1;
bitset<N> _bs2;
};
}
二、布隆过滤器
1. 引入
客户端推荐新内容,每次推荐要过滤掉已经存在的历史记录。如果使用哈希表,太浪费空间。单独使用位图又不能除了字符串。
所以采用位图和哈希结合的方法即布隆过滤器。
2. 概念
布隆过滤器是一种概率性数据结构,使用多个哈希函数,将一个数据用多个哈希函数映射到一个位图结构中,因此被映射的位置的比特位一定为1。
- 查找
分别计算每个哈希值对应的比特位存储是否为0,只要一个为0,则该元素一定不存在,否则可能存在在哈希表中(布隆过滤器对存在有误判)- 删除
不能直接支持删除工作,因为可能会影响其他的元素
可以通过计数器来增加这一删除操作,但是会增加几倍的存储空间,同时因为不确定该元素是否存在,可能会误删。
3. 逻辑结构
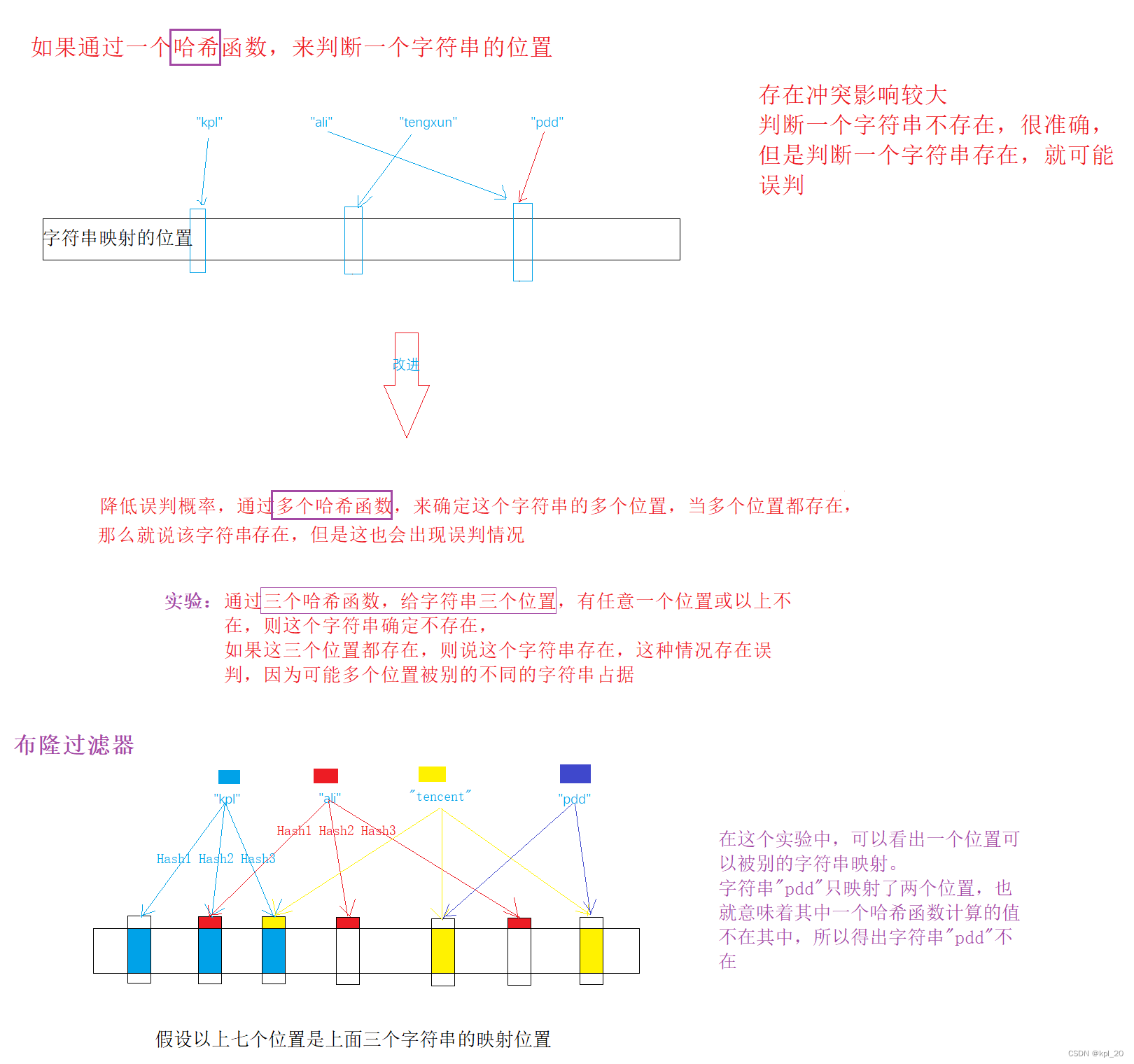
4. 特点
优点:
- 增加和查询元素的时间复杂度为O(K)(K为哈希函数的个数)
- 哈希函数相互之间没有关系
- 布隆过滤器不需要存储元素本身,保密工作更好
- 有很大大的空间优势
缺点
- 存在误判,不能准确判断元素是否在集合中。(再建立白名单,保存不确定数据)
- 不能获取元素本身
- 一般不能删除元素
5. 代码实现
#include <bitset>
#include <string>
#include <vector>
//哈希函数
struct BKDRHash
{
size_t operator()(const string& str)
{
size_t hash = 0;
for (auto ch : str)
{
hash = hash * 131 + ch;
}
return hash;
}
};
struct APHash
{
size_t operator()(const string& str)
{
size_t hash = 0;
for (size_t i = 0; i < str.size(); i++)
{
size_t ch = str[i];
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
};
struct DJBHash
{
size_t operator()(const string& str)
{
size_t hash = 5381;
for (auto ch : str)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
//布隆过滤器实现
template<size_t N,
class K = string,
class Hash1 = BKDRHash,
class Hash2 = APHash,
class Hash3 = DJBHash>
class BloomFilter
{
public:
void Set(const K& key)
{
size_t hash1 = Hash1()(key) % N;
_bs.set(hash1);
size_t hash2 = Hash2()(key) % N;
_bs.set(hash2);
size_t hash3 = Hash3()(key) % N;
_bs.set(hash3);
}
//存在误判
bool Test(const K& key)
{
return _bs.test(Hash1()(key) % N) && _bs.test(Hash2()(key) % N) && _bs.test(Hash3()(key) % N);
}
private:
bitset<N> _bs;
};
6. 布隆过滤器的应用
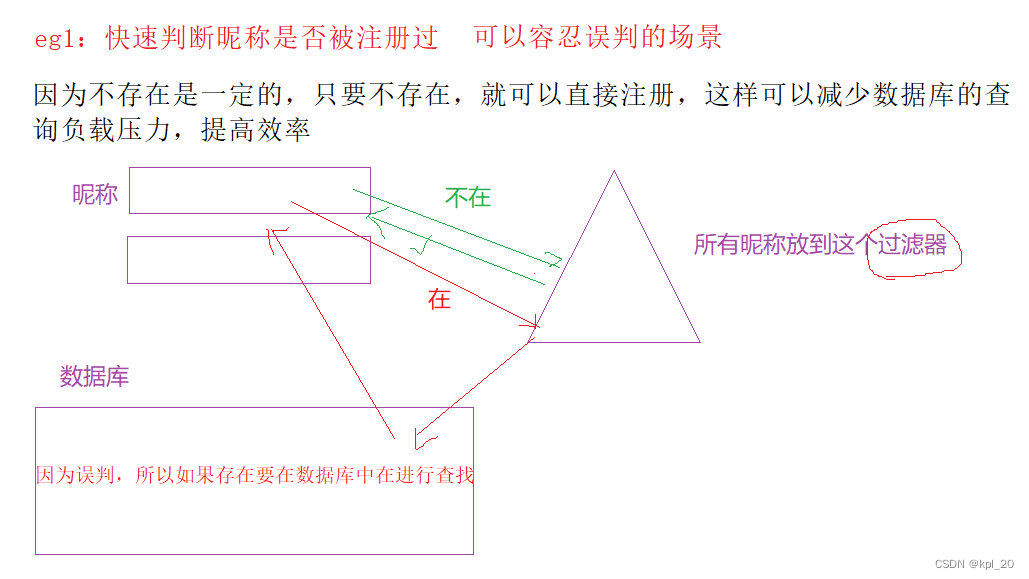
三、哈希切割
给两个文件,分别有100亿个query,我们只要1G内存,如何寻找两个文件的交集?
答:







![tornado模版注入 [护网杯 2018]easy_tornado 1](https://img-blog.csdnimg.cn/direct/df03d01c32bf482cb08b638156918029.png)