Problem: 295. 数据流的中位数

题目描述

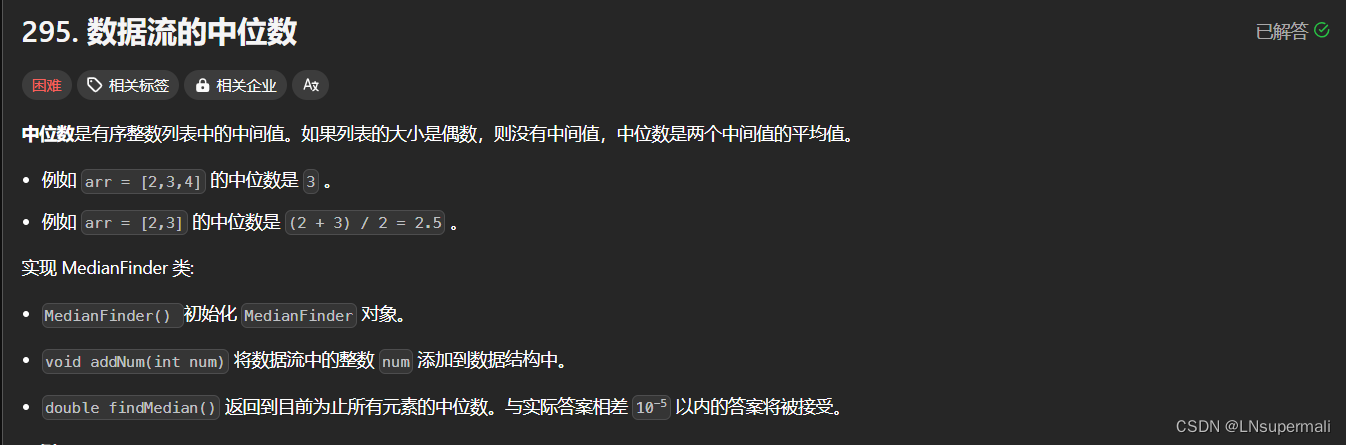
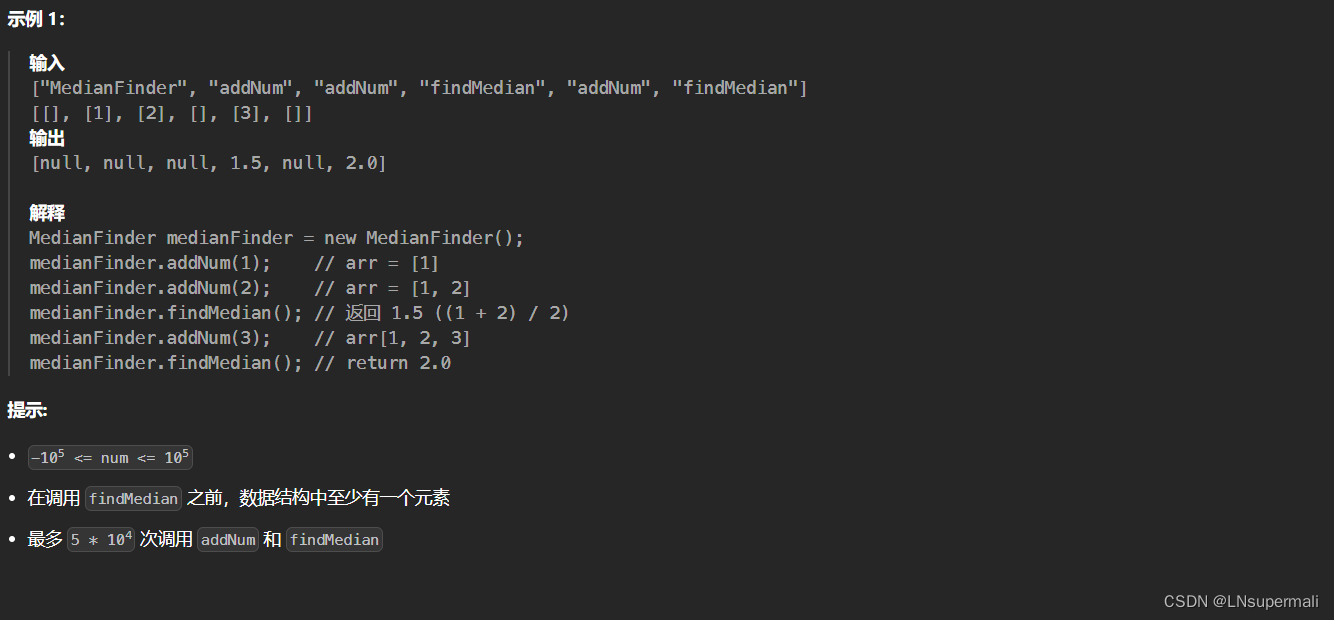
思路

由于该题目的数据是动态的我们可以维护两个堆来解决该问题

1.维护一个大顶堆，一个小顶堆
2.每个堆中元素个数接近n/2；如果n是偶数，两个堆中的数据个数都是n/2;如果n是奇数，则大顶堆中有n/2 + 1个数据，小顶堆中有n/2个数据
3.大顶堆中的数据值都要小于小顶堆中的数据值

即大顶堆中的堆顶元素就是中位数

解题方法

1.（创建堆）按思路创建一个大顶堆和小顶堆
2.（维护堆）：

2.1.如果新插入数据小于等于大顶堆，则将其插入到大顶堆中，否则插入到小顶堆；
2.2.插入数据后，两个堆中的数据量个数不满足思路中的要求2，则我们需要从一个堆中不停的将堆顶元素移动到另一个堆

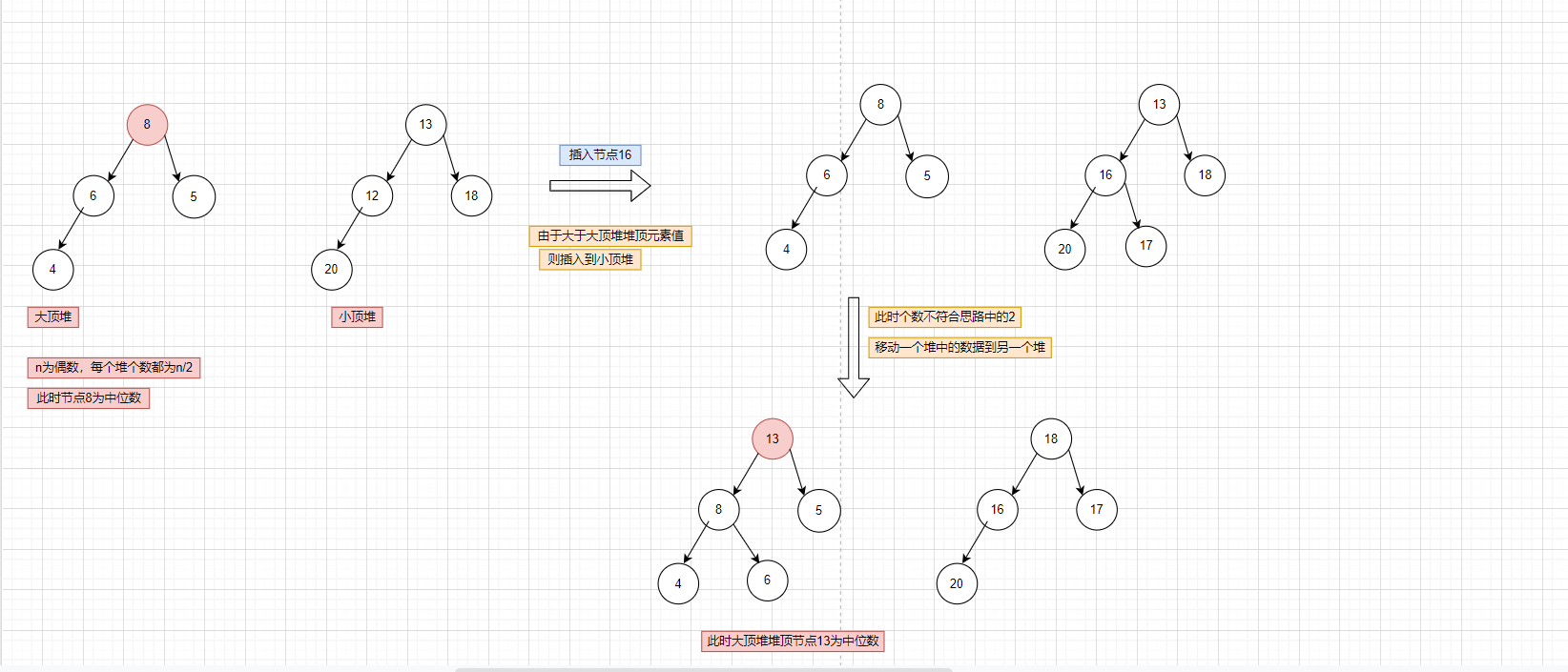
复杂度

时间复杂度:

$addNum:O(logn)$
$findMedian:O(1)$

空间复杂度:

$O(n)$

Code

class MedianFinder {
    /*维护一个大顶堆和小顶堆*/
    private PriorityQueue<Integer> minQueue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o1 - o2;
        }
    });
    private PriorityQueue<Integer> maxQueue = new PriorityQueue<>(new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            return o2 - o1;
        }
    });

    public MedianFinder() {

    }

    /**
     * 数据流插入数据
     *
     * @param num 待插入的数据
     */
    public void addNum(int num) {
        //如果插入数据小于等于大顶堆堆顶元素，大顶堆直接插入
        if (maxQueue.isEmpty() || num <= maxQueue.peek()) {
            maxQueue.add(num);
        } else {
            minQueue.add(num);
        }
        //大顶堆数据量不能小于小顶堆
        while (maxQueue.size() < minQueue.size()) {
            Integer minQueueElement = minQueue.poll();
            maxQueue.add(minQueueElement);
        }
        //小顶堆数据量可以比大顶堆小一个
        while (minQueue.size() < maxQueue.size() - 1) {
            Integer maxQueueElement = maxQueue.poll();
            minQueue.add(maxQueueElement);
        }
    }

    /**
     * 找出中位数
     *
     * @return double
     */
    public double findMedian() {
        //如果大顶堆数据量大于小顶堆
        if (maxQueue.size() > minQueue.size()) {
            return maxQueue.peek();
        } else {
            return (maxQueue.peek() + minQueue.peek()) / 2f;
        }
    }
}


/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */