给大家强调一点，如果这门课你只是通过了，但是其实你并不懂其中的原理，千万不要害怕，不要胆怯，因为后面你还有很多很多的时间来回头巩固它，正所谓“君子报仇，十年不晚”。同样的道理，面临期末考试的时候，需要复习的知识点很多，需要做的题很多，自己记了很多知识点又不会用，很焦虑很着急，而我想说的是，没必要感到焦虑，针对你认为有价值的科目，一步一步慢慢来，把基础打好，后面都不是问题。我个人的做法一直都是，稳扎稳打把基础打好，即使到了最后还有很多内容没有复习到，但是只要考试时，把会写的写上去，不会写的把自己记得的定义一股脑默写上去，实在不行把题目抄一遍，能通过就可以。毕竟来日方长，后面还有时间可以补。最重要的事情是，千万不要熬夜，更不要通宵！！！睡一觉醒来，问题都能过去的。

我们来看第14个函数，int howManyBits(int x)，为了用二进制补码形式表示x，最少需要多少位。比如为了表示12，1100B，引入符号位作为最高位，一共需要5位，即howManyBits(12) = 5； 为了表示298，1 0010 1010B，引入符号位作为最高位，一共需要10位，即howManyBits(298) = 10；为了表示-5，1...1011B，截取从左到右连续的的最后一个1及其后续比特，得到1011B，一共需要4位，即howManyBits(-5) = 4；为了表示0，0B，虽然似乎也需要引入符号位最为最高位，但事实上，可以只用0B，就可以表示1（现在不要深究这一点）；为了表示-1，1...1111B，截取从左到右连续的的最后一个1及其后续比特，得到1B，一共需要1位，即howManyBits(-1) = 1；为了表示0x80000000，截取从左到右连续的的最后一个1及其后续比特，得到0x80000000，一共需要32位，即howManyBits(0x80000000) = 32。在这里，我们隐隐约约就感觉到，对于任意x，只需截取从左到右连续的与第一个比特位相同的最后一个比特及其后续比特，并统计截取到的比特长度就可以，换言之，对于正数x，因为第一个比特位为0，故只需截取从左到右连续的的最后一个0及其后续比特，并统计截取的比特长度；对于负数x，因为第一个比特位为1，故只需截取从左到右连续的的最后一个1及其后续比特，并统计截取的比特长度。下面我们针对x是正或负的两种不同情况，展开分别讨论：第一种情况，x是正，则可以通过如（图1：第14个函数——针对x为正时的思路）中所示的代码得到掩码，进而掩码的比特位数加上1（额外的一个符号位），即为最终需要返回的结果。那么我们该如何统计掩码的比特位数呢？借鉴我们已经写出来的bitCount函数，如（图2：第14个函数——借鉴已经写出来的bitCount函数）所示，得到了如（图3：第14个函数——针对x为正时，统计需要用二进制补码形式表示所需的最小比特长度）所示的代码。

**************************************************************************************************************

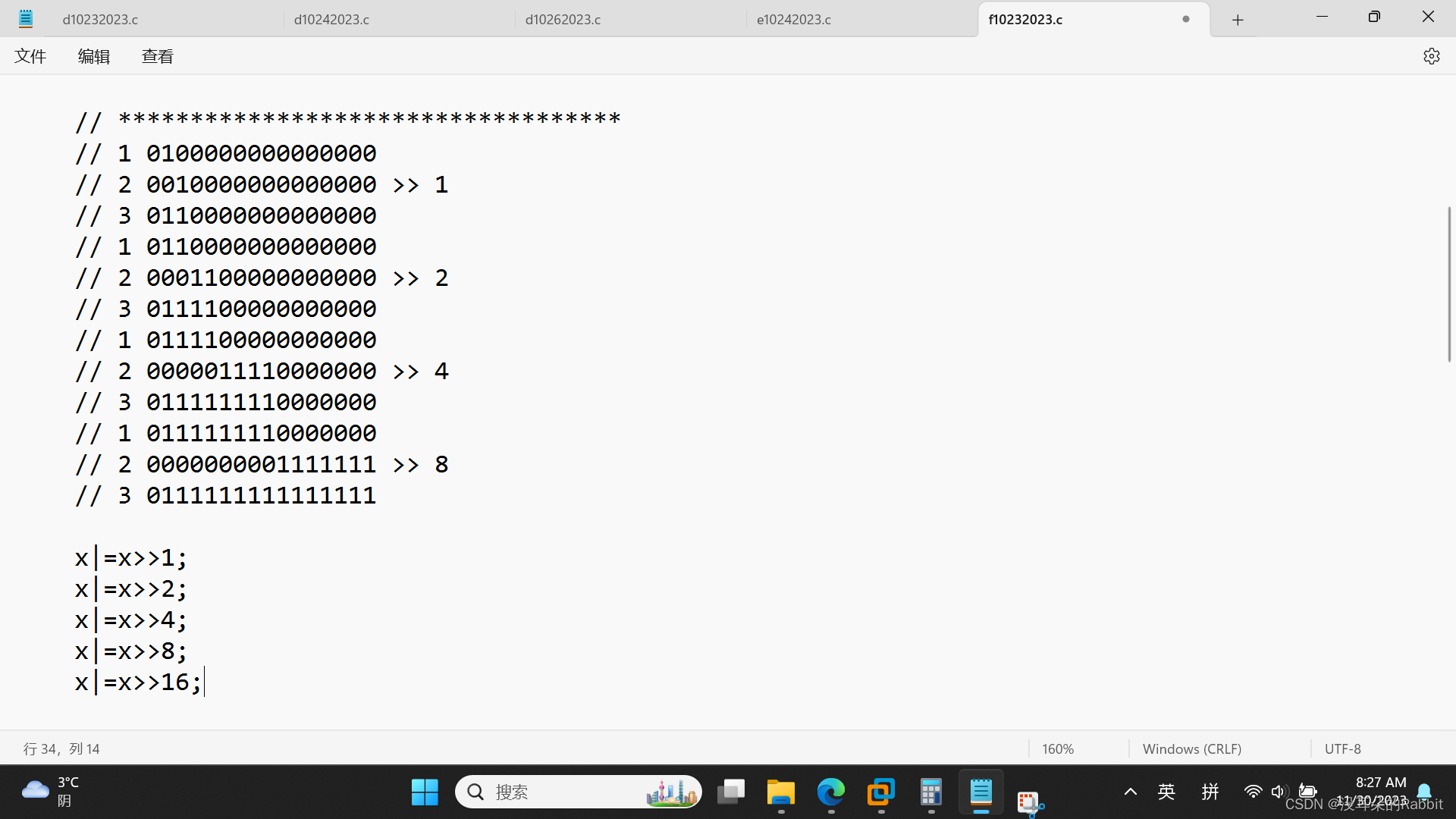
（图1：第14个函数——针对x为正时的思路）

**************************************************************************************************************

**************************************************************************************************************

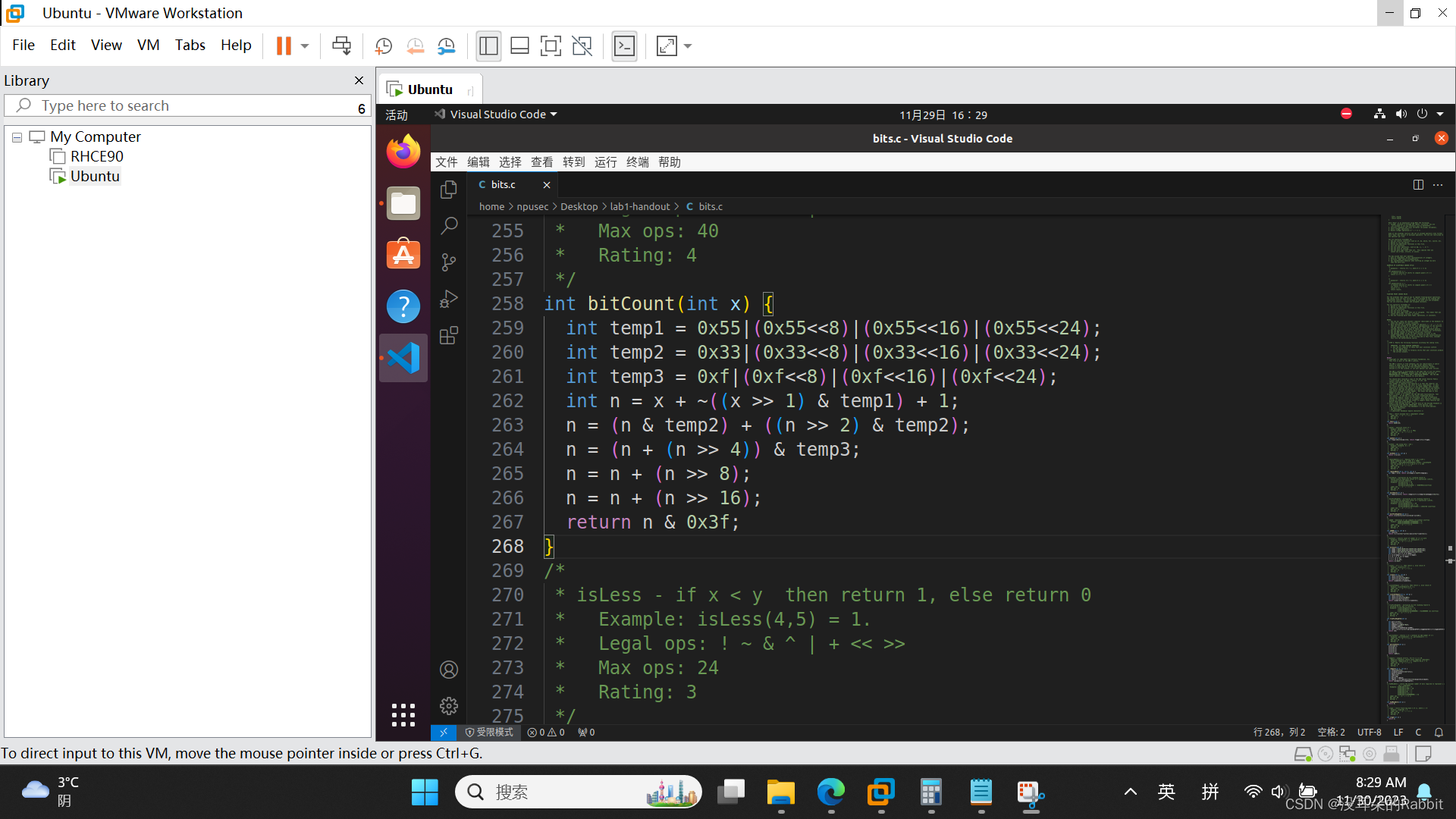
（图2：第14个函数——借鉴已经写出来的bitCount函数）

**************************************************************************************************************

**************************************************************************************************************

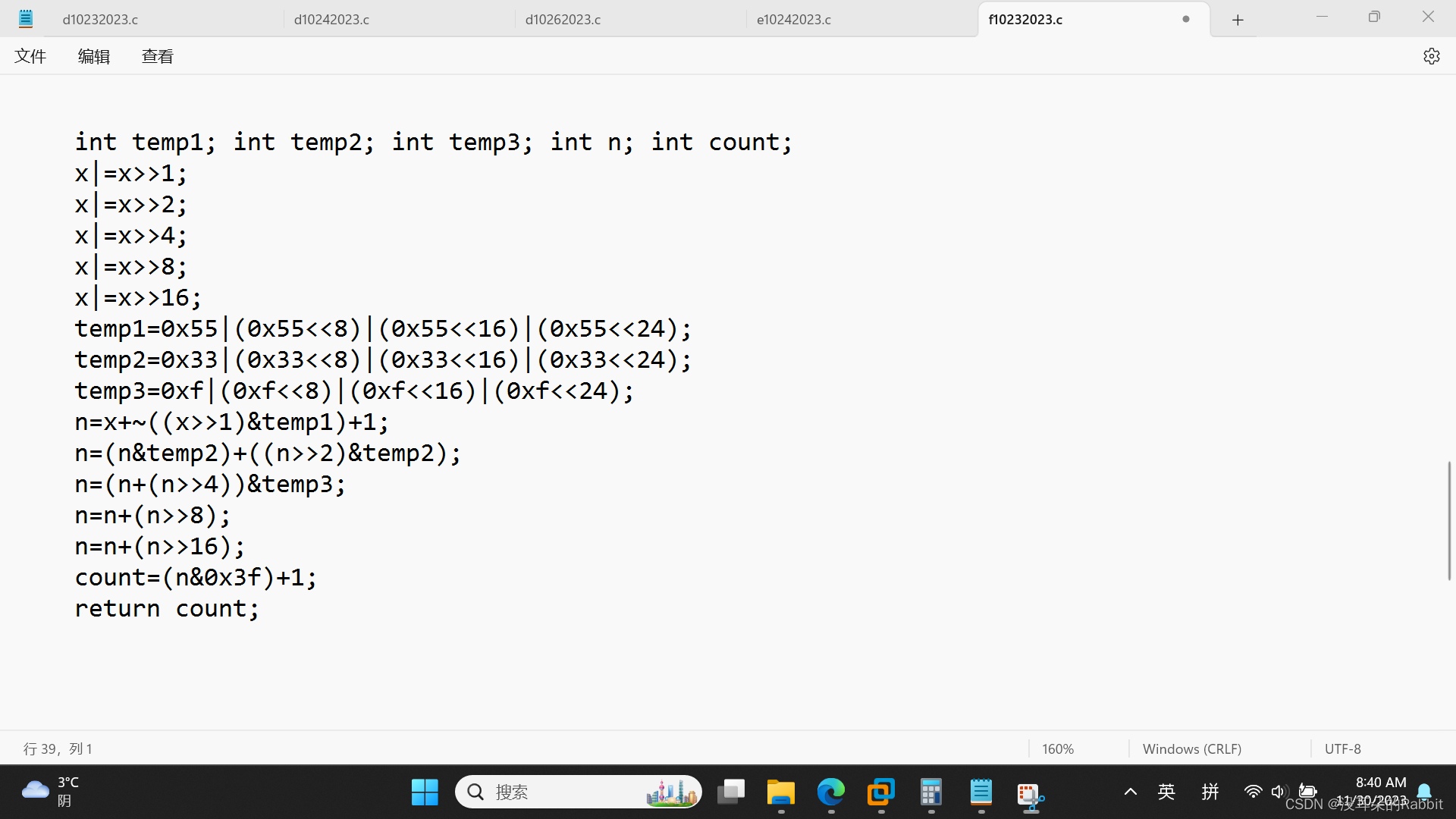
（图3：第14个函数——针对x为正时，统计需要用二进制补码形式表示所需的最小比特长度）

 **************************************************************************************************************

针对第二种情况，如果x为负，那么该怎么办呢？很简单，对其各位取反就可以， 比如0xFFFFFFFF，各位取反得到了0x0，将0x0经过如图1所示的取掩码操作，得到了0x0，接着经过图2中统计字节中1的个数的做法，（如果搞明白了bitCount函数所使用的汉明重量这个知识点，使用的操作符的数量还可以更少，但是考虑到时间紧迫，不得不放弃优化）得到了0，最后根据图3，返回值再加1，得到了1，正好是我们想要的结果howManyBits(-1) = 1；再比如0xFFFF8123，各位取反得到了0x00007EDC,取掩码得到了0x7FFF，统计1的个数为15，最后加1为16，正好是我们期望的结果。那么该如何表示这个条件判断呢？（int sign=x>>31; if(sign) {x=~x} else x）我们可以写作：x=(sign&(~x))|((~sign)&x);。最终，我们仿照前13个函数的检验过程，如（图4：第14个函数）所示。

**************************************************************************************************************

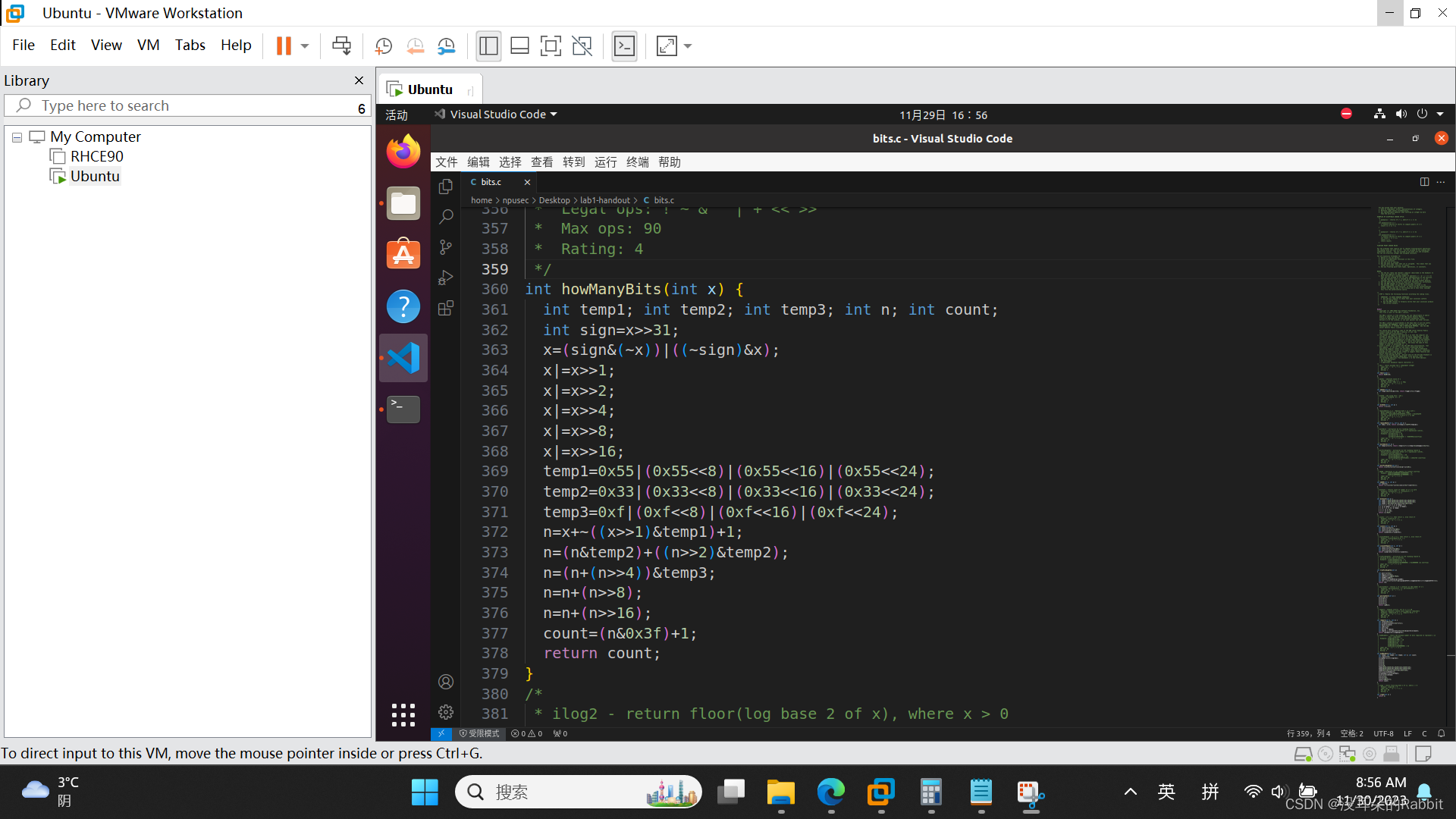
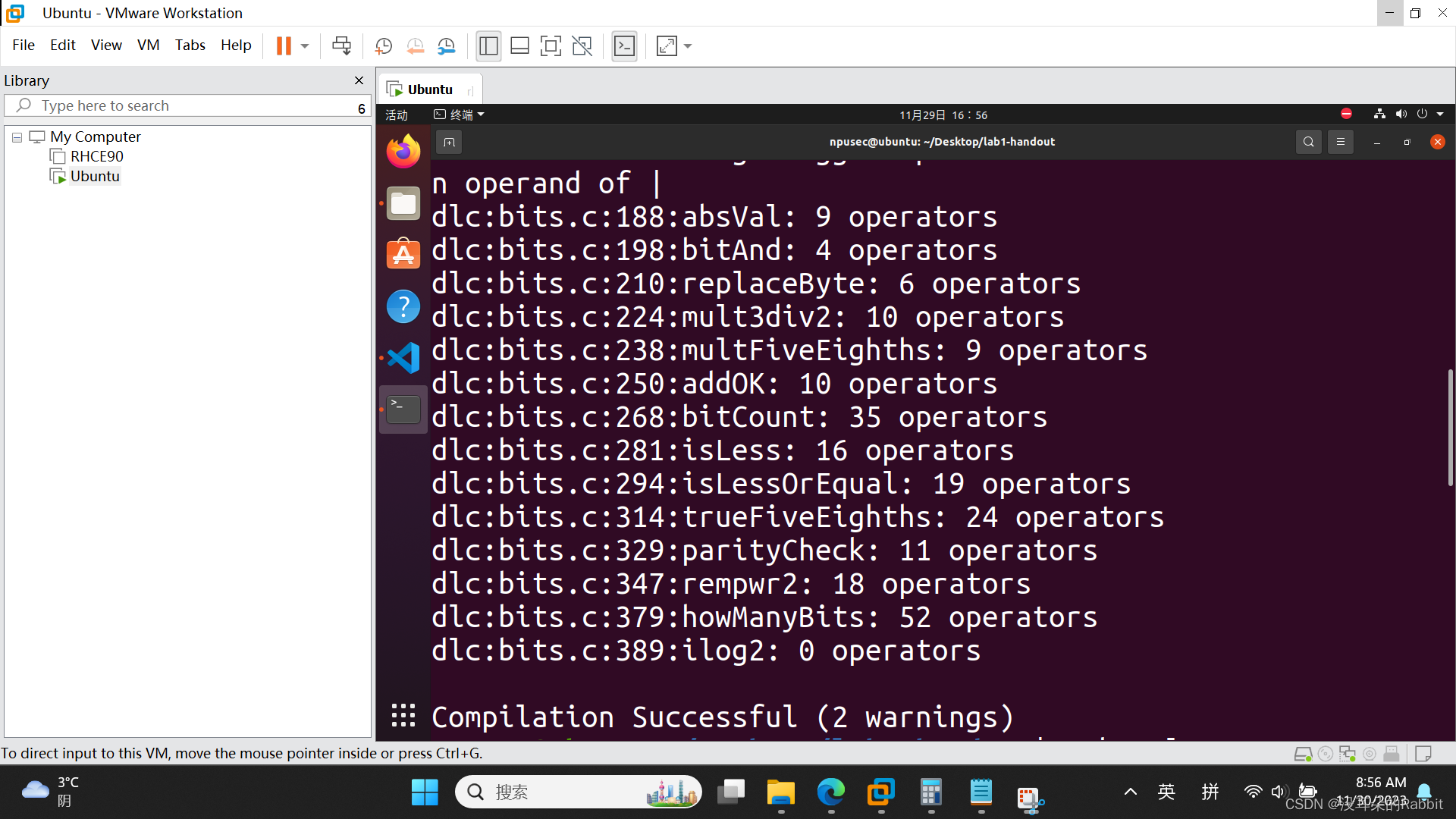
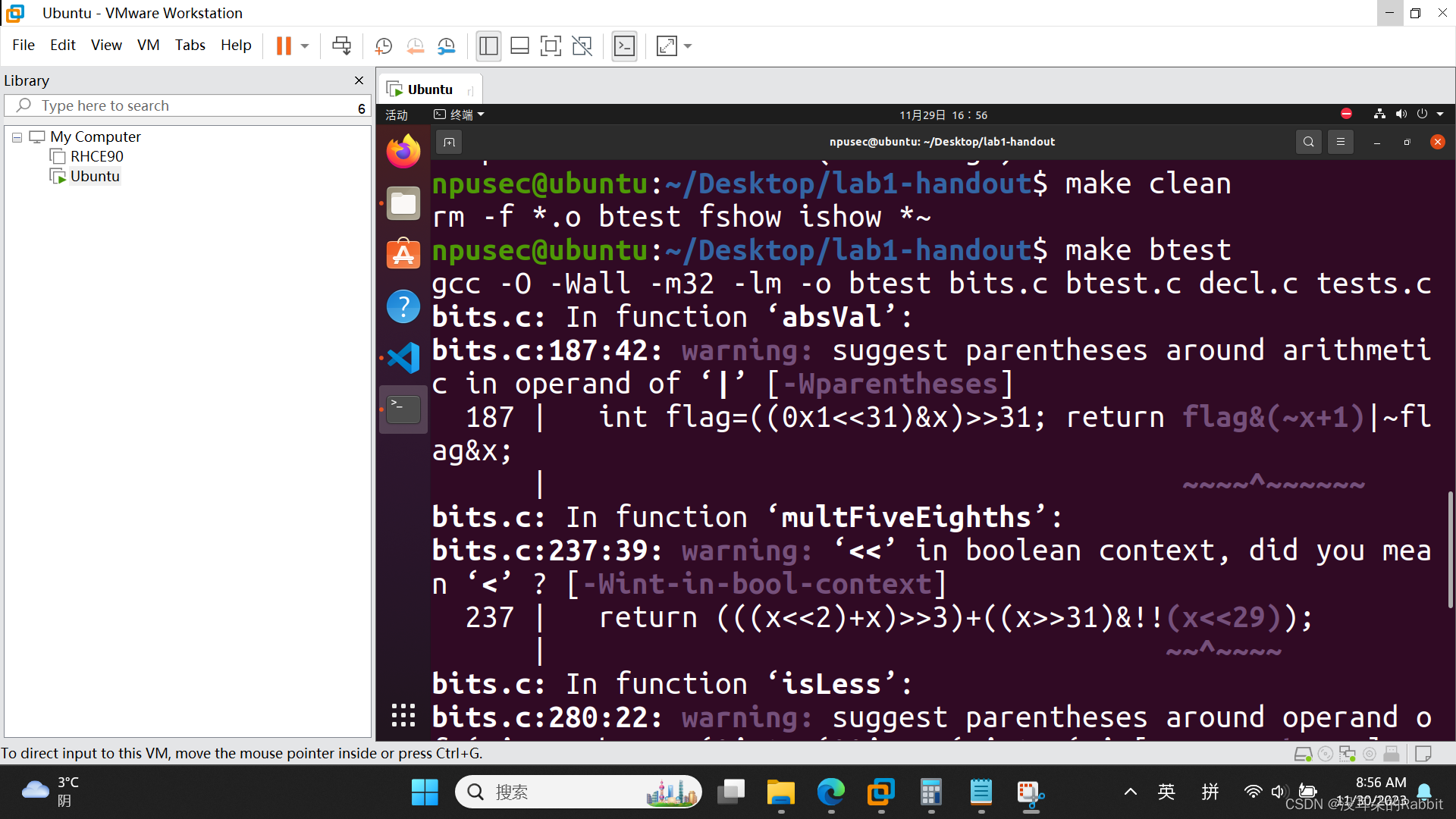
（图4：第14个函数）

**************************************************************************************************************

最后，看第15个函数，int ilog2(int x)，计算log2(x)。按照容易理解的方式，先写出来几个例子：当x=16时，0x10，发现从左到右第一个1的位置是从右到左第5个比特；当x=13时，0xD，发现从左到右第一个1的位置是从右到左第5个比特；当x=255时，0xFF，发现从左到右第一个1的位置是从右到左第8个比特。所以我们的思路便是，得到x的掩码（这个表述不太对，但大概意思是，对于16，得到0x1F，对于13，得到0xF，对于254，得到0xFF），这可以通过图1中的代码实现。接着统计x的掩码中比特位为1的个数，这可以通过之前写过的bitCount函数实现，最终得到的结果减去1，即为我们期望中的答案。我们的代码如（图5：第15个函数——代码）所示。最后仿照前14个函数的检验方法，验证我们的答案是否正确，如（图6：第15个函数）所示。

**************************************************************************************************************

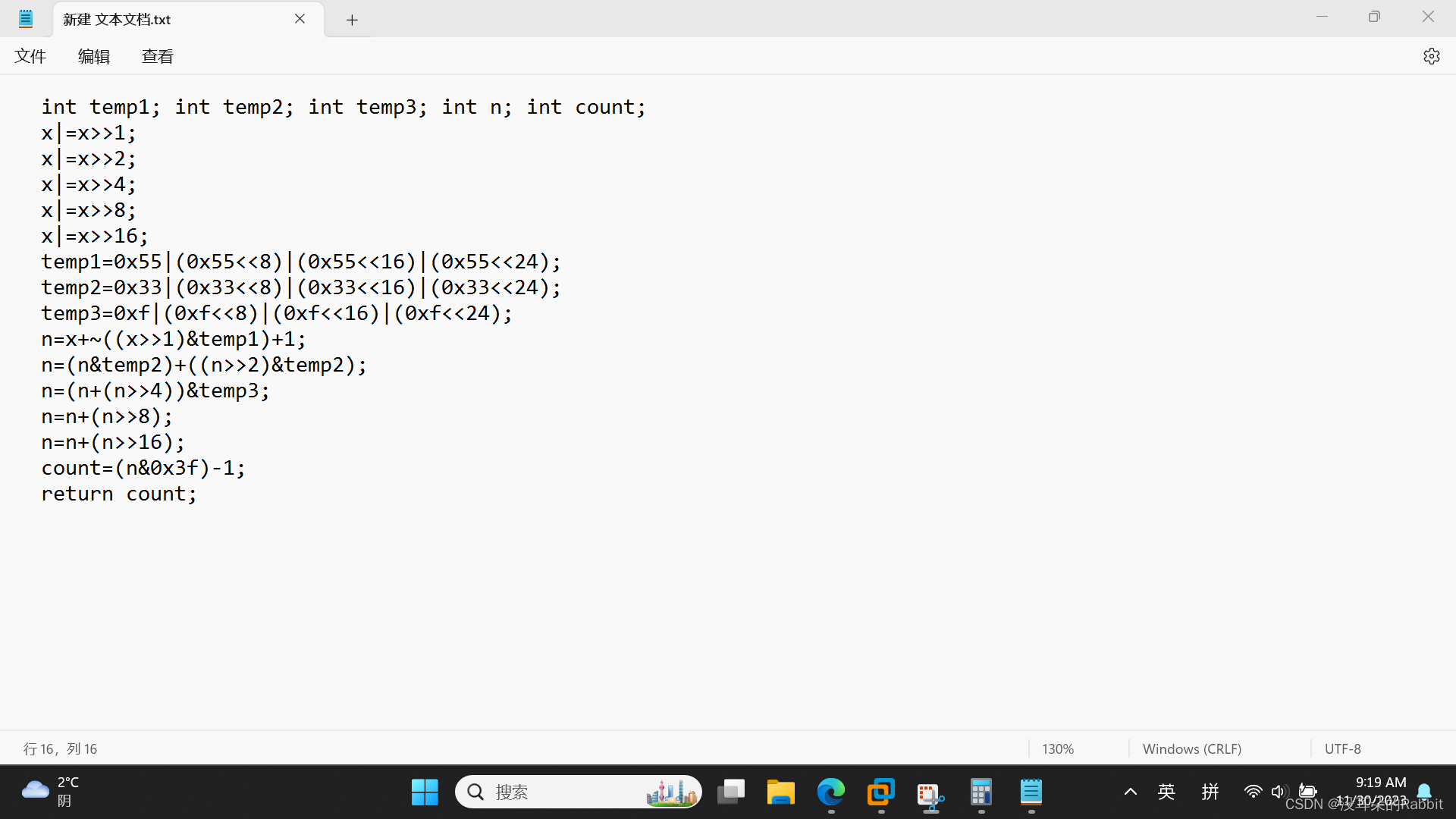
（图5：第15个函数——代码）

**************************************************************************************************************

**************************************************************************************************************

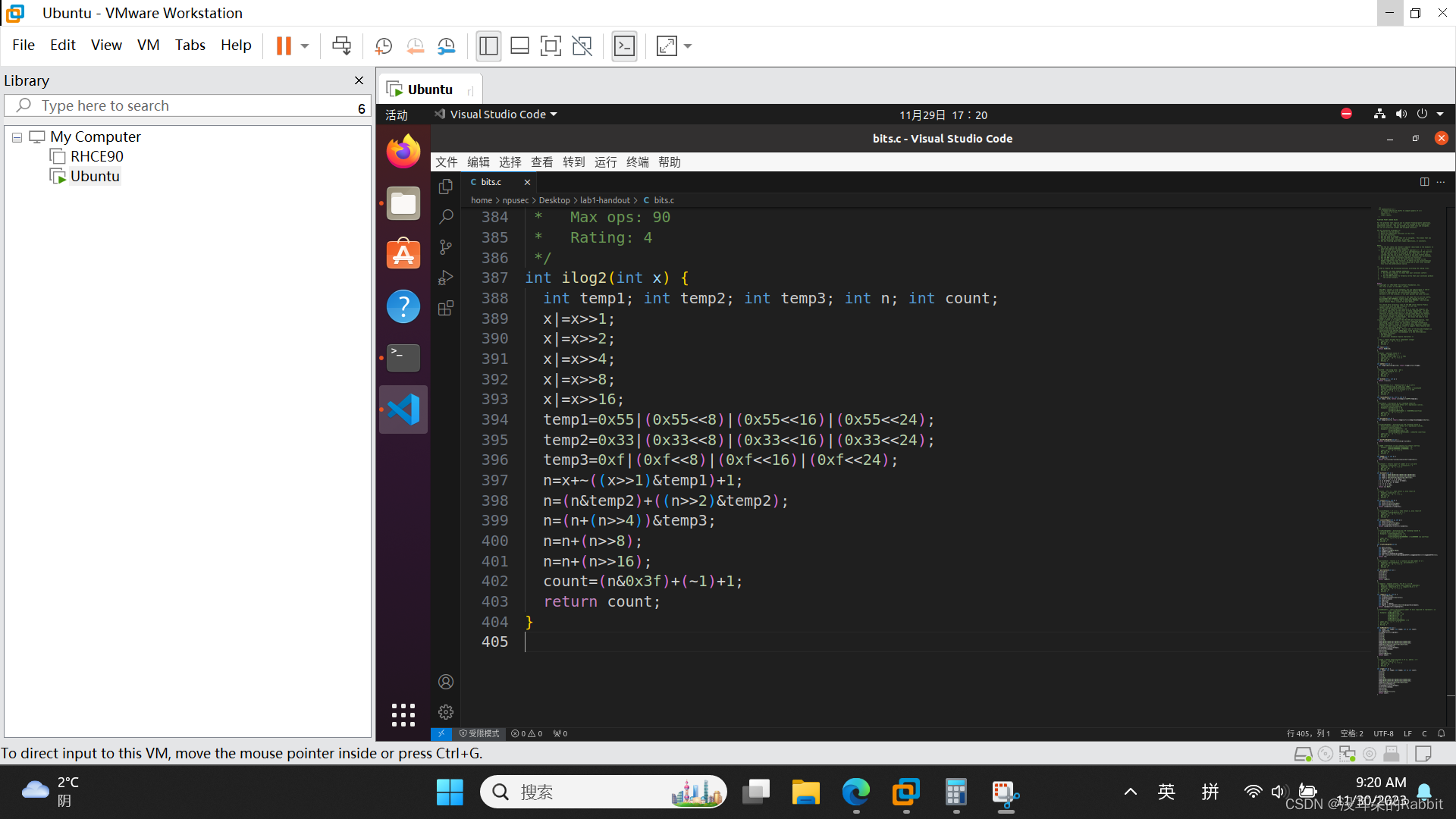
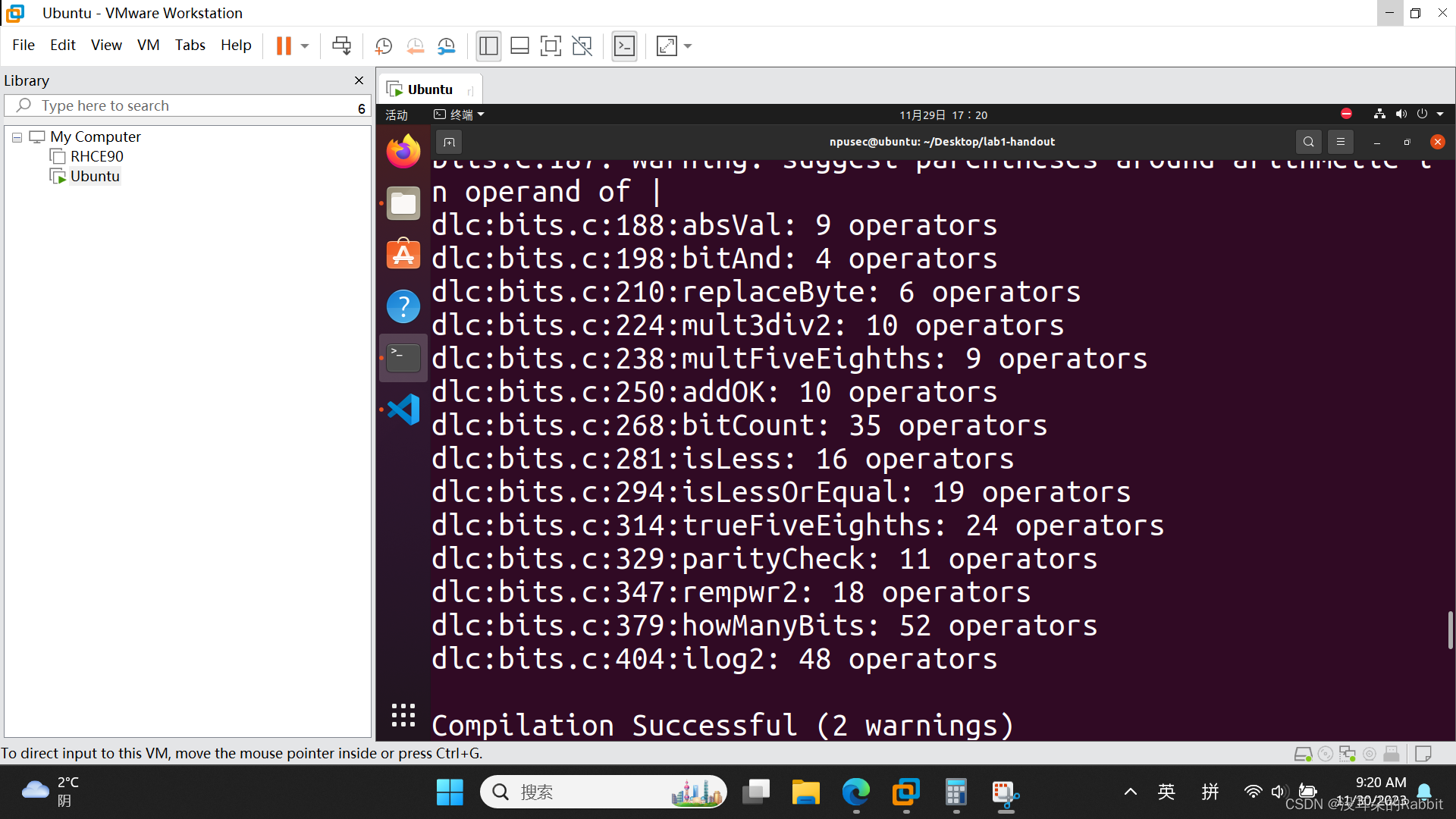
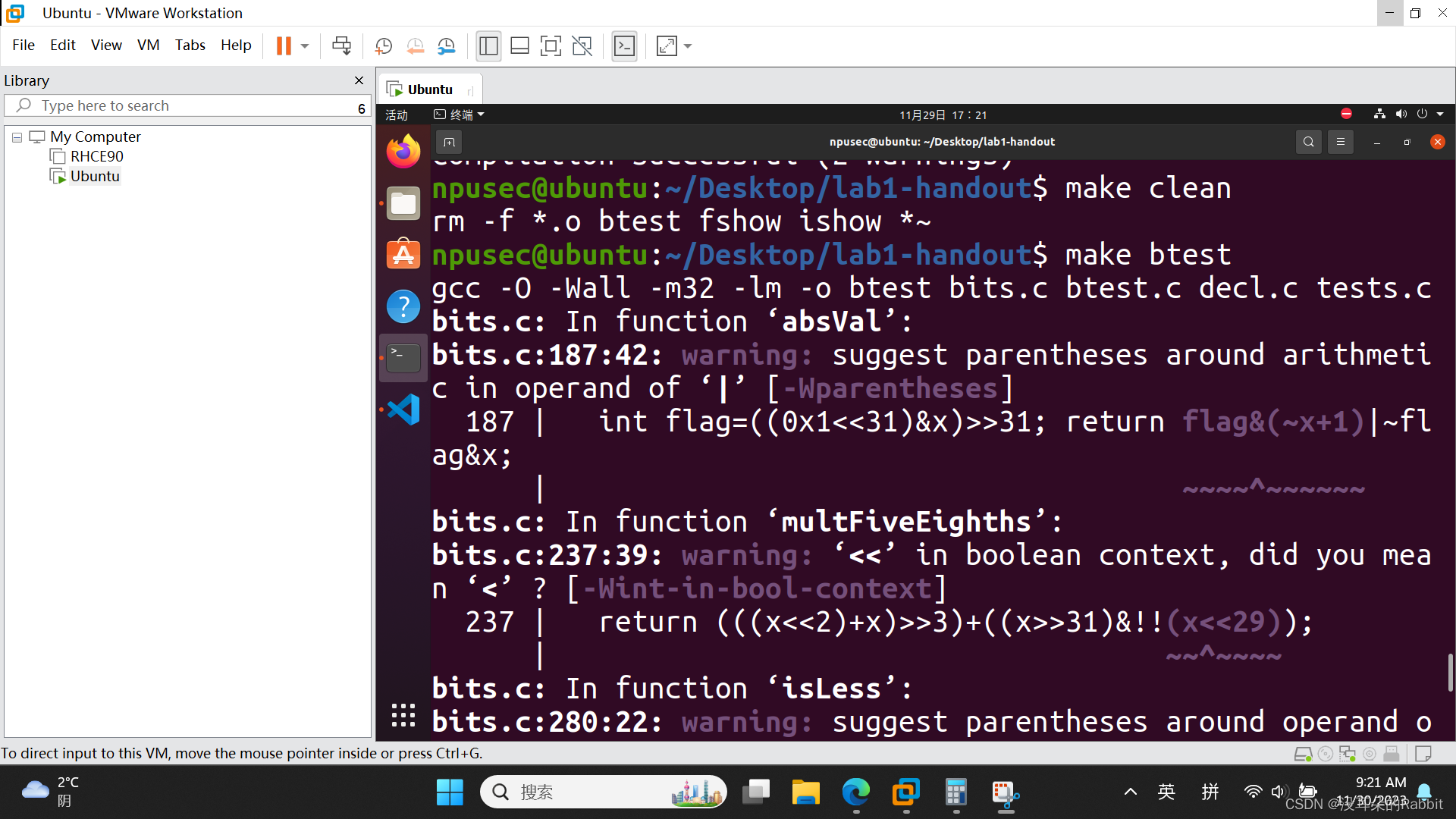
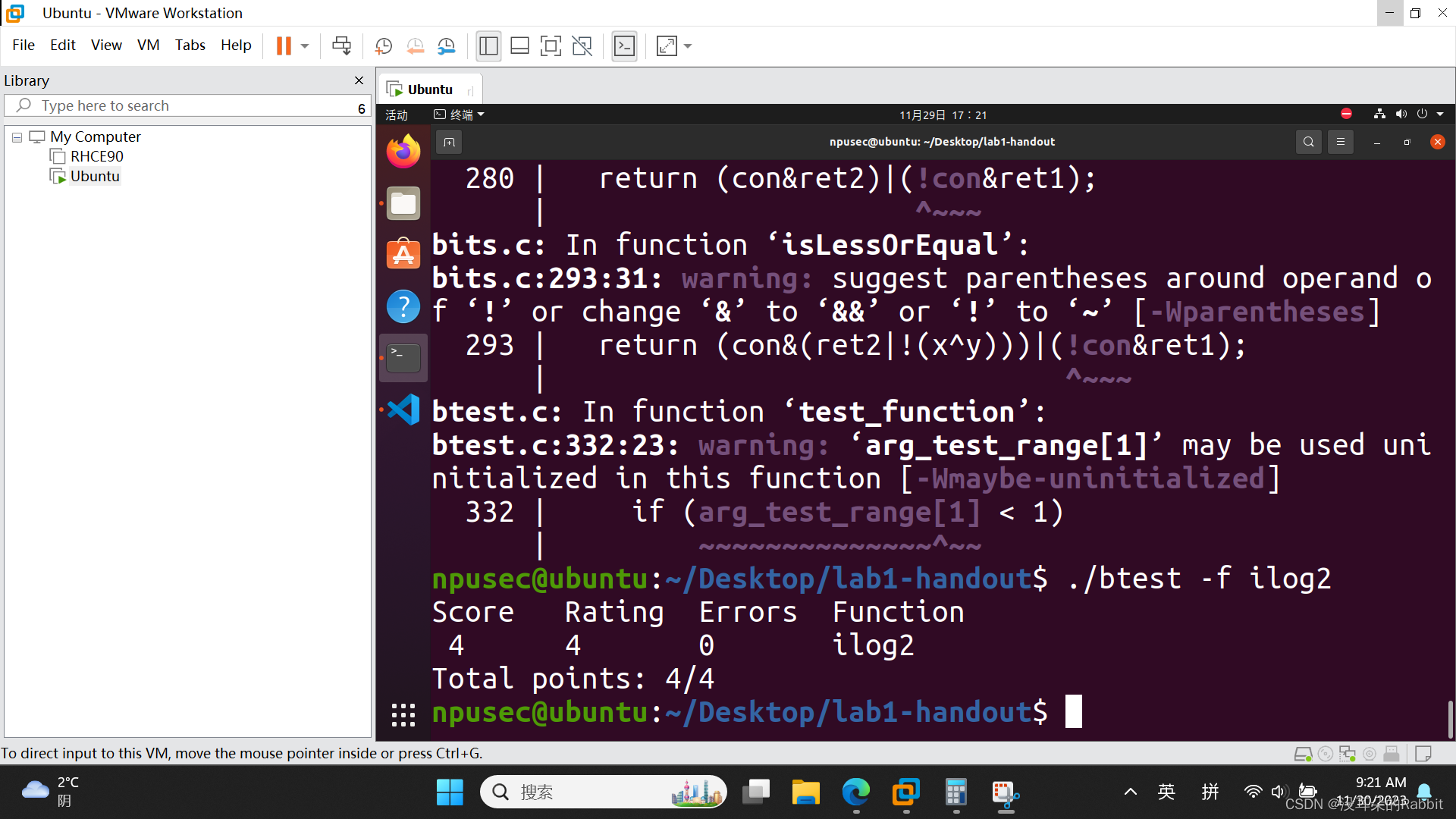
（图6：第15个函数） 

**************************************************************************************************************

最后，这两个函数的源代码如（图7：第14、15个函数的源代码）所示。

 **************************************************************************************************************

int howManyBits(int x) {
  int temp1; int temp2; int temp3; int n; int count;
  int sign=x>>31;
  x=(sign&(~x))|((~sign)&x);
  x|=x>>1;
  x|=x>>2;
  x|=x>>4;
  x|=x>>8;
  x|=x>>16;
  temp1=0x55|(0x55<<8)|(0x55<<16)|(0x55<<24);
  temp2=0x33|(0x33<<8)|(0x33<<16)|(0x33<<24);
  temp3=0xf|(0xf<<8)|(0xf<<16)|(0xf<<24);
  n=x+~((x>>1)&temp1)+1;
  n=(n&temp2)+((n>>2)&temp2);
  n=(n+(n>>4))&temp3;
  n=n+(n>>8);
  n=n+(n>>16);
  count=(n&0x3f)+1;
  return count;
}
int ilog2(int x) {
  int temp1; int temp2; int temp3; int n; int count;
  x|=x>>1;
  x|=x>>2;
  x|=x>>4;
  x|=x>>8;
  x|=x>>16;
  temp1=0x55|(0x55<<8)|(0x55<<16)|(0x55<<24);
  temp2=0x33|(0x33<<8)|(0x33<<16)|(0x33<<24);
  temp3=0xf|(0xf<<8)|(0xf<<16)|(0xf<<24);
  n=x+~((x>>1)&temp1)+1;
  n=(n&temp2)+((n>>2)&temp2);
  n=(n+(n>>4))&temp3;
  n=n+(n>>8);
  n=n+(n>>16);
  count=(n&0x3f)+(~1)+1;
  return count;
}

（图7：第14、15个函数的源代码）

**************************************************************************************************************