首先,我想吐槽一下,看了好几篇聚焦评价函数的文章,说到底都是一篇文章转载或者重复上传,介绍了将近 15 种清晰度的算法,原文找了半天都没找到在哪,最多也仅能找到一些比较早的转载。
- 无参考图像的清晰度评价方法
- 模糊图像检测-无参考图像的清晰度评价
里面有些比较有名的算法,如 Brenner,Tenengrad,Laplacian,Variance,Vollath, Entropy 这些都没啥好说的,本文后面也会给出相应的公式,但是这些文章都混进去了一些奇怪的东西,例如 SMD 和 SMD2 函数 。然后 Reblur,查了半天也是没有找到任何有用的信息,直接放弃了。
关于 “SMD 与 SMD2” 的一些溯源
而且有些离谱的东西,例如里面的 SMD 灰分方差函数,我特么 baidu, bing,google 了一遍,除了这篇文章的徒子徒孙,没找到别的有用的信息,最开始的出处都没找到了,连这个缩写是哪几个单词的缩写都没搞明白。最终在参考文献里找到一篇国人的文章:一种快速高灵敏度聚焦函数

终于看到上面这个,出现在很多文章里的公式,然后顺藤摸瓜,找到引用 [1] 的文章:光学显微镜自动聚焦算法研究,Ctrl F 找一下 SMD,发现文章中关键字零匹配。
合着你这是自己给别人编了个名字?
然后继续读这篇文章,感觉终于接近真相了,这个梯度计算的公式在这文章里是为了快速选择聚焦区域的,并不是拿来做聚焦评价函数的。这文章(一种快速高灵敏度聚焦函数)感觉也太水了,就随随便便的一顿编,结果都是引了这篇文章的基本都错了。
当然这个公式不是不能用,毕竟和 Brenner 还有 Squared gradient 本质没啥区别。

然后接着说 SMD2,这个就是这文章(一种快速高灵敏度聚焦函数)提出的改进版本的 SMD,呃。。。

写成公式就是:
F
=
∑
M
∑
N
[
g
(
i
,
j
)
−
g
(
i
+
1
,
j
)
]
[
g
(
i
,
j
)
−
g
(
i
,
j
+
1
)
]
F = \sum_M \sum_N \left [ g(i, j) - g(i+1, j) \right ]\left [ g(i, j) - g(i, j+1) \right ]
F=M∑N∑[g(i,j)−g(i+1,j)][g(i,j)−g(i,j+1)]感觉更像 Brenner 和 Squared gradient,不好评价。
- SMD:光学显微镜自动聚焦算法研究
- SMD2:一种快速高灵敏度聚焦函数
EAV 边缘锐度算法 与 PAV 点锐度算法
徐贵力、张霞等提出了一种基于边缘锐度的算法用于评价图像的清晰度。通过统计图像某一边缘方向的灰度变化情况来评价。
这段话也是每篇文章都有的(毕竟都是拷贝粘贴的)
然后一通寻找,只找了张霞的(中巴地球资源一号卫星多光谱扫描图象质量评价)文章里确实提到了使用 EAV 算法来评价清晰度,但是不知道是不是源头。徐贵力的那篇论文我没有找到。
但是我这里也有一个问题,EAV 明显是指 Edge Acutance Value,边缘锐度值的意思,为啥介绍的都是经过王鸿南改进的点锐度算法,还是使用 EAV 来作为缩写,不应该根据 Point Acutance Value 缩写城 PAV 吗?迷惑。
论文里的公式如下: E A V = 1 ∣ f ( b ) − f ( a ) ∣ ∑ a b ( d f / d x ) 2 EAV = \frac{1}{|f(b)-f(a)|}\sum_a^b(\mathrm{d}f / \mathrm{d}x ) ^2 EAV=∣f(b)−f(a)∣1a∑b(df/dx)2 这么看这个公式,确实迷惑。
其中:df/dx为边缘法向的灰度变化率,f(b) - f(a)为该方向的总体灰度变化。该算法只对图像的特定边缘区域做统计,能否代表整幅图像的清晰度仍有疑问,此外计算前需人工选定边缘区域,不便实现程序运算的自动化。
这个解释也让我一头雾水,可能是我理解力太差了,大概尝试着去理解,就是 d f / d x \mathrm{d}f / \mathrm{d}x df/dx 就是求梯度,但是一般在图像处理里面,都会使用差分来替代。而 a a a 和 b b b 表示人工选定的边缘的法线方向吧,算是我还是放弃了。这个 EAV 也没办法作为聚焦评价函数,所以也就不管它了。
然后来到 PAV 点锐度算法这里,这个论文中的公式是: P A V = 1 M N ∑ i = 1 M × N ∑ a = 1 8 ∣ d f / d x ∣ PAV = \frac{1}{MN}\sum_{i=1}^{M\times N}\sum _{a=1}^8|\mathrm{d}f /\mathrm{d}x | PAV=MN1i=1∑M×Na=1∑8∣df/dx∣我为了方便理解,方便代码实现,将公式写成了下面的样子: P A V = 1 M N ∑ M − 1 ∑ N − 1 ( a 2 + b 1 ) 2 PAV = \frac{1}{MN}\sum _{M-1}\sum_{N-1}\left ( \frac{a}{\sqrt{2}} + \frac{b}{1} \right )^2 PAV=MN1M−1∑N−1∑(2a+1b)2 a = g ( i − 1 , j − 1 ) + g ( i + 1 , j − 1 ) + g ( i − 1 , j + 1 ) + g ( i + 1 , j + 1 ) − 4 ⋅ g ( i , j ) a = g(i-1, j-1) + g(i+1, j-1) + g(i-1, j+1) + g(i+1, j+1) - 4\cdot g(i, j) a=g(i−1,j−1)+g(i+1,j−1)+g(i−1,j+1)+g(i+1,j+1)−4⋅g(i,j) b = g ( i − 1 , j ) + g ( i + 1 , j ) + g ( i , j + 1 ) + g ( i , j − 1 ) − 4 ⋅ g ( i , j ) b = g(i-1, j) + g(i+1, j) + g(i, j+1) + g(i, j-1) - 4\cdot g(i, j) b=g(i−1,j)+g(i+1,j)+g(i,j+1)+g(i,j−1)−4⋅g(i,j)
和下面的拉普拉斯梯度挺像的,如果借助拉普拉斯算子来理解的话,假设有一个叫做 PAV 的算子,那么它将会是: PAV operator = [ 1 / 2 1 1 / 2 1 − 4 − 2 2 1 1 / 2 1 1 / 2 ] \text{PAV operator} = \begin{bmatrix} 1/\sqrt{2} & 1 & 1/\sqrt{2}\\ 1 & -4-2\sqrt{2} & 1\\ 1/\sqrt{2} & 1 & 1/\sqrt{2} \end{bmatrix} PAV operator= 1/211/21−4−2211/211/2
下面有两个代码实现 PAV 点锐度算法:
- ENVIIDL:利用ENVIIDL实现图像清晰度评价——点锐度算法
- C++:EVA改进(点锐度算法)图像清晰度评价方法C++实现
下面是原论文出处:
- EAV:中巴地球资源一号卫星多光谱扫描图象质量评价
- PAV:图像清晰度评价方法研究
NRSS 和 Reblur
先说 NRSS,也是国人提出来的,看了一下论文,无关的东西就不说了,直接说和清晰度评价指标相关的。
图像清晰与否,本质是包含高频信息的多少,梯度平方和,能量熵函数之类的,都是通过计算高频分量的多少来评价图像是否清晰,也就是说:图像的高频信息越多,则图像越清晰。
这篇论文(一种针对图像模糊的无参质量评价指标)就提出了一种评价高频分量多少的方法: NRSS。
步骤就是先进行低通滤波,得到一幅参考图像,然后计算参考图像和原图的结构相似度。因为低通滤波只是将高的部分过滤了,还保留了低频部分,如果图像高频部分多(清晰的图像),得到的参考图像就会损失很多高频成分,计算两者结构相似度(这里使用 SSIM 计算)的时候得到的数值就会比较小。
就是说,参考图像(经过低通滤波的)和原图的 SSIM 值越小,表示原图越清晰。
公式: N R S S = 1 − 1 N ∑ n = 1 N S S I M ( i n , j n ) NRSS = 1 - \frac{1}{N} \sum _{n=1}^N SSIM(i_n, j_n) NRSS=1−N1n=1∑NSSIM(in,jn)其中, N N N 表示图像中梯度信息最丰富的 N N N 个图像块,原文是针对全图进行的清晰度分析,如果是要在聚焦的时候对焦点的某个区域进行分析的话,就只需要 N = 1 N=1 N=1 一个图像块就行了,这个公式也可以简单写成: N R S S = 1 − S S I M ( i , j ) NRSS = 1 - SSIM(i, j) NRSS=1−SSIM(i,j) 只需要对焦点区域进行 NRSS 就行了。
因为也涉及到 SSIM,就简单的介绍一下,公式是: l ( x , y ) = 2 μ x μ y + C 1 μ x 2 + μ y 2 + C 1 , c ( x , y ) = 2 σ x σ y + C 2 σ x 2 + σ y 2 + C 2 , s ( x , y ) = σ x y + C 3 σ x σ y + C 3 l(x, y) = \frac{2\mu_x\mu_y + C_1}{\mu_x^2 + \mu_y^2 + C_1}, \space \space \space \space \space c(x, y) = \frac{2\sigma _x\sigma_y + C_2}{\sigma_x^2 + \sigma_y^2 + C_2}, \space \space \space \space \space s(x, y) = \frac{\sigma _{xy} + C_3}{\sigma _x\sigma _y + C_3} l(x,y)=μx2+μy2+C12μxμy+C1, c(x,y)=σx2+σy2+C22σxσy+C2, s(x,y)=σxσy+C3σxy+C3 其中 l ( x , y ) l(x, y) l(x,y) 是亮度比较, c ( x , y ) c(x, y) c(x,y) 是对比度比较, s ( x , y ) s(x, y) s(x,y) 是结构信息比较,然后整合起来: S S I M ( x , y ) = [ l ( x , y ) ] α [ c ( x , y ) ] β [ ( s ( x , y ) ) ] γ SSIM(x, y) = [l(x, y)]^\alpha [c(x, y)]^\beta[(s(x,y))]^\gamma SSIM(x,y)=[l(x,y)]α[c(x,y)]β[(s(x,y))]γ具体就不多涉及了,可以看看参考文章。
然后看到这里,然后看看这篇文章(无参考图像的清晰度评价方法)里提到的 Reblur 的结构,是不是感觉很熟悉,不就是一个意思吗,就是使用低通滤波得到一个模糊的参考图像,然后和原图进行结构相似度的比较,得到一个评价指标。得亏那片文章还煞有介事得整出一个 Reblur 来。
- NRSS:一种针对图像模糊的无参质量评价指标
使用比较普遍的一些算法
基于自相关
Vollath’s F4
F = ∑ M − 1 ∑ N g ( i + 1 , j ) ⋅ g ( i , j ) − ∑ M − 2 ∑ N g ( i + 2 , j ) ⋅ g ( i , j ) F = \sum_{M-1}\sum_N g(i+1, j)\cdot g(i, j) - \sum_{M-2}\sum_N g(i+2, j) \cdot g(i,j) F=M−1∑N∑g(i+1,j)⋅g(i,j)−M−2∑N∑g(i+2,j)⋅g(i,j)
Vollath’s F5
F = ∑ M − 1 ∑ N g ( i + 1 , j ) ⋅ g ( i , j ) − ( M − 1 ) ⋅ N ⋅ g ˉ F = \sum_{M-1}\sum_N g(i+1, j)\cdot g(i, j) - (M-1)\cdot N\cdot \bar{g} F=M−1∑N∑g(i+1,j)⋅g(i,j)−(M−1)⋅N⋅gˉ
基于统计
方差 Variance
F = 1 M N ∑ M ∑ N ∣ g ( i , j ) − g ˉ ∣ F = \frac{1}{MN}\sum_M\sum_N \left | g(i, j) - \bar{g} \right | F=MN1M∑N∑∣g(i,j)−gˉ∣
归一化方差 Normalized Variance
F = 1 M N ⋅ g ˉ ∑ M ∑ N ∣ g ( i , j ) − g ˉ ∣ F = \frac{1}{MN\cdot \bar{g} }\sum_M\sum_N \left | g(i, j) - \bar{g} \right | F=MN⋅gˉ1M∑N∑∣g(i,j)−gˉ∣
基于直方图
熵 Entropy
F = − ∑ l p l ⋅ log 2 p l F = - \sum_{l} p_l \cdot \log_{2} p_l F=−l∑pl⋅log2pl其中 p l p_l pl 是灰度值的相对频率。
log 直方图的方差(Variance of log histogram)
F = ∑ l ( l − E log ( l ) ) 2 ⋅ log p l E log ( l ) = ∑ l l ⋅ log p l F = \sum_{l}(l - E_{\text{log}}(l))^2 \cdot \log p_l \\ E_{\log}(l) = \sum_l l \cdot \log p_l F=l∑(l−Elog(l))2⋅logplElog(l)=l∑l⋅logpl
基于图像差分
EOG(Energy of gradient)
F = ∑ M − 1 ∑ N − 1 ( [ g ( i + 1 , j ) − g ( i , j ) ] 2 + [ g ( i , j + 1 ) − g ( i , j ) ] 2 ) F = \sum _{M-1}\sum _{N-1} \left( \left [g(i+1, j) - g(i, j)\right]^2 + \left [g(i, j+1) - g(i, j) \right ]^2 \right ) F=M−1∑N−1∑([g(i+1,j)−g(i,j)]2+[g(i,j+1)−g(i,j)]2)
Robert
F
=
∑
M
−
1
∑
N
−
1
(
[
g
(
i
+
1
,
j
+
1
)
−
g
(
i
,
j
)
]
2
+
[
g
(
i
+
1
,
j
)
−
g
(
i
,
j
+
1
)
]
2
)
F = \sum _{M-1}\sum _{N-1} \left( \left [g(i+1, j+1) - g(i, j)\right]^2 + \left [g(i+1, j) - g(i, j+1) \right ]^2 \right )
F=M−1∑N−1∑([g(i+1,j+1)−g(i,j)]2+[g(i+1,j)−g(i,j+1)]2)
感觉和 EOG 没有什么太大的区别
拉普拉斯能量梯度(Energy of image Laplacian)
F = ∑ M − 1 ∑ N − 1 ( g ( i , j + 1 ) + g ( i , j − 1 ) + g ( i + 1 , j ) + g ( i − 1 , j ) − 4 ⋅ g ( i , j ) ) 2 F = \sum _{M-1}\sum _{N-1}\left ( g(i, j+1) + g(i, j-1) + g(i+1, j) + g(i-1, j) - 4\cdot g(i, j) \right )^2 F=M−1∑N−1∑(g(i,j+1)+g(i,j−1)+g(i+1,j)+g(i−1,j)−4⋅g(i,j))2
相当于与拉普拉斯算子进行了一次卷积运算然后再平方: L = [ 0 1 0 1 − 4 1 0 1 0 ] L = \begin{bmatrix} 0 & 1 & 0\\ 1 & -4 & 1\\ 0 & 1 & 0 \end{bmatrix} L= 0101−41010
Tenengrad gradient
F = ∑ M ∑ N ( G x 2 ( i , j ) + G y 2 ( i , j ) ) F = \sum_M\sum _N \left ( G_x^2(i, j) + G_y^2(i, j) \right ) F=M∑N∑(Gx2(i,j)+Gy2(i,j))其中 G x G_x Gx 和 G y G_y Gy 是与 Sobel 算子的卷积。
Brenner gradient
F = ∑ M ∑ N − 2 ∣ g ( i , j + 2 ) − g ( i , j ) ∣ 2 while ∣ g ( i , j + 1 ) − g ( i , j ) ∣ ≥ θ F = \sum_M\sum _{N-2} \left | g(i, j+2) - g(i, j) \right |^2 \space \space \space \space \text{while} \space \space \left | g(i, j+1) - g(i, j) \right | \ge \theta F=M∑N−2∑∣g(i,j+2)−g(i,j)∣2 while ∣g(i,j+1)−g(i,j)∣≥θ
一阶高斯导数(First-order Gaussian derivative)
F = 1 M N ∑ M ∑ N ( ( g ( i , j ) ⋅ G x ( x , y , σ ) ) 2 + ( g ( i , j ) ⋅ G y ( x , y , σ ) ) 2 ) F = \frac{1}{MN}\sum _M\sum _N \left( \left ( g(i, j)\cdot G_x(x, y, \sigma ) \right ) ^2 + \left ( g(i, j)\cdot G_y(x, y, \sigma ) \right ) ^2 \right ) F=MN1M∑N∑((g(i,j)⋅Gx(x,y,σ))2+(g(i,j)⋅Gy(x,y,σ))2)其中 G x ( x , y , σ ) G_x(x, y, \sigma) Gx(x,y,σ) 和 G y ( x , y , σ ) G_y(x, y, \sigma) Gy(x,y,σ) 是一阶高斯导数,且标准差为 σ = 3 2 d \sigma=\frac{\sqrt{3}}{2}d σ=23d
Squared gradient
F = ∑ M ∑ N − 1 ∣ g ( i , j + 1 ) − g ( i , j ) ∣ 2 while ∣ g ( i , j + 1 ) − g ( i , j ) ∣ ≥ θ F = \sum_M\sum _{N-1} \left | g(i, j+1) - g(i, j) \right |^2 \space \space \space \space \text{while} \space \space \left | g(i, j+1) - g(i, j) \right | \ge \theta F=M∑N−1∑∣g(i,j+1)−g(i,j)∣2 while ∣g(i,j+1)−g(i,j)∣≥θ几乎和 Brenner gradient 一样,就是相邻像素选择不同。
Threshold absolute gradient
F = ∑ M ∑ N − 1 ∣ g ( i , j + 1 ) − g ( i , j ) ∣ while ∣ g ( i , j + 1 ) − g ( i , j ) ∣ ≥ θ F = \sum_{M}\sum _{N-1} \left | g(i, j+1) - g(i, j) \right | \space \space \space \space \text{while} \space \space \left | g(i, j+1) - g(i, j) \right | \ge \theta F=M∑N−1∑∣g(i,j+1)−g(i,j)∣ while ∣g(i,j+1)−g(i,j)∣≥θ
Absolute Tenengrad
F = ∑ M ∑ N ( ∣ G x ( i , j ) ∣ + ∣ G y ( i , j ) ∣ ) F = \sum _M\sum _N \left ( |G_x(i, j)| + |G_y(i, j)|\right ) F=M∑N∑(∣Gx(i,j)∣+∣Gy(i,j)∣) 其中 G x G_x Gx 和 G y G_y Gy 是与 Sobel 算子的卷积。
基于峰值和谷值的深度
image power
F = ∑ M ∑ N g ( i , j ) 2 while g ( i , j ) ≥ θ F = \sum _M \sum _N g(i, j)^2 \space \space \space \space \text{while} \space \space g(i, j) \ge \theta F=M∑N∑g(i,j)2 while g(i,j)≥θ
Thresholded pixel count
F = ∑ M ∑ N s ( g ( i , j ) , θ ) with s ( x , θ ) = { 0 , if x ≥ θ 1 , if x < θ F = \sum _M \sum _N s(g(i, j), \theta ) \space \space \space \space \text{with} \space \space s(x, \theta ) = \begin{cases} 0, & \text{ if } x \ge \theta \\ 1, & \text{ if } x < \theta \end{cases} F=M∑N∑s(g(i,j),θ) with s(x,θ)={0,1, if x≥θ if x<θ
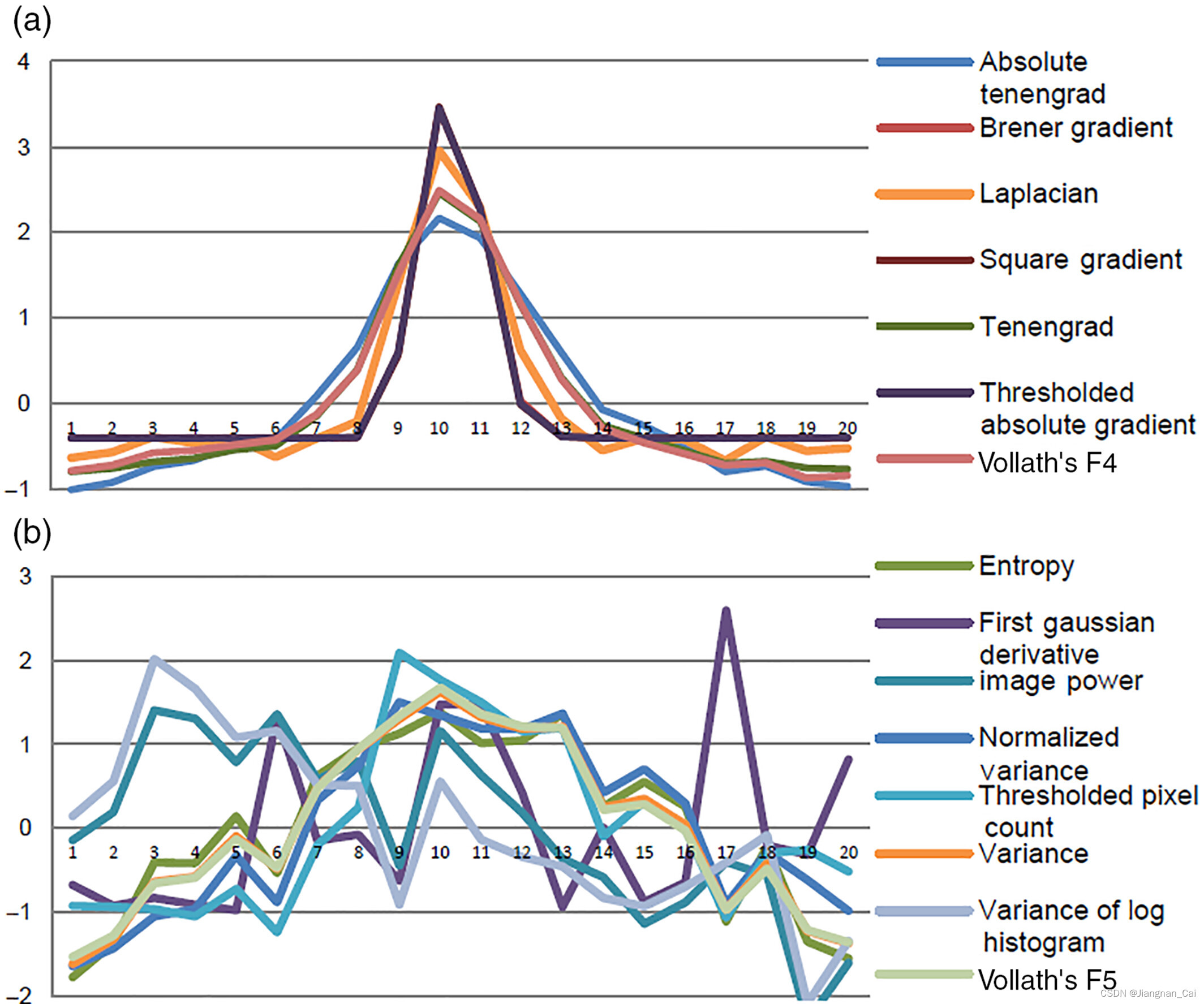
各种算法的对比
这个是基于他们的数据集得到的结果,可能在不同数据集,各个算法的表现不一样。看起来效果最好的是 absolute tenengrad 。
参考文献汇总
算法论文出处
- NRSS:一种针对图像模糊的无参质量评价指标
- SMD:光学显微镜自动聚焦算法研究
- SMD2:一种快速高灵敏度聚焦函数
- EAV:中巴地球资源一号卫星多光谱扫描图象质量评价
- PAV:图像清晰度评价方法研究
代码实现
- ENVIIDL 实现 PAV:利用ENVIIDL实现图像清晰度评价——点锐度算法
- C++ 实现 PAV:EVA改进(点锐度算法)图像清晰度评价方法C++实现
- Matlab实现:11种图像清晰度评价函数附MATLAB代码
- C++实现:无参考图像的清晰度评价方法及实现源码
其他
- SSIM 讲解:SSIM (Structure Similarity Index Measure) 结构衡量指标+代码
- 15种常见的清晰度评价指标:An algorithm selection methodology for automated focusing in optical microscopy