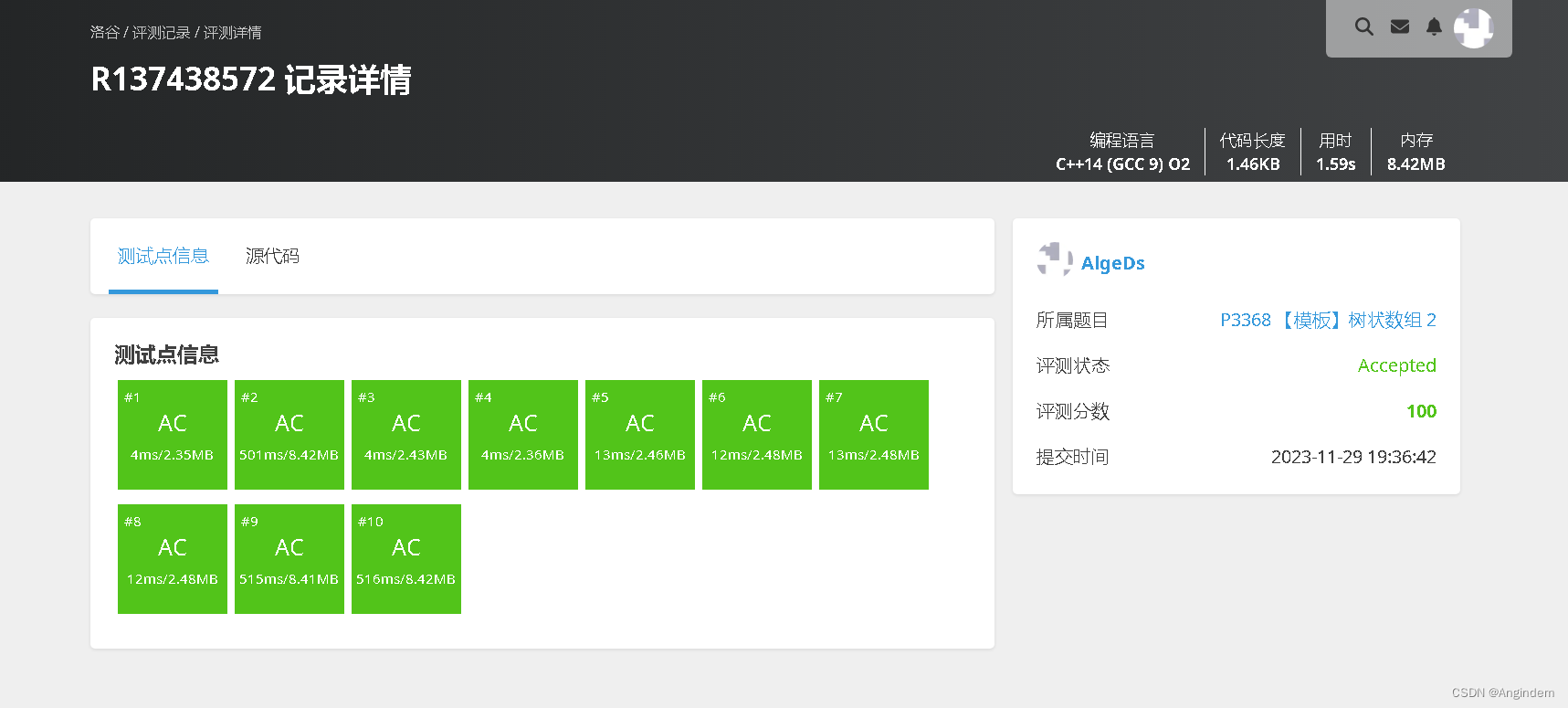
本题链接：【模板】树状数组 2 - 洛谷

题目：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

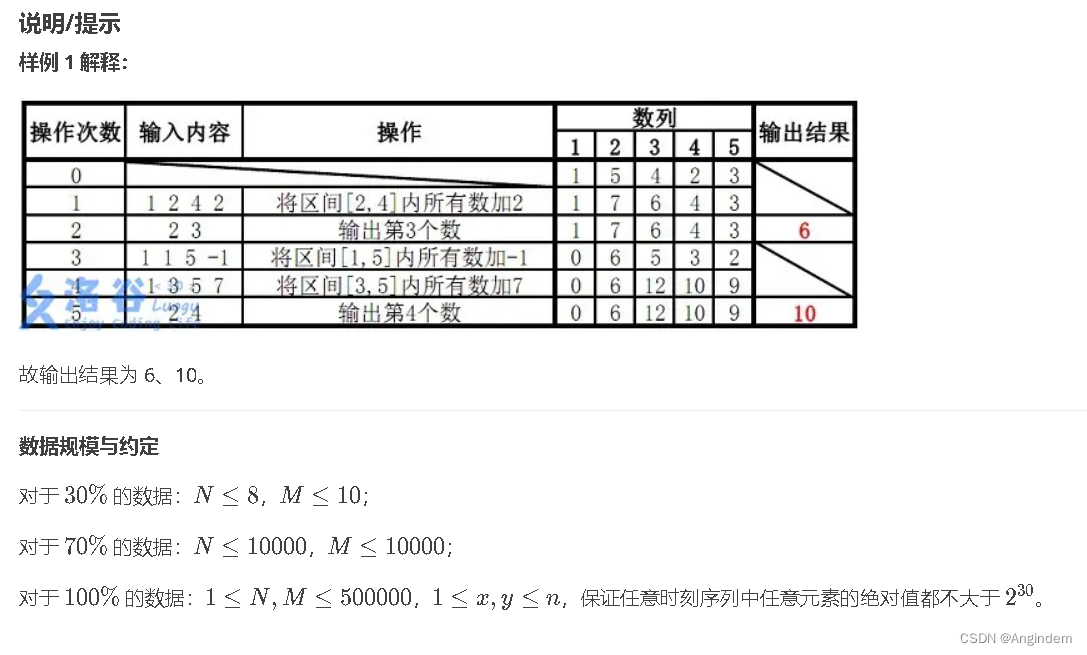
6
10

思路：

        根据题意，这里是需要区间添加值，单点查询值。如果区间添加值中暴力去一个个加值，肯定会TLE，所以我们这里运用到了模板树状数组的重要作用了。

        根据 差分 的性质，我们知道，区间加值，我们可以构造一个前缀和数组来表示当前原数组的元素值，对此，进行区间的修改，有效的避免O(n)的时间复杂度。

所以我们可以结合，树状数组的前缀和 + 差分 性质，达到区间修改，单点查询的效果。

下面给出操作函数：

// 单点添加元素
inline void Add_pos(int pos,int x)
{
	for(int i = pos;i <= n + 1;i+=lowbit(i)) arr[i] += x;
}

// 区间添加元素
inline void Add_section(int L,int R,int x)
{
	// 利用差分数组的原理，
	// 差分树状数组，
	// 达到区间修改值的效果
	Add_pos(L,x);
	Add_pos(R+1,-x);	
}

// 差分前缀和 单点查询
inline int Ask_pos(int pos)
{
	// 利用 差分 性质
	// 差分的前缀和，就是当前的元素值
	// 所以树状数组求前缀和，返回当前下标的元素值
	int ans = 0;
	for(int i = pos;i;i-=lowbit(i)) ans += arr[i];
	return ans;
}

代码详解如下：

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define lowbit(x) (x&(-x))
#define umap unordered_map
#define All(x) x.begin(),x.end()
//#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 7e7 + 10;

int n,m;
int arr[N];	// 构造 差分树状数组
int a[N];	// 记录原数组初始值

// 单点添加元素
inline void Add_pos(int pos,int x)
{
	for(int i = pos;i <= n + 1;i+=lowbit(i)) arr[i] += x;
}

// 区间添加元素
inline void Add_section(int L,int R,int x)
{
	// 利用差分数组的原理，
	// 差分树状数组，
	// 达到区间修改值的效果
	Add_pos(L,x);
	Add_pos(R+1,-x);	
}

// 差分前缀和 单点查询
inline int Ask_pos(int pos)
{
	// 利用 差分 性质
	// 差分的前缀和，就是当前的元素值
	// 所以树状数组求前缀和，返回当前下标的元素值
	int ans = 0;
	for(int i = pos;i;i-=lowbit(i)) ans += arr[i];
	return ans;
}

inline void solve()
{
	cin >> n >> m;
	for(int i = 1;i <= n;++i)
	{
		cin >> a[i];
		Add_pos(i,a[i] - a[i - 1]);	// 单点添加 初始值 的 差分元素
	}
	while(m--)
	{
		int op;
		cin >> op;
		if(op == 1)
		{
			int L,R,x;
			cin >> L >> R >> x;
			Add_section(L,R,x);	// 区间添加值	
		}else
		{
			int pos;
			cin >> pos;	// 差分前缀和单点查询
			cout << Ask_pos(pos) << endl;
		}
	}
}

signed main()
{
//	freopen("a.txt", "r", stdin);
//	IOS;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：