文章目录
- 前言
- 1. 希尔排序的思想
- 2. 希尔排序的一些小优化
前言
本章将详细介绍希尔排序的思想及实现,由于希尔排序是在插入排序的思想上进行升华,所以如果不知道插入排序或者不熟悉的可以先看看这篇文章:《简单排序》中的直接插入排序。
1. 希尔排序的思想
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成gap个组,所有距离为gap的数据分在同一组内,并对每一组内的记录进行排序。当gap组都排完以后,我们将gap缩小,重复上述分组和排序的工作。当gap = 1时(此时就是直接插入排序),所有记录在统一组内排好序。
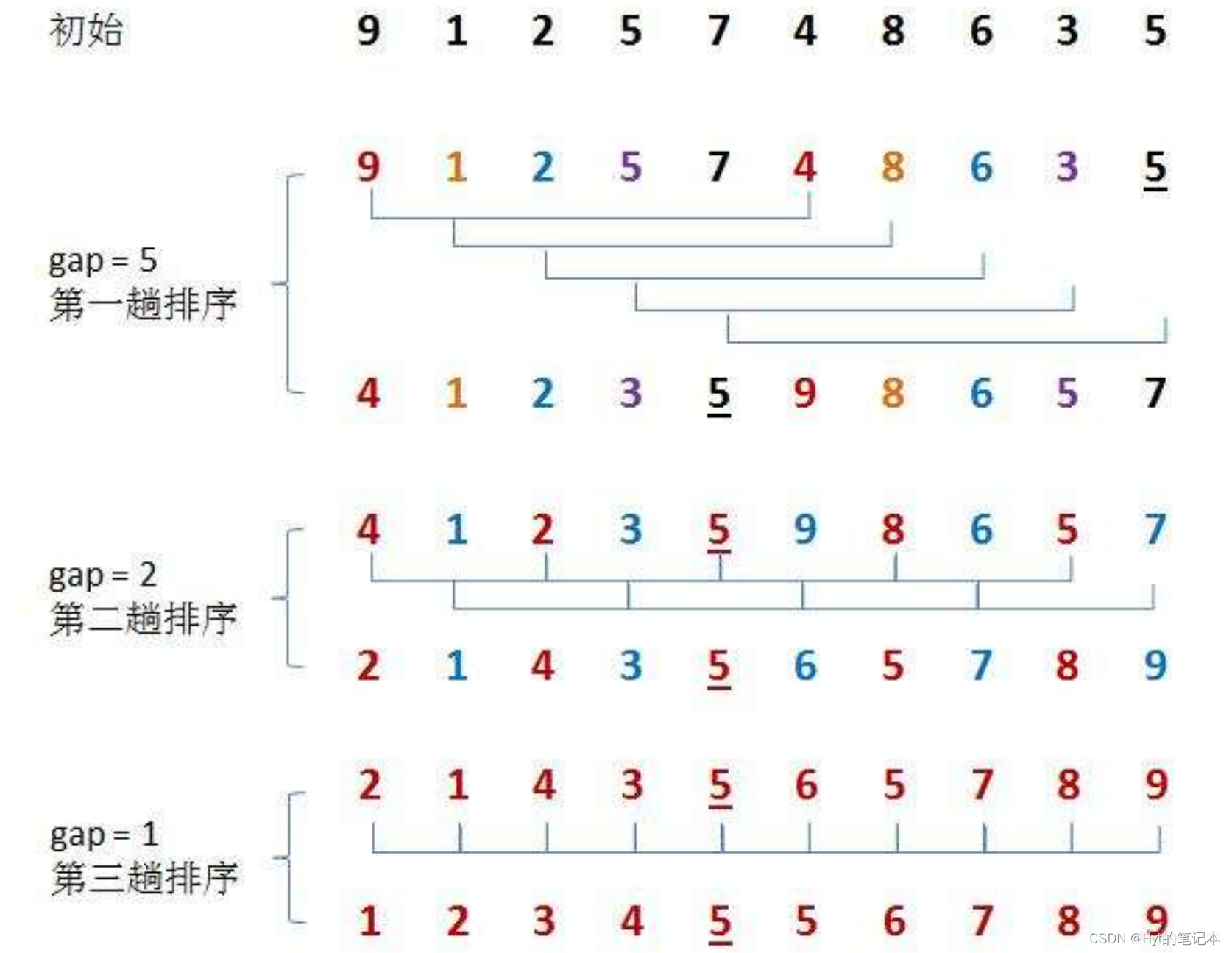
具体步骤如下图:
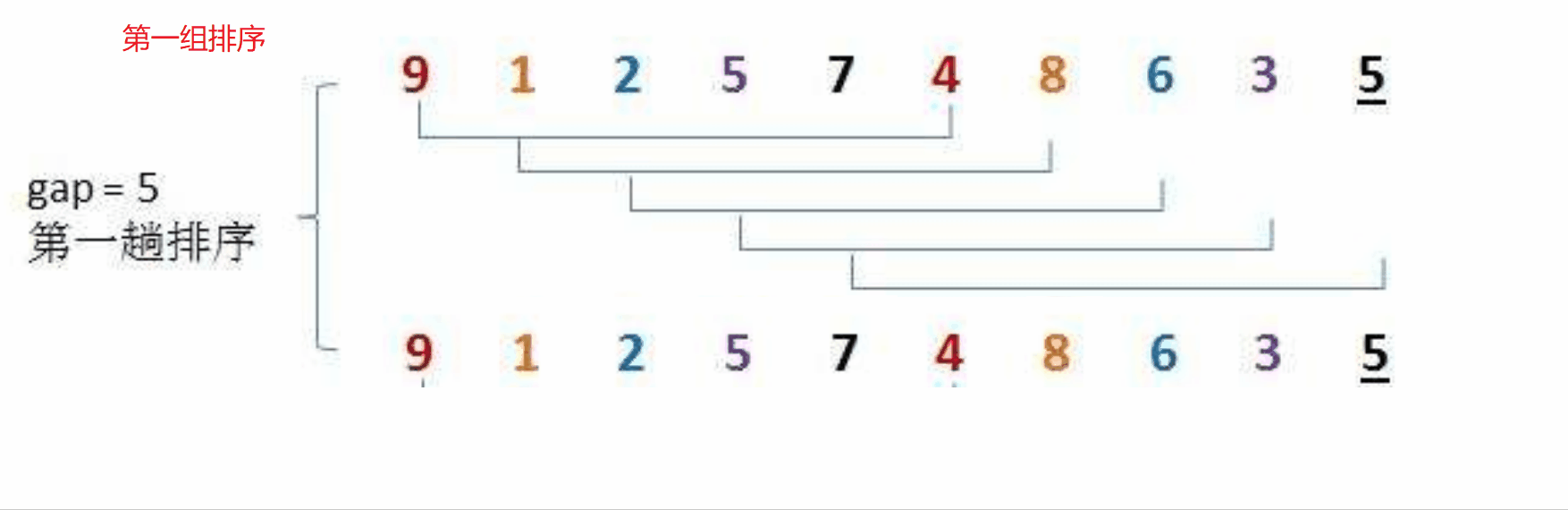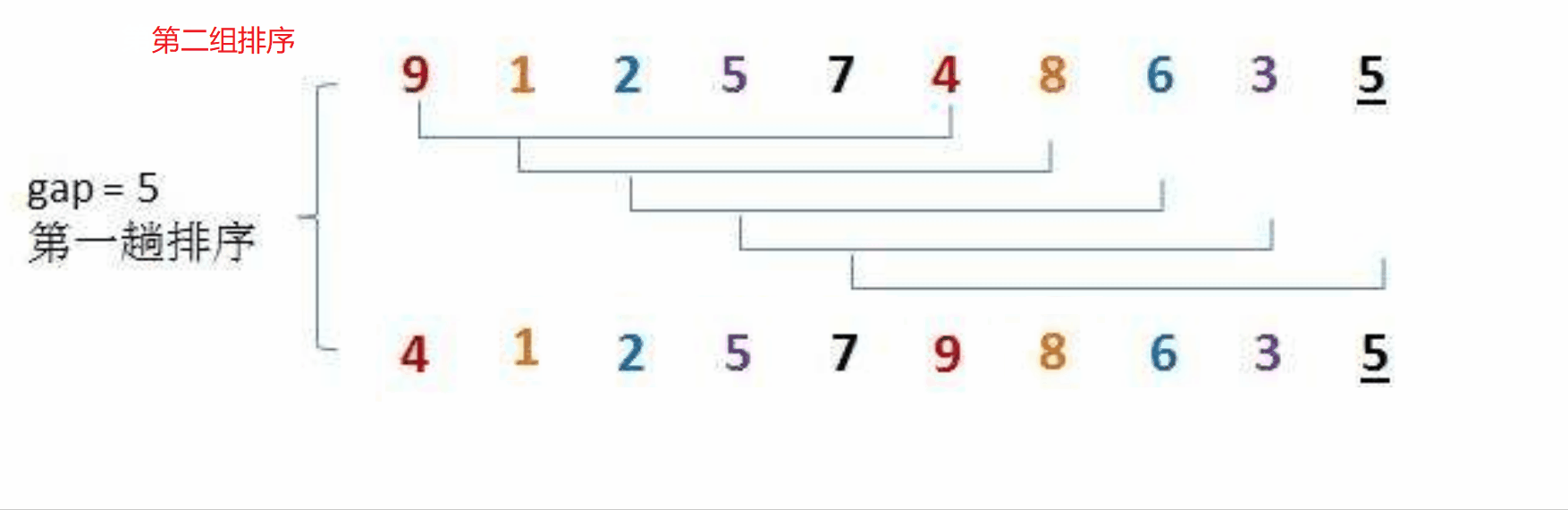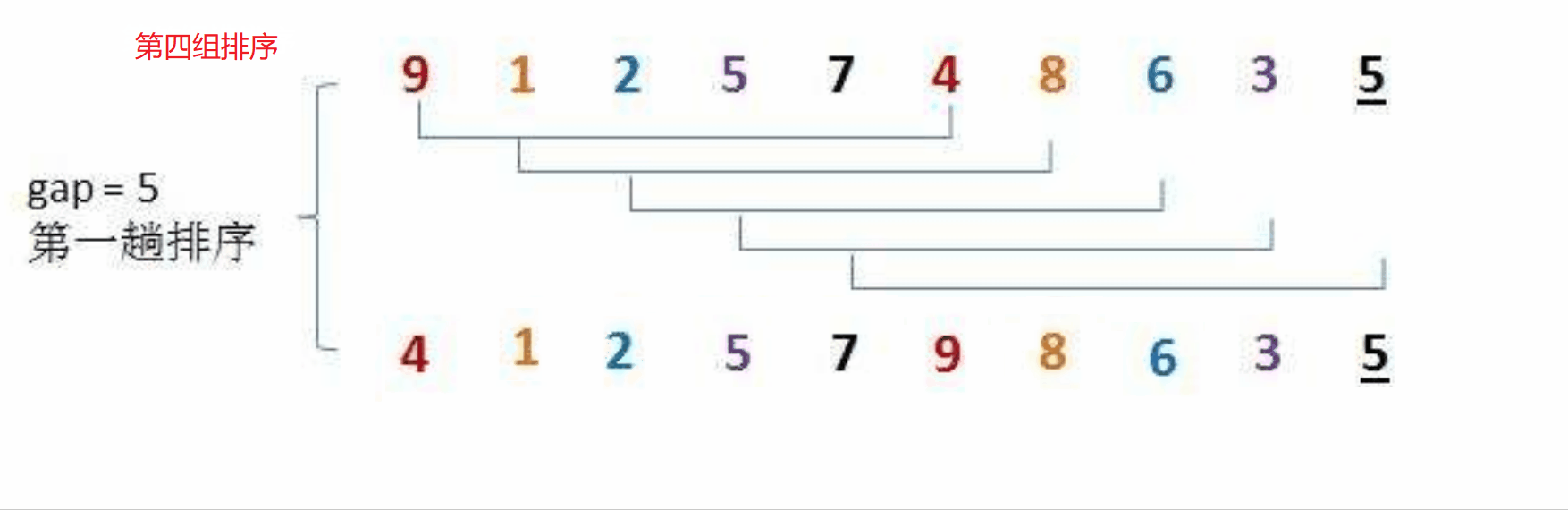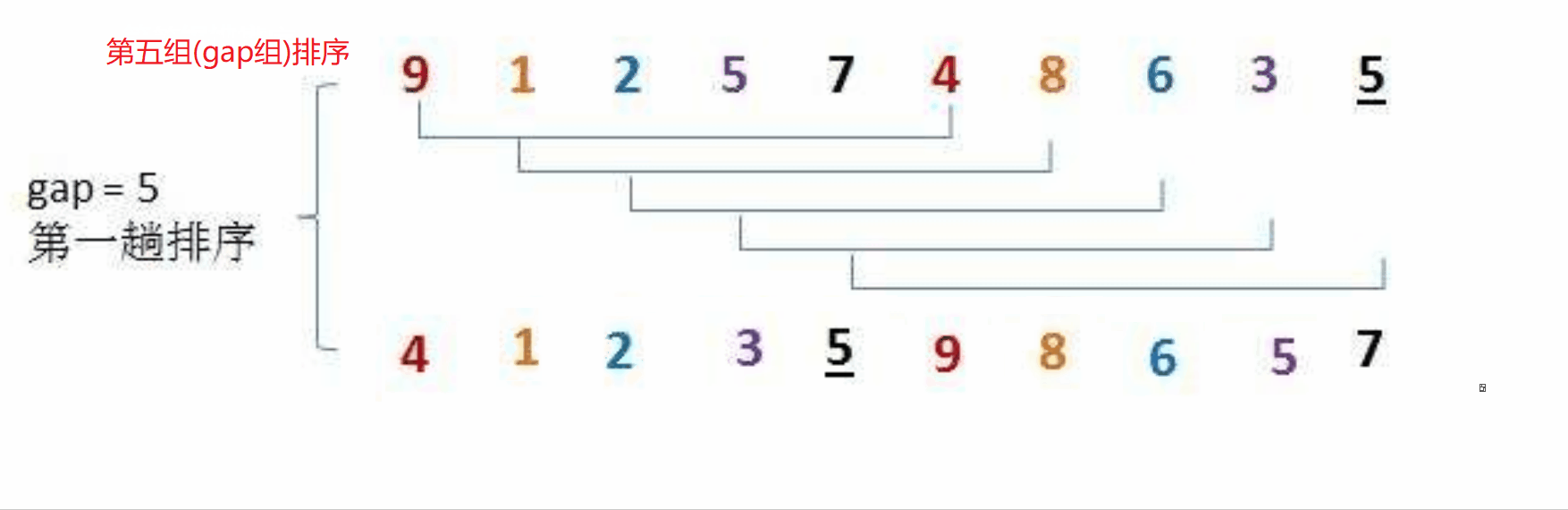
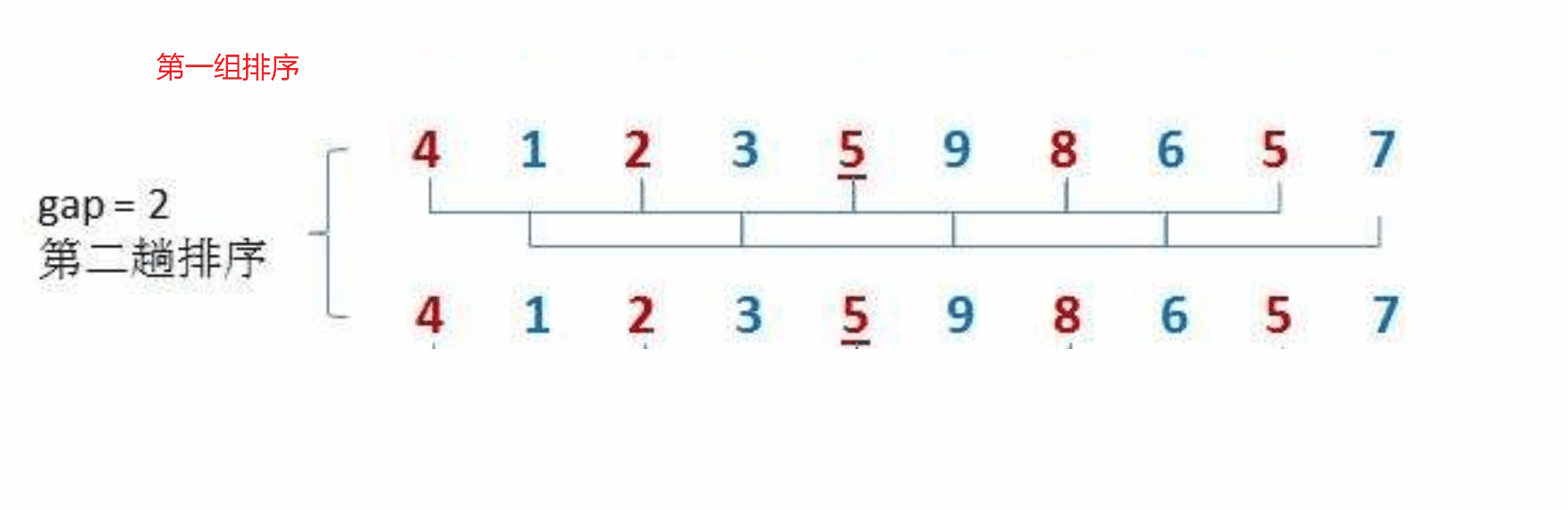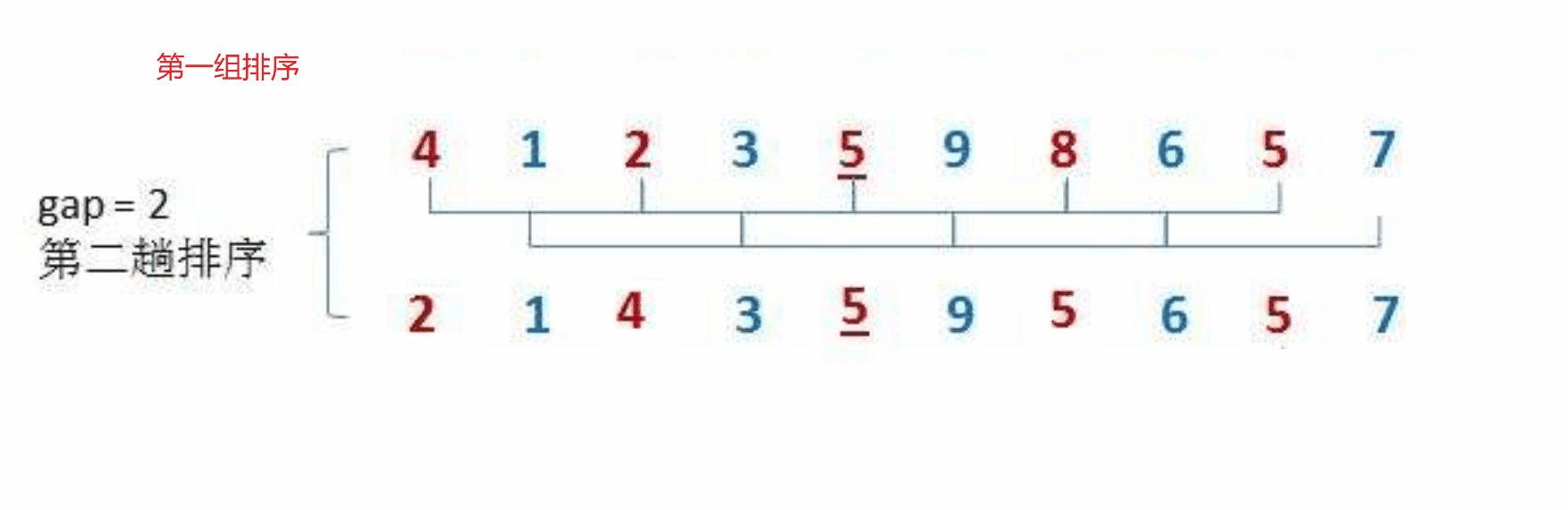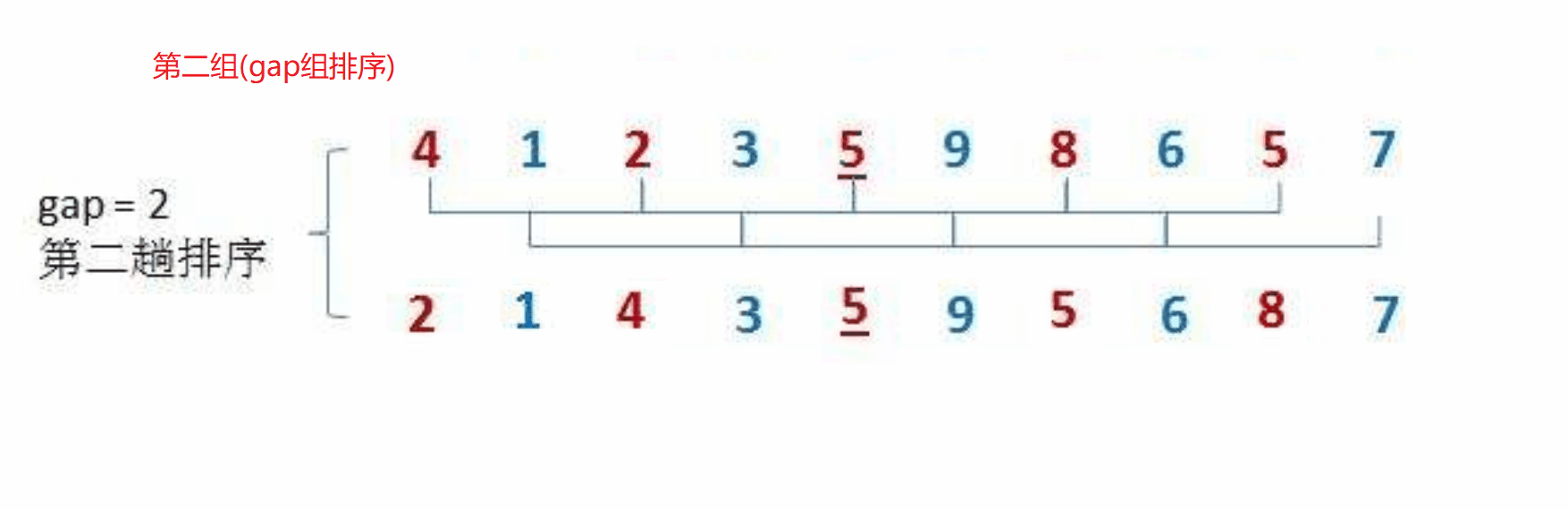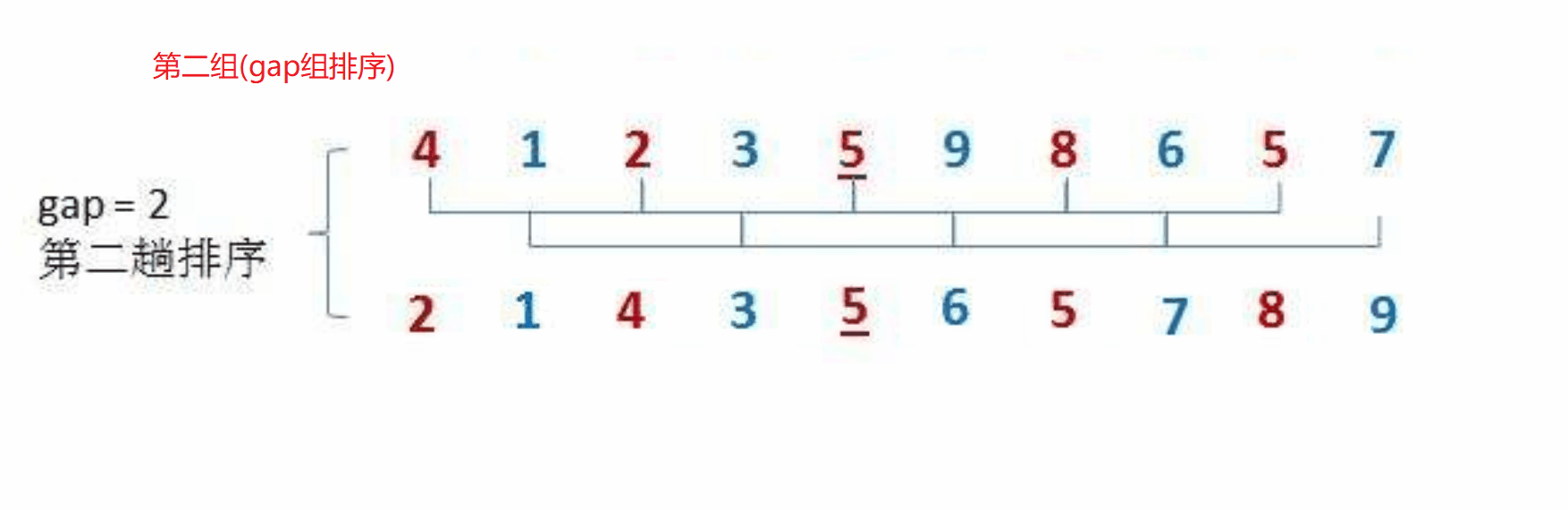
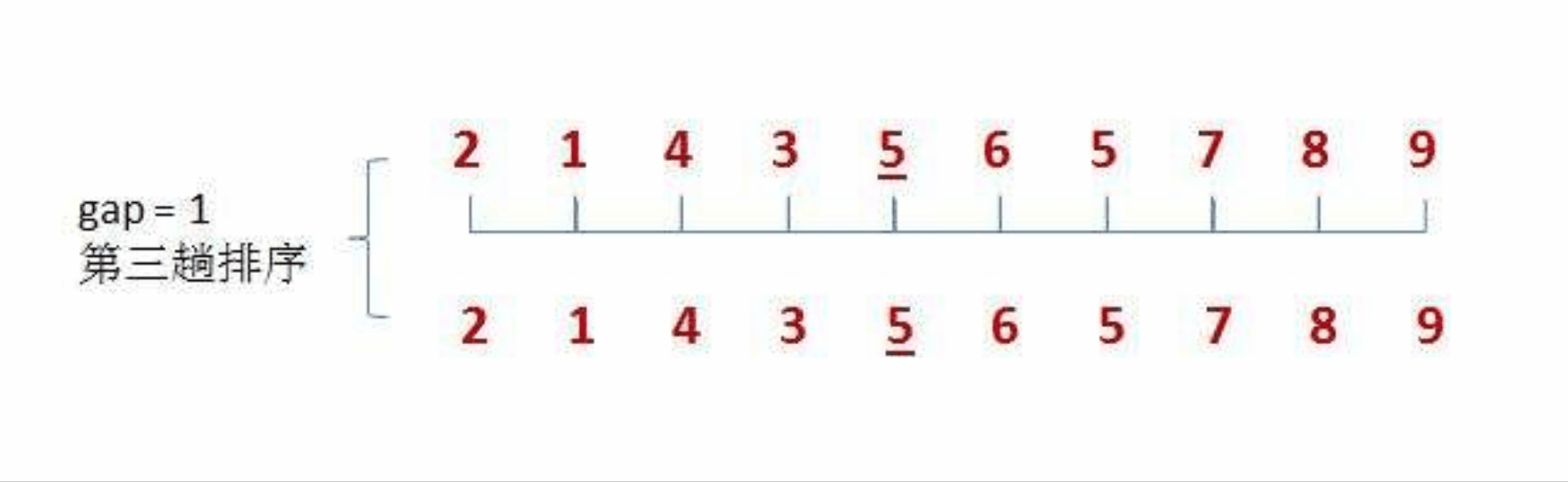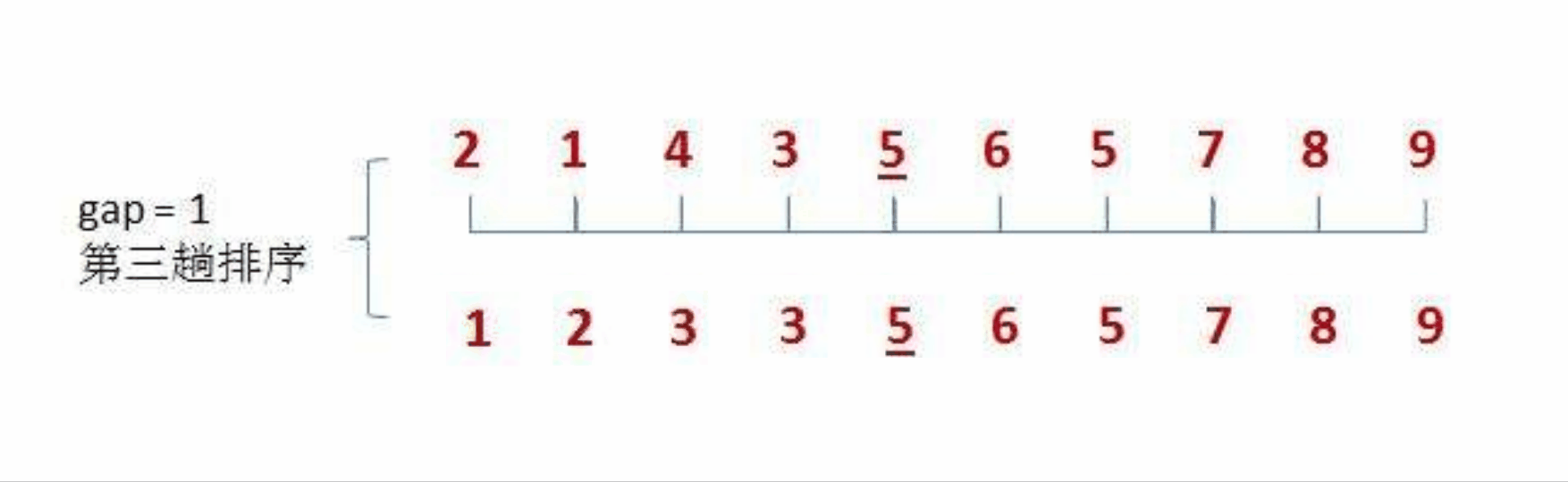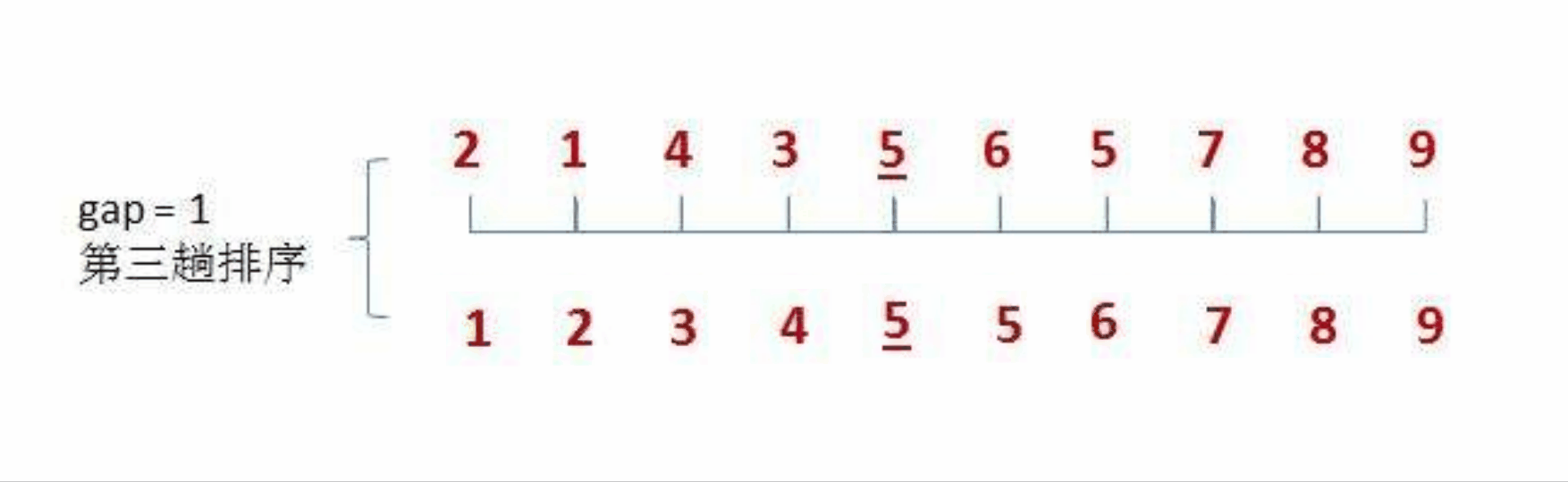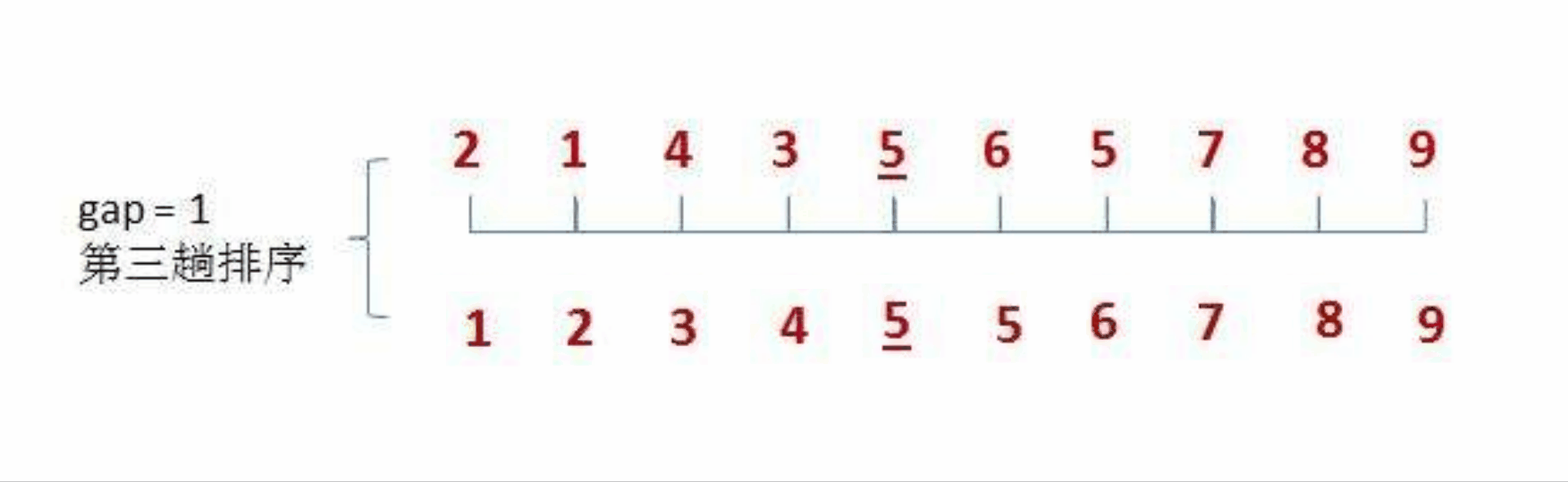
我们可以按照上面的思路,来用代码进行模拟实现:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 0)
{
// 每次gap/3 + 1,当gap为1时,就是选择排序
gap /= 2;
int count = 0;
// 调整几组取决于gap为多大
while (count < gap)
{
// 每组调整的步骤
for (int i = 0;i < n - gap;i += gap)
{
int tmp = a[i + gap]; // 定义一个临时值,用来保存每次要插入的数
int j = 0; //控制循环的变量
for (j = i;j >= 0;j -= gap)
{
// 从后面开始比,如果tmp比后面的数小,就将后面的数往后移gap
if (a[j] > tmp)
a[j + gap] = a[j];
else// 如果tmp比后面的数要大,就直接退出,因为我们是从第一个数开始这样操作的,前面能够保证是有序的
break;
}
a[j + gap] = tmp;
}
count++;
}
}
}
希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。
- 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的希尔排序的时间复杂度都不固定:
《数据结构(C语言版)》— 严蔚敏
《数据结构-用面相对象方法与C++描述》— 殷人昆

- 稳定性:不稳定
2. 希尔排序的一些小优化
我们上面那个实现的方式是取gap=[n / 2],gap=[gap / 2],直到gap=1,但我们看到 《数据结构-用面相对象方法与C++描述》— 殷人昆 中提到Hnuth取gap的方法,可以有一定程度上的提高我们的速度,具体是怎么提高的呢,因为这块涉及到很难的数学知识,目前还没人能够给出完整的数学分析,所以我们也不必去纠结,只要记住他们这些大佬经过多次实验提出的结论就可以了。
这里我打算进行两个优化:
- 就是gap的取值
- 我们上面每次排序是一组一组的排序,其实我们可以一次性全部排序完(这里效率上没有提升,只是代码量减少了)
具体代码如下:
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1) // gap最小等于1,所以这里的循环条件需要控制一下
{
// 每次gap/3 + 1,+1的目的是为了保证gap一定会等于1
gap = gap / 3 + 1;
// 我们将gap组一起调整
for (int i = 0;i < n - gap;++i)
{
int tmp = a[i + gap];// 定义一个临时值,用来保存每次要插入的数
int j = 0; // 控制循环的变量
for (j = i;j >= 0;j -= gap)
{
if (a[j] > tmp)
{
a[j + gap] = a[j];
}
else
break;
}
a[j + gap] = tmp;
}
}
}