系列文章目录
前言
在总结
2023华为软件精英挑战赛——全赛段思路分享与总结 - 知乎 (zhihu.com)时,发现自己还有很多技术细节没搞懂,这里看静态全局路径规划最常见的A*算法,这个博主讲得很好:
A-Star(A*)寻路算法原理与实现 - 知乎 (zhihu.com),demo码源,但是是C#,我有点不熟悉:
Demo/Assets/A-Star at master · luckyWjr/Demo (github.com)。还有几个可以看的资料:
A*寻路算法简洁源码及GIF原理演示(Lua)(C#) - 知乎 (zhihu.com)
Amit’s A* Pages (stanford.edu)。。。。
希望之后可以学一下D*和JPS:
最快速的寻路算法 Jump Point Search - 知乎 (zhihu.com)
一、A*算法是什么?
基于格子(Grid)
A*算法是一种基于格子(Grid)的寻路算法,也就是说会把我们的地图看作是由 w*h 个格子组成的,因此寻得的路径也就是由一连串相邻的格子所组成的路径。
优先搜索最有可能产生最佳路径的格子。A*正是这样的算法,因此可以避免掉很多歪路(不必要的计算),提高效率。
二、逻辑实现
估价函数
要对每个可能到达的格子进行估价,来判断应该先往哪个格子走,因此我们需要一个估价函数来计算。
对于任意一个格子n,其估价函数如下:
f(n) = g(n) + h(n)
其中 g(n) 指的是从起始格子到格子n的实际代价,而 h(n) 指的是从格子n到终点格子的估计代价。
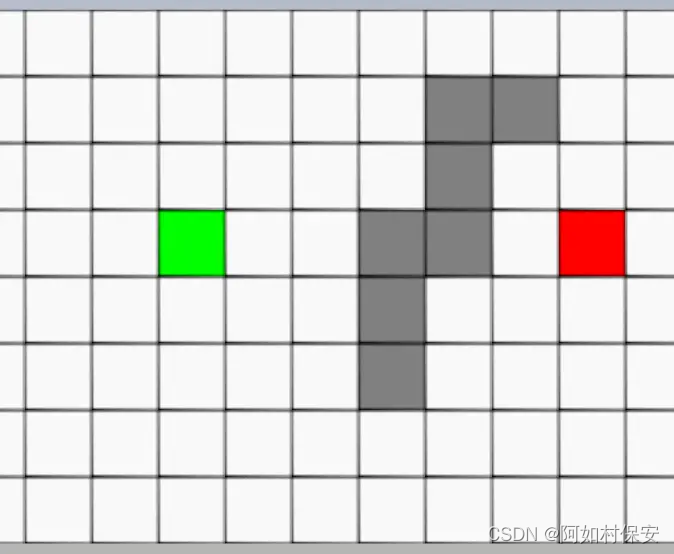
举个例子,我们来看看下面三个格子f(n)的值:
- 格子1:绿点到1要行动移动一格,因此 g(1)=1,格子1到红点的直线距离为6个格子,因此 h(1)=6,所以 f(1)=1+6=7 。
- 格子2:绿点到2要行动移动一格,因此 g(2)=1,格子2到红点的直线距离为4个格子,因此 h(2)=4,所以 f(2)=1+4=5 。
- 格子3:绿点到3要对角移动,因此 g(1)= 2 ,格子1到红点的直线距离为 17 (直角三角形斜边),因此h(3)= 17 ,所以 f(3)= 2+17 =5.54 。
可以看出,f(n) 的值基本代表着从起点格子到格子n再到终点这一段路径的长度。由于 f(2) < f(3) < f(1),因此我们优先应该考虑去往格子2的情况。
在上面,我们 h(n) 指的是格子与格子间的直线距离,也就是欧几里得距离,然而它有两个弊端:
- 计算过程中伴随着平方与开根号运算,并且需要使用浮点数,性能差。
- 实际过程中格子3并不能直接平滑的移动到红色格子,而需要水平+对角移动结合。即若没有障碍物,实际的 h(3) = 2 +3,而不是 17 。也就是说用欧几里得距离时, h(n) 的值永远小于或等于格子n到终点的最短实际距离。
因此针对上述这些问题,我们 h(n) 用的更多的是曼哈顿距离或者是对角线+直线的距离。
由于计算对角线同样需要开根号以及浮点数。为了加快计算,我们可以假设两个格子间的距离为10,然后直接认为对角线距离为14(不是根号200了),这样就可以避免浮点数和根号运算了。
总结来说:
- 如果 h(n) <= n到终点的实际距离,A*算法可以找到最短路径,但是搜索的点数多,搜索范围大,效率低。
- 如果 h(n) > n到终点的实际距离,搜索的点数少,搜索范围小,效率高,但是得到的路径并不一定是最短的。
- h(n) 越接近 n到终点的实际距离,那么A*算法越完美。(个人理解是如果用曼哈顿距离,那么只需要找到一条长度小于等于该距离的路径就算完成任务了。而使用对角线距离就要找到一条长度大于等于对角线距离且最短的路径才行。)
- 若 h(n)=0,即 f(n)=g(n),A*算法就变为了Dijkstra算法(Dijstra算法会毫无方向的向四周搜索)。
- 若 h(n) 远远大于 g(n) ,那么 f(n) 的值就主要取决于 h(n),A*算法就演变成了BFS算法。
因此在启发式搜索中,估价函数是十分重要的,采用了不同的估价可以有不同的效果。
具体寻路过程
一些基本的概念介绍完后,我们来看看怎么A*算法的具体寻路是怎么样的,基本上就是说,哪些格子我们要去估价,然后这些格子按什么顺序去估价。
我们从最简单的场景入手来理解,如下图:

第一步:因为我们的绿点可以往周边8个格子移动,那么我们就要用估价函数计算它周边格子的值,来看看往哪走比较好,得到结果如下(使用对角线距离估价):

因为我们是通过绿色格子计算得到这8个格子的,因此它们都指向绿色格子(格子中的箭头),或者称绿色格子是它们的parent。
第二步:我们找到第一步8个格子中f(n)值最小的格子(格子0),然后再计算它周边格子的f(n),如下图:

此时格子0周边格子的g(n)应该是g(0)的值加上自己到格子0的距离。例如格子1此时的g(1)应该为g(0)+14=24,即2-0-1的顺序。但是由于格子1在第一步已经算过了,当时g(1)=10,2-1的顺序。这里我们要用较小的那个值,因为g值小,说明路径短。格子3,4,5同理。而格子6之前没有计算过,因此f(6)=g(6)+h(6)=(g(0)+14)+h(h),顺序2-0-6。
格子7,8由于是障碍物,直接不管就行。格子2由于之前已经计算过它周边了,没有再计算它的意义了,也不用管。
第三步:我们从剩下的8个深蓝色的格子中再找出f(n)最小的格子,由于有3个等于58的格子,我们随便取一个计算它周边的格子,如下图:

这里可以发现,格子1的g值并不是最小的,但是不要紧,当我们后面计算到格子2时,会更新格子1的g值(前面说了会用较小的g值),并且箭头指向格子2。
第四步...第n步:一直找出深蓝色格子中的f(n)最小的格子,然后计算周边格子的估价值。
最后一步:当我们发现某个格子(格子1)周边有个格子是终点格子时,就说明我们找到了到终点的最短路径。

我们只需要根据格子1的箭头指向一直往前就可以得到完整的路径:

三、代码实现
首先由于我们要记录格子的估价值,以及它的parent,因此需要一个类来存储这些值:
public class Node
{
Int2 m_position;//下标
public Int2 position => m_position;
public Node parent;//上一个node
//角色到该节点的实际距离
int m_g;
public int g {
get => m_g;
set {
m_g = value;
m_f = m_g + m_h;
}
}
//该节点到目的地的估价距离
int m_h;
public int h {
get => m_h;
set {
m_h = value;
m_f = m_g + m_h;
}
}
int m_f;
public int f => m_f;
public Node(Int2 pos, Node parent, int g, int h) {
m_position = pos;
this.parent = parent;
m_g = g;
m_h = h;
m_f = m_g + m_h;
}
}
然后我们需要两个数据结构open和close来存储格子,在之前的过程中,将要被计算周边格子的格子都存储在open当中,当周边格子计算完后,就可以把这个格子存储到close中,然后把它周边的格子再放入到open中。
例如一开始我们把起始格子放入open中,然后从open中取出f(n)值最小的一个格子(这里使用C#的Linq排序)去计算它周边的格子。因为此时open中只有一个元素,因此就是计算起始格子周边的格子。接着把起始格子周边8个格子加入到open中,把起始格子从open中删除加入到close中。
然后再从open中找出f(n)最小的格子,将它周边的格子加入到open中,并将自己从open中删除加入到close中,如此循环。
再每次计算周边格子的时候,需要判断这些格子是否超出边界,是否是障碍物,是否在close中,这三种情况不需要再处理该格子了。如果格子已经在open中,就要像之前所说的,若新的g值小于老的g值,就要更新g、f 以及parent的值。
最后如果周边某个格子是终点(代表寻路完成)或者open列表为空(代表可用格子全部计算完,但却没找到终点,死路一条!),则结束寻路过程。
可以发现整个过程都要频繁的用到了增删以及查询,因此open和close使用了Dictionary。
代码如下:
public class AStar {
static int FACTOR = 10;//水平竖直相邻格子的距离
static int FACTOR_DIAGONAL = 14;//对角线相邻格子的距离
bool m_isInit = false;
public bool isInit => m_isInit;
UIGridController[,] m_map;//地图数据
Int2 m_mapSize;
Int2 m_player, m_destination;//起始点和结束点坐标
EvaluationFunctionType m_evaluationFunctionType;//估价方式
Dictionary<Int2, Node> m_openDic = new Dictionary<Int2, Node>();//准备处理的网格
Dictionary<Int2, Node> m_closeDic = new Dictionary<Int2, Node>();//完成处理的网格
Node m_destinationNode;
public void Init(UIGridController[,] map, Int2 mapSize, Int2 player, Int2 destination, EvaluationFunctionType type = EvaluationFunctionType.Diagonal) {
m_map = map;
m_mapSize = mapSize;
m_player = player;
m_destination = destination;
m_evaluationFunctionType = type;
m_openDic.Clear();
m_closeDic.Clear();
m_destinationNode = null;
//将起始点加入open中
AddNodeInOpenQueue(new Node(m_player, null, 0, 0));
m_isInit = true;
}
//计算寻路
public IEnumerator Start() {
while(m_openDic.Count > 0 && m_destinationNode == null) {
//按照f的值升序排列
m_openDic = m_openDic.OrderBy(kv => kv.Value.f).ToDictionary(p => p.Key, o => o.Value);
//提取排序后的第一个节点
Node node = m_openDic.First().Value;
//因为使用的不是Queue,因此要从open中手动删除该节点
m_openDic.Remove(node.position);
//处理该节点相邻的节点
OperateNeighborNode(node);
//处理完后将该节点加入close中
AddNodeInCloseDic(node);
yield return null;
}
if(m_destinationNode == null)
Debug.LogError("找不到可用路径");
else
ShowPath(m_destinationNode);
}
//处理相邻的节点
void OperateNeighborNode(Node node) {
for(int i = -1; i < 2; i++) {
for(int j = -1; j < 2; j++) {
if(i == 0 && j == 0)
continue;
Int2 pos = new Int2(node.position.x + i, node.position.y + j);
//超出地图范围
if(pos.x < 0 || pos.x >= m_mapSize.x || pos.y < 0 || pos.y >= m_mapSize.y)
continue;
//已经处理过的节点
if(m_closeDic.ContainsKey(pos))
continue;
//障碍物节点
if(m_map[pos.x, pos.y].state == GridState.Obstacle)
continue;
//将相邻节点加入open中
if(i == 0 || j == 0)
AddNeighborNodeInQueue(node, pos, FACTOR);
else
AddNeighborNodeInQueue(node, pos, FACTOR_DIAGONAL);
}
}
}
//将节点加入到open中
void AddNeighborNodeInQueue(Node parentNode, Int2 position, int g) {
//当前节点的实际距离g等于上个节点的实际距离加上自己到上个节点的实际距离
int nodeG = parentNode.g + g;
//如果该位置的节点已经在open中
if(m_openDic.ContainsKey(position)) {
//比较实际距离g的值,用更小的值替换
if(nodeG < m_openDic[position].g) {
m_openDic[position].g = nodeG;
m_openDic[position].parent = parentNode;
ShowOrUpdateAStarHint(m_openDic[position]);
}
}
else {
//生成新的节点并加入到open中
Node node = new Node(position, parentNode, nodeG, GetH(position));
//如果周边有一个是终点,那么说明已经找到了。
if(position == m_destination)
m_destinationNode = node;
else
AddNodeInOpenQueue(node);
}
}
//加入open中,并更新网格状态
void AddNodeInOpenQueue(Node node) {
m_openDic[node.position] = node;
ShowOrUpdateAStarHint(node);
}
void ShowOrUpdateAStarHint(Node node) {
m_map[node.position.x, node.position.y].ShowOrUpdateAStarHint(node.g, node.h, node.f,
node.parent == null ? Vector2.zero : new Vector2(node.parent.position.x - node.position.x, node.parent.position.y - node.position.y));
}
//加入close中,并更新网格状态
void AddNodeInCloseDic(Node node) {
m_closeDic.Add(node.position, node);
m_map[node.position.x, node.position.y].ChangeInOpenStateToInClose();
}
//寻路完成,显示路径
void ShowPath(Node node) {
while(node != null) {
m_map[node.position.x, node.position.y].ChangeToPathState();
node = node.parent;
}
}
//获取估价距离
int GetH(Int2 position) {
if(m_evaluationFunctionType == EvaluationFunctionType.Manhattan)
return GetManhattanDistance(position);
else if(m_evaluationFunctionType == EvaluationFunctionType.Diagonal)
return GetDiagonalDistance(position);
else
return Mathf.CeilToInt(GetEuclideanDistance(position));
}
//获取曼哈顿距离
int GetDiagonalDistance(Int2 position) {
int x = Mathf.Abs(m_destination.x - position.x);
int y = Mathf.Abs(m_destination.y - position.y);
int min = Mathf.Min(x, y);
return min * FACTOR_DIAGONAL + Mathf.Abs(x - y) * FACTOR;
}
//获取对角线距离
int GetManhattanDistance(Int2 position) {
return Mathf.Abs(m_destination.x - position.x) * FACTOR + Mathf.Abs(m_destination.y - position.y) * FACTOR;
}
//获取欧几里得距离,测试下来并不合适
float GetEuclideanDistance(Int2 position) {
return Mathf.Sqrt(Mathf.Pow((m_destination.x - position.x) * FACTOR, 2) + Mathf.Pow((m_destination.y - position.y) * FACTOR, 2));
}
public void Clear() {
foreach(var pos in m_openDic.Keys) {
m_map[pos.x, pos.y].ClearAStarHint();
}
m_openDic.Clear();
foreach(var pos in m_closeDic.Keys) {
m_map[pos.x, pos.y].ClearAStarHint();
}
m_closeDic.Clear();
m_destinationNode = null;
m_isInit = false;
}
}同时这里,如果f相同,就取H小的,这样会更优
修改代码如下:
//先按照f的值升序排列,当f值相等时再按照h的值升序排列
m_openDic = m_openDic.OrderBy(kv => kv.Value.f).ThenBy(kv => kv.Value.h).ToDictionary(p => p.Key, o => o.Value);总结
多研究下路径规划算法,同时要落实细节,今天这个代码就看得很舒服。