长度最小的数组

长度最小的数组

题目描述

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

解法

暴力解法

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result = Integer.MAX_VALUE;
        for(int i = 0; i < nums.length; i++){
            int sum = 0;
            for(int j = i; j < nums.length; j++){
                sum += nums[j];
                if(sum >= target){
                    result = Math.min(result,j - i + 1);
                    break;
                }
            }
        }
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

这种做法可以很容易想到，可是谁想到它…

超时了哈哈😓😓😓😓😓😓😓😓

---

那么下面我们看看另外一种思路。

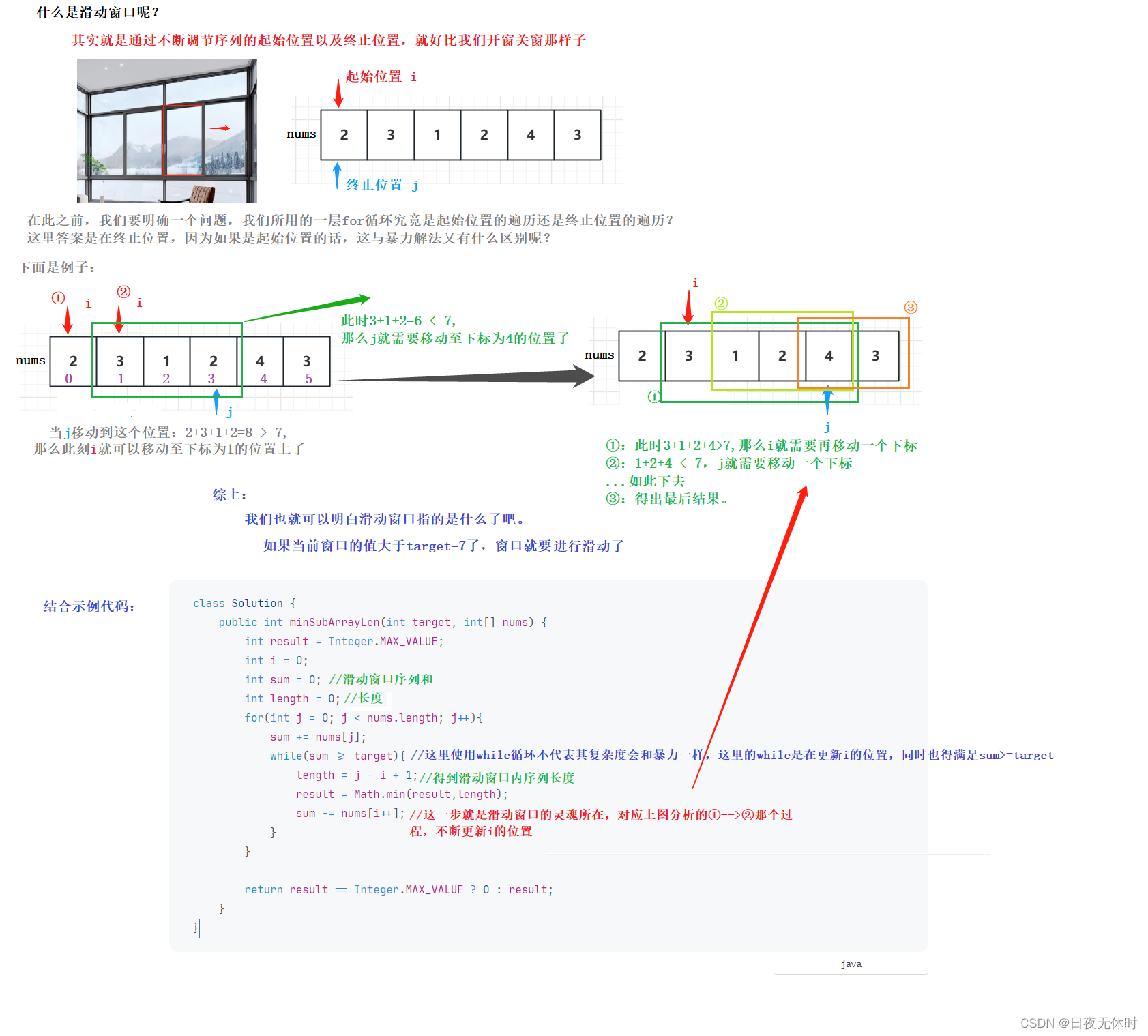
滑动窗口

先看示例代码：

Java示例代码

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result = Integer.MAX_VALUE;
        int i = 0;
        int sum = 0;
        int length = 0;
        for(int j = 0; j < nums.length; j++){
            sum += nums[j];
            while(sum >= target){
                length = j - i + 1;
                result = Math.min(result,length);
                sum -= nums[i++];
            }
        }
 
        return result == Integer.MAX_VALUE ? 0 : result;
    }
}

下面见分析：

c++示例代码

class Solution
{
public:
	int minSubArrayLen(int target, vector<int>& nums)
	{
		int n = nums.size(), sum = 0, len = INT_MAX;
		for (int left = 0, right = 0; right < n; right++)
		{
			sum += nums[right]; // 进窗⼝
			while (sum >= target) // 判断
			{
				len = min(len, right - left + 1); // 更新结果
				sum -= nums[left++]; // 出窗⼝
			}
		}
		return len == INT_MAX ? 0 : len;
	}
};