自己动手写 chatgpt: Attention 机制的原理与实现

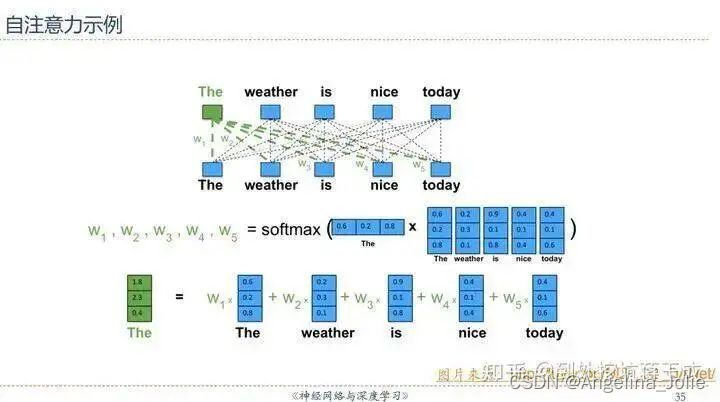
chatgpt等大模型之所以成功都有赖于一种算法突破，那就是 attention 机制。这种机制能让神经网络更有效的从语言中抽取识别其内含的规律，同时它支持多路并行运算，因此相比于原来的自然语言处理算法，它能够通过并发的方式将训练的速度提升几百倍，于是海量的训练数据，加上超大规模的算力，并利用超大规模的并行计算来推进网络的训练成为可能，这个机制没有发明之前，原有算法根本无法实现并行运算，因此网络的训练效率极低，这也是为何使用了 attention 机制的网络其能力要远远超于原有模型的原因。

那么什么叫 attention 机制呢，如果你在网上搜索会发现相关内容汗牛充栋，但我觉得能够将其说清楚的很少，你要想了解它的原理，你需要有很好的数学基础，我在这里尝试利用更加通俗的语言来说明它，在没有严谨数学逻辑推导的情况下，普通语言的逻辑描述必然会挂一漏万，但主要目的是能给大家一个基本的感性认识，后面我们会利用代码实践的方式增强我们在理性上对该算法的理解。

所谓 attention 机制，本质上是一种“和稀泥”。由于计算机基于 0,1 二进制，因此结果不是 0 就是 1，其中没有灰色地带，但这种”一言九鼎“的结论不能适用于深度学习，有过深度学习经验的同学可以看到，网络给出的答案往往都基于概率，在应用上我们选取其概率最大的结论最为最终结果。attention 机制本质在于给多个可能的答案分配一个比率，然后这些比率与对应答案相乘，最后加总起来成为最终答案。

举个具体例子。假设我们要预测一对夫妇他们孩子在 10 岁时的生长状况。首先我们要用一种数学方式来描述所谓的”生长状况“，在深度学习中我们经常使用向量来表示需要描述的对象。因此我们用一个向量来描述孩子的“生长状况”,例如 V(孩子)={身高，体重，脸型，心率，心理状态，健康状态…}，也就是说我们使用一系列指标组合成的向量来描述孩子的情况。现在问题在于我们如何得出 V(10 岁的孩子）这个向量里面的各个分量数值呢。一个直白的方法是，我们取出孩子爸爸，妈妈，爷爷，奶奶，外公，外婆，叔叔，姑姑，舅舅，大姨，小姨等人在 10 岁时的对应向量，把这些向量按照”一定比例“进行加总，所得的结果向量就可以作为孩子 10 岁时的”生长状况“向量。

现在有过问题就是如何确定”一定比例“，爸爸对应的向量占比多少，妈妈对应向量占比多少，爷爷奶奶和其他亲戚的向量占比多少呢？显然爸爸妈妈作为直接双亲，所占比率一定会大一些，亲缘关系越远，所占比率自然就要相应的降低。这里还有一个问题就是，我们要推测的孩子是男孩还是女孩，孩子性别不同，各个亲人对应的向量比率就得发生相应的变化。我们使用变量 query 来表示要推测的孩子信息，例如 query(男孩)表示要推测男孩子 10 岁时生长情况，query(女孩)表示推测女孩 10 岁时的生长状况。

假设我们现在有一个函数f能计算出对应亲戚向量的比率，例如 f(query(男孩), V(爸爸)) = a1，表示我们要推测男孩十岁时生长情况时，爸爸10 岁时“生长情况”向量的占比是 a1,于是我们分别计算 f(query(男孩),v(妈妈))=a2,…f(query(男孩),v(小姨))=a11, 其中 a1 + a2 +… + a11 = 1，于是我们就可以推算男孩 10 岁时”生长情况“向量为 a1V(爸爸)+a2V(妈妈)+…+a11*V(小姨)。

上面算法中,用于在 f 中计算占比值的 v(爸爸),v(妈妈）等向量我们统一用 key 来表示，在最后加总”和稀泥“中所使用的 v(爸爸),v(妈妈)等向量，我们用 value 来表示，很显然这里 key 对应的集合对象和 value 对应的集合对象是同一种，这种情况就叫做 self-attention，很多应用场景下,key 和 value 对应的对象很可能不同，对于自然语言处理，例如 chatgpt，它使用的就是 self-attention 机制，也就是 key 和 value 是同一个集合。

在上面的算法中其实还存在很大问题，那就是有很多影响因素没有考虑到。例如男孩所在的国家，民族，时代，社会经济发展，所属民族文化，父母亲戚的国籍，家庭财务状况，家人受教育状况等一系列因素，我们预测一个长在瑞士的孩子，和一个长在阿富汗的孩子，其结果肯定有很大差异，这些差异就是由各种外在影响因素造成，问题在于如何计算这些差异的影响呢？首先一个难题在于我们如何知道到底有哪些外在因素会对孩子的成长造成影响，由于我们无法仔细的穷尽所有外在影响因素，因此在深度学习算法上，通常采用一个矩阵来表示，矩阵的规模越大，它就越能囊括可能的影响，从而预测的结果就越准确。我们使用 Wq 来表示未知因素对孩子的影响，这些因素肯定也会影响到对应亲人的影响比率，所以我们使用 Wk 表示在计算比率时相应亲人所收到的影响，于是上面 f(query(男孩),v(爸爸))就变成 f(Wqquery(男孩),Wkv(爸爸))，其他亲戚的比率运算也要同样乘以对应矩阵。最后这些因素也会影响到”和稀泥“的过程，我们用 Wv 来表示相关因素对和稀泥的影响，于是 a1*(WvV(爸爸))+a2(WvV(妈妈))+…+a11(Wv*V(小姨))

以上所描述的流程就是 attention 机制的”说人话“描述。算法的任务就是通过大量的数据推算出 Wq, Wk, Wv，确定了这些变量后，我们就能通过运算来得出相应结果。在自然语言处理中，句子中词语的理解其实要根据同一句子中其他词语来理解，例如 apple 这个单词，你觉得它应该对应水果的苹果，还是对应科技巨头苹果？显然我们需要通过句子的上下文来判断，对应句子，please buy a bag of apple and orange，这里面的 apple 就是水果，为何我们能如此确定呢，因为 bag 和 orange 的存在确定了它的含义，这里 apple对应的就是 query，其他所有单词都对应 key和 value，其中 apple 和 bug, orange 的关系最大，其他单词与它的联系就很小，于是我们想要让计算机理解这里的 apple，那就是让计算机计算 a1v(please) + a2v(buy)+…a4v(bag)+…a6V(apple)+…+a8*(orange)，由于 please,buy 等词对 apple 含义的影响很低，因此他们对应影响系数的值需要很小，但是单词 bag，orange 影响很大，因此对应系数就会比较大，apple 这个词本身对计算机理解它帮助也不大，因此对应系数也会很小。同理对于句子 apple released new phone，其中单词 phone 对 apple 的理解影响很大，通过这个词我们能确定这里的 apple 对应的是科技公司而不是水果，因此”和稀泥“的时候,phone 对应的系数就会很大。

基于以上论述，我们通过代码来模拟一下整个 self-attention 算法流程。首先我们用向量来表示句子中的单词，前面章节我们看到单词对应向量的长度可能很大，这里我们我们只需要了解原理，因此使用长度为 4 的向量来表示单词：

import numpy as np
print("步骤 1，随机生成 3 个长度为 4 的向量来表示含有三个单词的句子")
#向量的数值不重要
x = np.array(
    [
        [1.0, 0.0, 1.0, 0.0],
        [0.0, 2.0, 0.0, 2.0],
        [1.0, 1.0, 1.0, 1.0]
    ]
)
print(x)

上面代码运行后结果为：

步骤 1，随机生成 3 个长度为 4 的向量来表示含有三个单词的句子
[[1. 0. 1. 0.]
 [0. 2. 0. 2.]
 [1. 1. 1. 1.]]

我们用图形来表达相关流程，通过图形的变化我们能更容易掌握算法流程，首先是初始化三个单词向量：
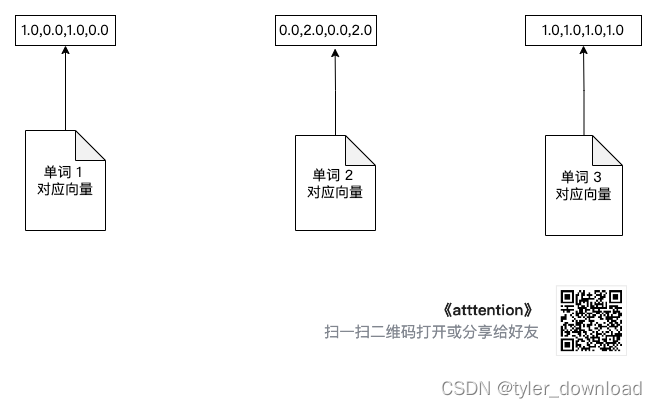
请添加图片描述

第二部初始化前面描述过的 Wq, Wv, Wk，同理他们内部分量的值一点也不重要，神经网络会通过训练来确认他们的具体值:

print("步骤 2，确认 Wq, Wv, Wk，由于要跟上面向量做乘法，因此他们的行数是 4，列数可以任意取值，注意 w_query 和 w_key 列数取值要相同")
w_query = np.array([
    [1, 0, 1],
    [1, 0, 0],
    [0, 0, 1],
    [0, 1, 1]
])
print(f"Wq is: {w_query}")

w_key = np.array([
    [0, 0, 1],
    [1, 1, 0],
    [0, 1, 0],
    [1, 1, 0]
])
print(f"Wk is :{w_key}")

w_value = np.array([
    [0, 2, 0],
    [0, 3, 0],
    [1, 0, 3],
    [1, 1, 0]
])

print(f"Wv is :{w_value}")

增加的三个转换矩阵如下图所示：
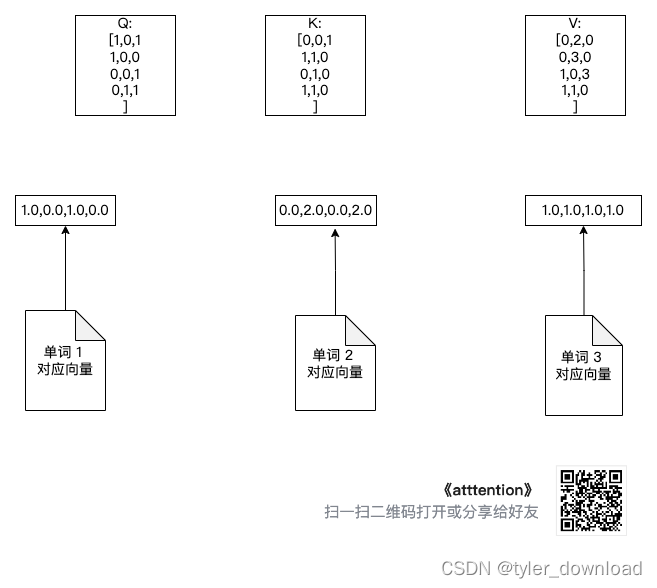
请添加图片描述

在自然语言处理中，一句话中每个单词都会分别承担 query的角色，同时每个单词都会作为 key, value 来使用，因此，我们要让每个单词都乘以 w_q，为下一步计算“和稀泥”比率做准备，因此我们执行如下操作：

print("每个向量都会作为 query 使用，因此他们都要乘以 w_query 为下一步计算分配比率做准备")
Q = np.matmul(x, w_query)
print(f"query matrix is: {Q}")

由于每个单词都要承担 key, value，所以他们还需要各自都要乘以矩阵 w_k, w_v，代码如下：

print("每个向量都会作为 key 使用，因此他们也需要乘以 w_key")
K = np.matmul(x, w_key)
print(f"key matrix is : {K}")

print("每个向量都会作为 value 使用，因此也需要乘以 w_value")
V = np.matmul(x, w_value)
print(f"value matrix is {V}")

上面计算流程如下图所示：
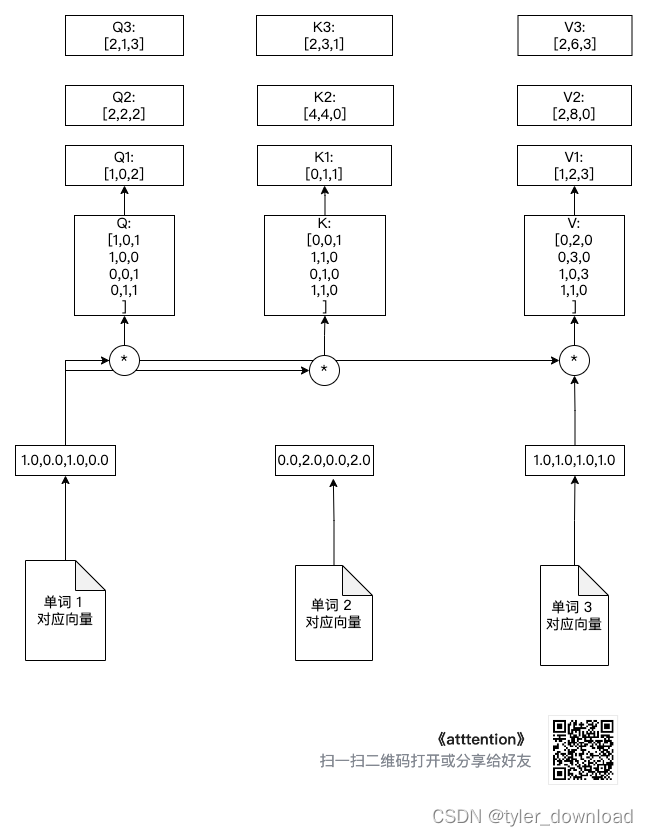
请添加图片描述

从上图可以看出，单词向量 1 分别和矩阵 Q, K, V 相乘后得到 Q1,K1,V1,同理单词向量 2 与 Q,K,V 相乘后得到Q2, K2, V2，单词向量 3 跟 Q,K,V 相乘后得到 Q3,K3,V3，为了防止线条太乱，上图我没有让单词向量 2 和单词向量 3 跟 3 个乘法操作符号相连，但我们需要知道 Q2,K2,V2,Q3,K3,V3 的来源是单词向量 2 和向量 3 做了相同操作的结果。

下面我们计算“分配比率”，它的计算方法如下：
$softmat(Q * K^T / sqrt(d_k))$
d_k 取值对应句子中单词个数，因此取值 3，它的开方是 1.75，我们取整就是 1，于是分配比率的计算如下：

from scipy.special import softmax
print(f"计算分配比率")
'''
k_d 对应 Q * K^t 后矩阵的维度，由于 Q的列数和 K^t 都是 3*3 矩阵，相乘后矩阵
每行的列数为 3，因此 k_d = sqrt(t) 就约等于 1
'''
k_d = 1
attention_scores = Q @ K.transpose() / k_d
print(attention_scores)

注意这里的 Q @ K.transpose(), 这里我们其实是把 Q1, Q2, Q3 分别与(K1, K2, K3)相乘从而得到针对每个向量的和稀泥比例。例如针对第一个单词向量的和稀泥比例就是(Q1 * K1^t, Q2 * K2 ^2, Q3 * K3 ^t), 这里 K1 ^ t 标书对向量 K1 的转置，也就是将它从行向量转为列向量，这样两个向量才能相乘。

我们看看做完上面操作后，每个向量对应的和稀泥比例，如下图所示：
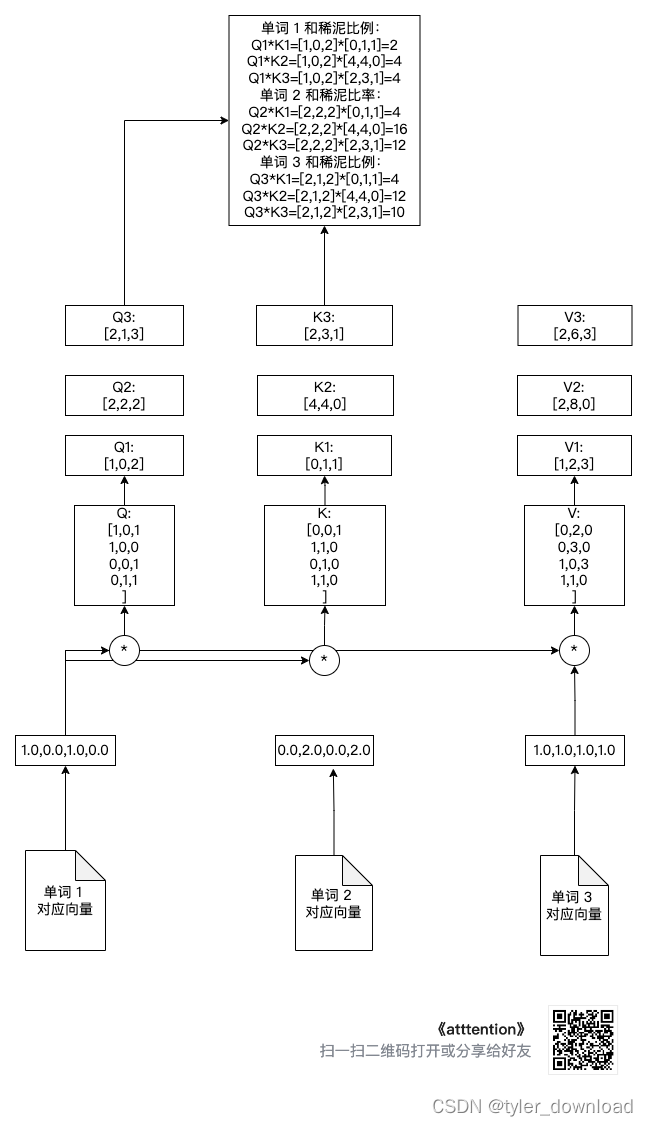
请添加图片描述
接下来我们对每个单词获得的分配比例做 softmax 正规化处理，也就是让比例加总的结果为 1，相关代码如下：

print("通过 softmax 将分配比率正规化，也就是使得各比率之和为 1")
attention_scores[0] = softmax(attention_scores[0])
attention_scores[1] = softmax(attention_scores[1])
attention_scores[2] = softmax(attention_scores[2])
#第一个单词对应的 value 分配比率
print(attention_scores[0])
#第二个单词对应的 value 分配比率
print(attention_scores[1])
#第三个单词对应的 value 分配比率
print(attention_scores[2])

上面操作对应下图：
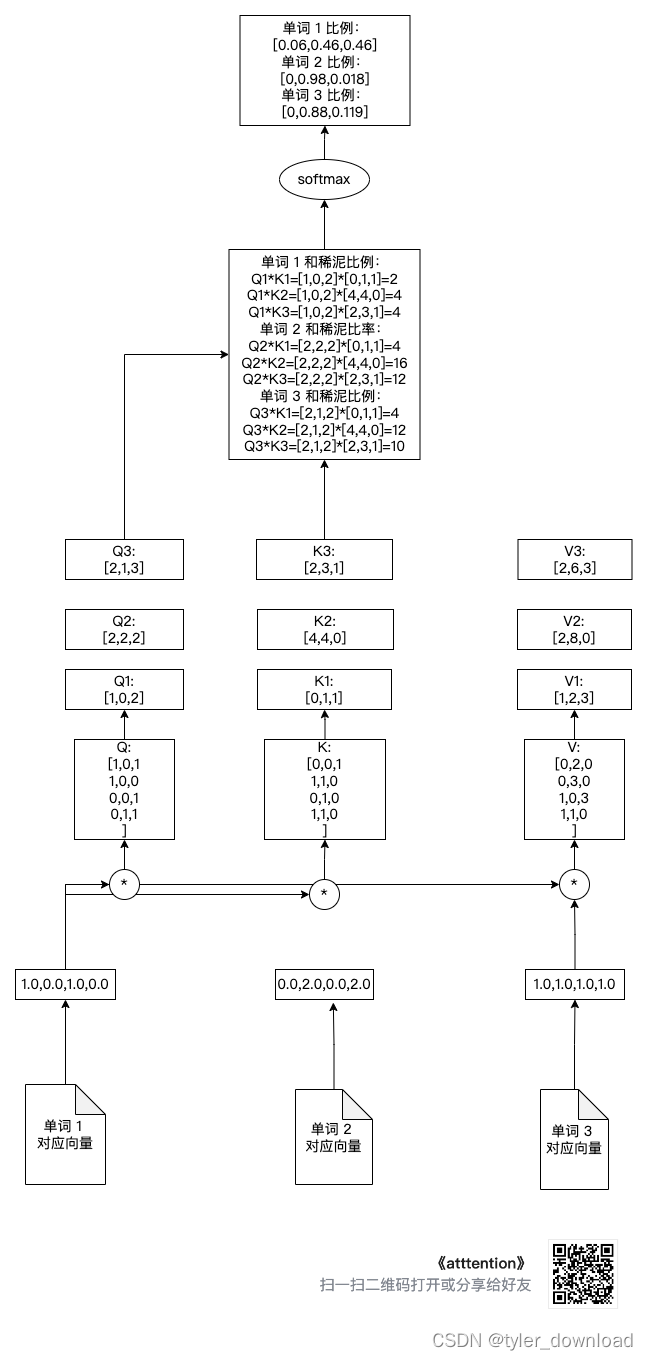
请添加图片描述
最后我们将分配比例与 V[0],V[1],V[2]相乘，然后加总就能得到其对应结果向量，下面我们就针对单词 1 做相应操作，其他单词的操作完全一样：

print("计算和稀泥结果")
print(V[0])
print(V[1])
print(V[2])

'''
计算第二，第三个单词分配比率时，只要把 attention_scores[0][i](i=1,2,3)换成
attention_scores[1][i], attention_scores[2][i]即可
'''

attention1 = attention_scores[0].reshape(-1, 1)
print(f"第一个单词的和稀泥分配比为：{attention1}")

print("第一个向量和稀泥给第一个单词的数量为:")
attention1 = attention_scores[0][0] * V[0]
print(attention1)

print("第二个向量和稀泥给第一个单词的数量为:")
attention2 = attention_scores[0][1] * V[1]
print(attention2)
print("第三个向量和稀泥给第一个单词的数量为")
attention3 = attention_scores[0][2] * V[2]
print(attention3)

print("将上面 3 个 attention 加总就是针对第一个单词和稀泥的结果")
attention_input1 = attention1 + attention2 + attention3
print(f"第一个单词的和稀泥结果：{attention_input1}")

上面操作对应如下图：
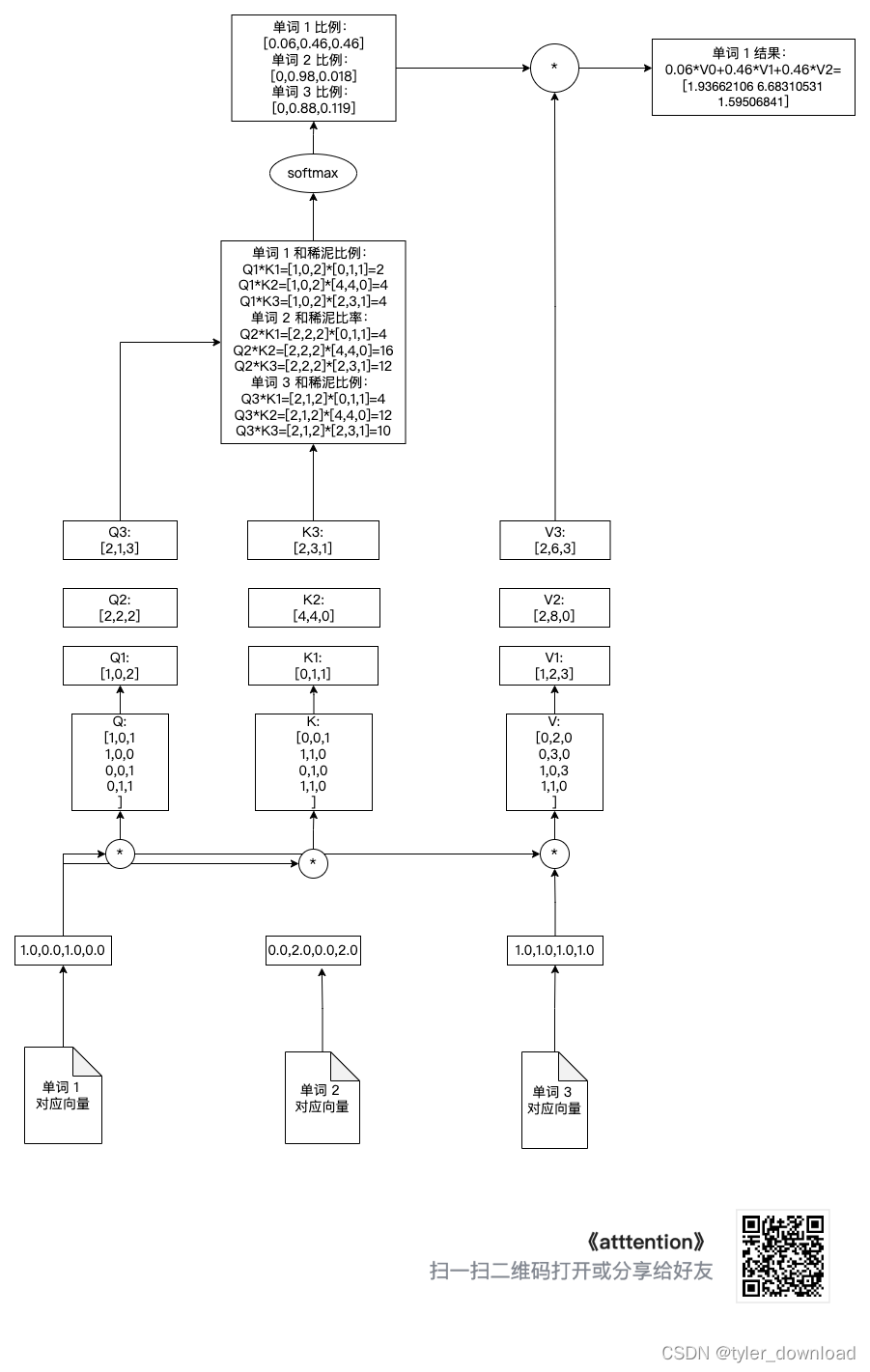
请添加图片描述
在上面运算过程中矩阵 Q,K,V 是网络要训练的参数。以上就是 self-attention 机制的基本流程。在 chatGPT 所使用的模型中，attetion 机制与上面稍微有些区别，它叫 multihead-attention，也就是将上面的过程分成 8 个并行的流程同时推进。

在我们的模拟中，单词向量的长度只有 4，而在 chatGPT 的应用中长度至少有 512, chatGPT3.5 之后长度肯定会更长，但算法流程差不多。我们就假设单词向量对应长度为 512，所谓 multihead 是指将长度为 512 的单词向量分成 8 个子向量，每个向量长度为 64，然后每个子向量都执行上面描述的操作，并且这 8 个子向量能通过并发的方式来同时执行上面的流程。

我们也模拟一下 multihead 的流程，假设 8 个长度为 64 的子向量完成上面描述的操作后，所得结果如下：

import numpy as np 

print("模拟 8 个长度为 64 的子向量完成 attention 操作后的结果，这里我们设定 Q,K,V 对应的列都是 64，因此操作结果得到的就是长度为 64 的向量")
head1 = np.random.random((3, 64))
head2 = np.random.random((3, 64))
head3 = np.random.random((3, 64))
head4 = np.random.random((3, 64))
head5 = np.random.random((3, 64))
head6 = np.random.random((3, 64))
head7 = np.random.random((3, 64))
head8 = np.random.random((3, 64))

print("将 8 个 3*64 向量在水平方向拼接变成 3*512 向量")
output_attention = np.hstack((head1, head2, head3, head4, head5, head6, head7, head8))
print(output_attention)

上面代码模拟了 8 个子向量经过前面描述流程后所得结果，然后再将 8 个364的结果横向拼接成 3512 的矩阵，根据前面我们描述的 transformer 架构，接下来就要对这个结果进行正规化处理：
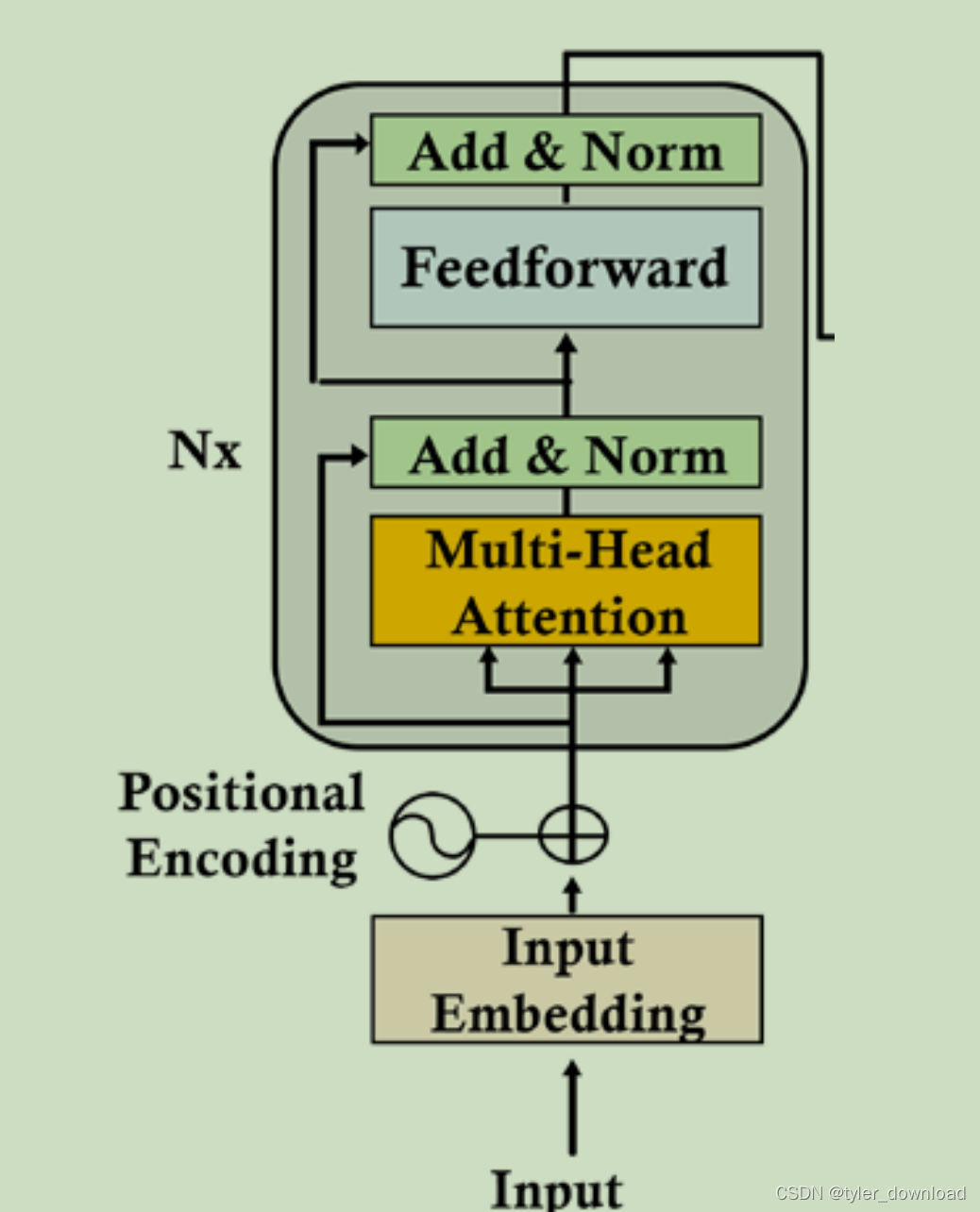
请添加图片描述

上图中multi-Head Attention 就是我们前面描述的结果，我们看看 Add & Norm 做的是什么。它其实执行了一个名为 LayerNomalization 的函数，这个函数的计算过程如下：
LayerNormalization(v) = r * (v - u)/a + b
这里 r, u, a, b 是可以计算的参数，这里 v 是函数的输入数据，它对应一个向量。如果输入v对应向量的长度是d，也就是 v 有 d 个参数 v=(v1, v2, …vd)，那么 u = (v1 + v2 +… + vd)/d, a 是输入向量 v 的标准方差 a = sqrt((v1-u) ^ 2 + …(vd-u)^2)，最后 b 是一个维度跟 v 一样的向量，这个 b 也是一个可以被网络训练的参数向量。

需要注意的是"Add & Norm"层接收了两处输入，一处是输入给 multi-head attention 层的输入向量，也就是我们把单词向量加上位置向量后的结果，一处是 multi-head attention 输出的结果，这是因为输入的单词向量警告 multi-head attention 这层后，单词向量中的某些信息可能会丢失，于是将单词向量更 multi-head attention 的结果加起来就可以确保原理包含在单词向量中的信息不丢失，这个想加操作就是"Add & Norm"中的"Add"。

继续往上是 Feedforward (FFN)层，其实就是一个简单的两层前向网络，第一层含有 2048 个节点，第二层含有 512 个节点，激活函数采用的是 ReLU，它要求的输入向量长度为 512，输出的向量也是 512，它对应的计算为：
FFN(x) = max(O, x * W1 + b1) * W2 + b2
W1 是第一层与输入层之间的连接参数，W2 是第一层与第二层的连接参数。

以上是我们对 transformer 模型的简单介绍。还有很多重要细节不好通过文字来描述，后面我们使用 transformer 架构来创建两个语言翻译模型，通过拳拳到肉的实战，或许我们才能对理论有进一步的了解，更多信息请在 B 站搜索 coding 迪斯尼。