直线的扫描转换:
DDA算法:
推理:
在计算机显示图形时,由于显示计算机的分辨率是有限的所以我们在绘制图形时需要将图形从连续量转换成离散量才能完成图形的绘制,直线的扫描转换就是将连续量转换为离散量的过程。
对于任意给我们两点
(
x
0
,
y
0
)
(x_0, y_0)
(x0,y0)与
(
x
1
,
y
1
)
(x_1, y_1)
(x1,y1)我们可以得到小面的一些量:
k
=
y
1
−
y
0
x
1
−
x
0
k = \frac{y_1-y_0}{x_1-x_0}
k=x1−x0y1−y0
此值的意义表示的是在x轴上自增1,在y轴上的增量。如图所示:
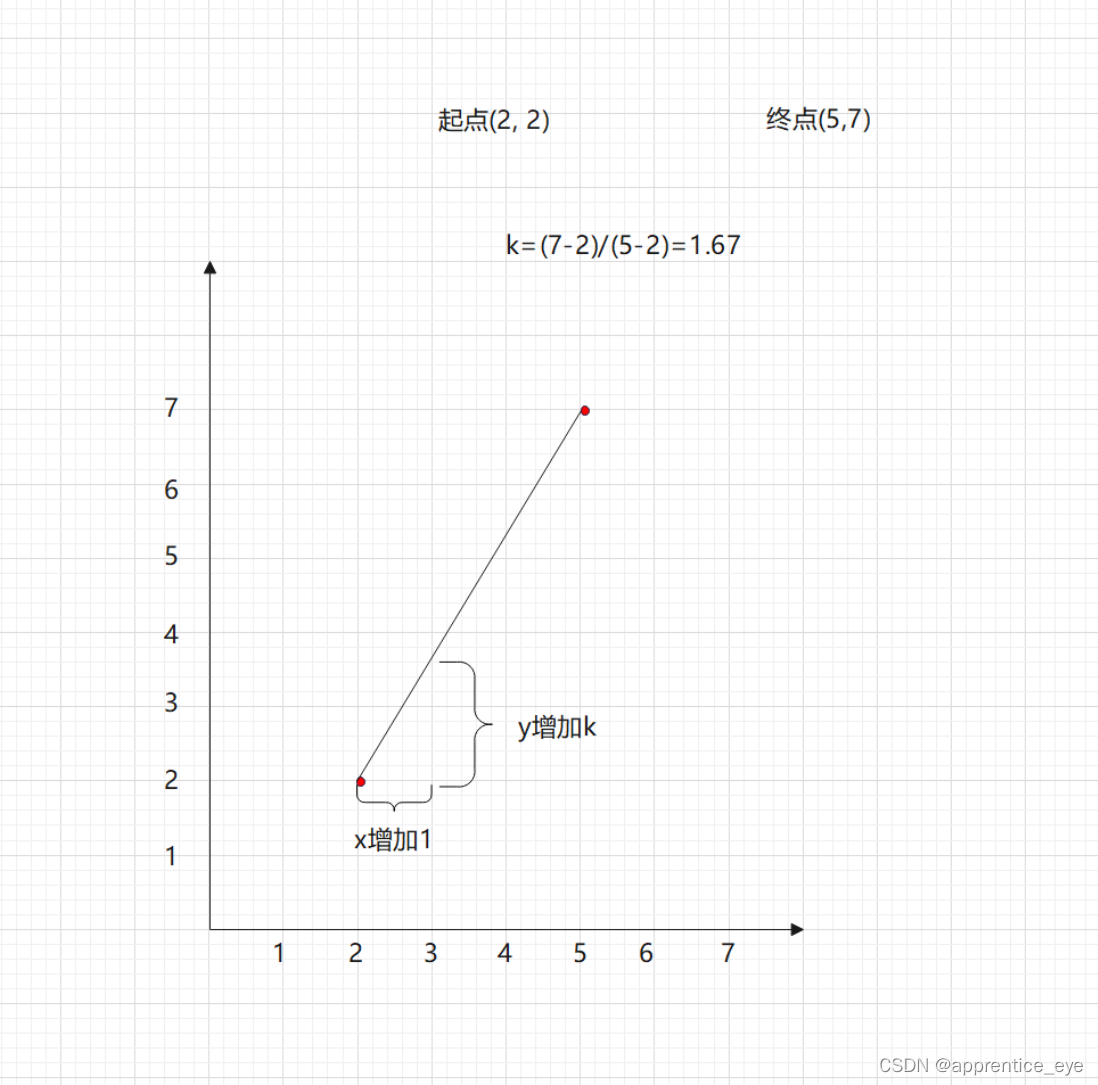
这样我们得到斜率之后,我们就知道在x轴上增加1,y轴上的增量了,但是目前我们仍旧不知道该怎么将这个这两点所确定的直线转换为离散的点集。
我们将这个图形转化为下图看一下:
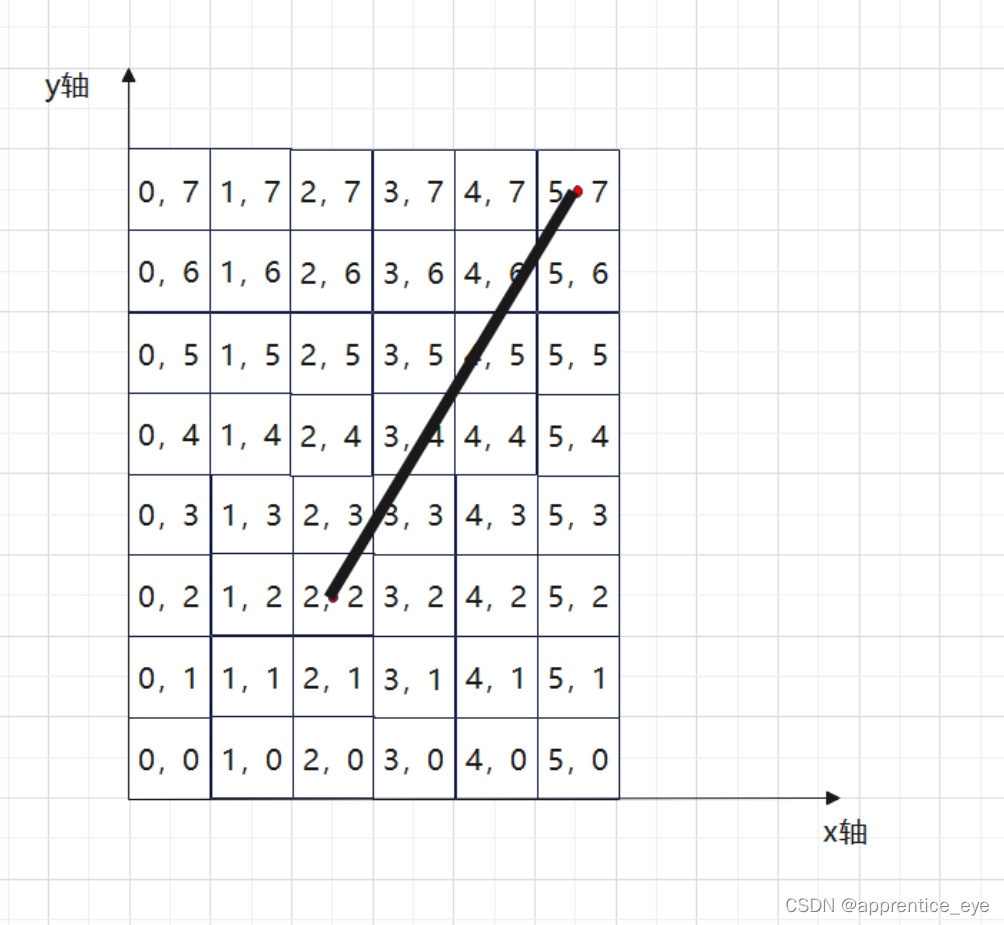
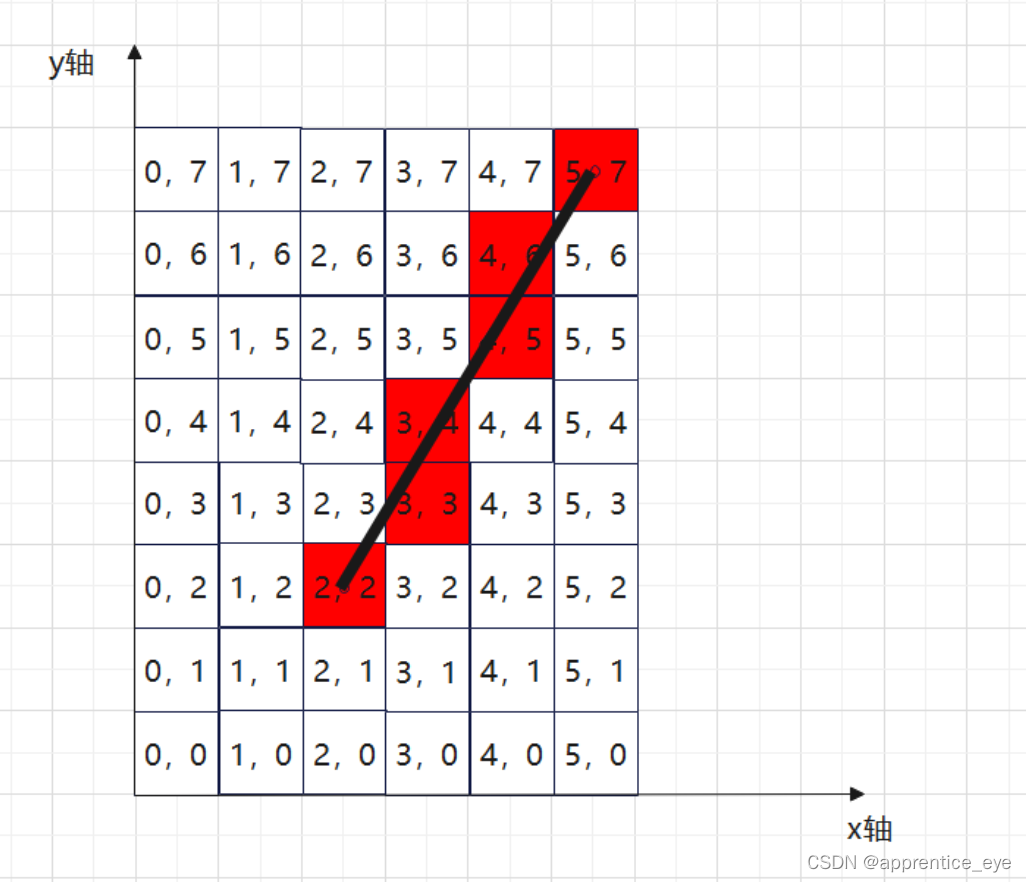
也就是说对于直线上一点我们可以使用最接近这一点的像素来表示这一点。
所以我们就可以就可以将直线转换为一个一个离散的点了,为了获取最多的能够表示这一条直线的点,对于斜率为k的直线,我们需要沿着增量最快的轴作为自变量来增加,因为像素是一个挨着一个,所以作为自变量的轴每一次增加1,因为k的取值可以变化,无论k值怎样变化,第一次决策的点都应该属于下面的八个点,这样我们么一次抉择下一个点就是在周围的八个点之间做一个决策:
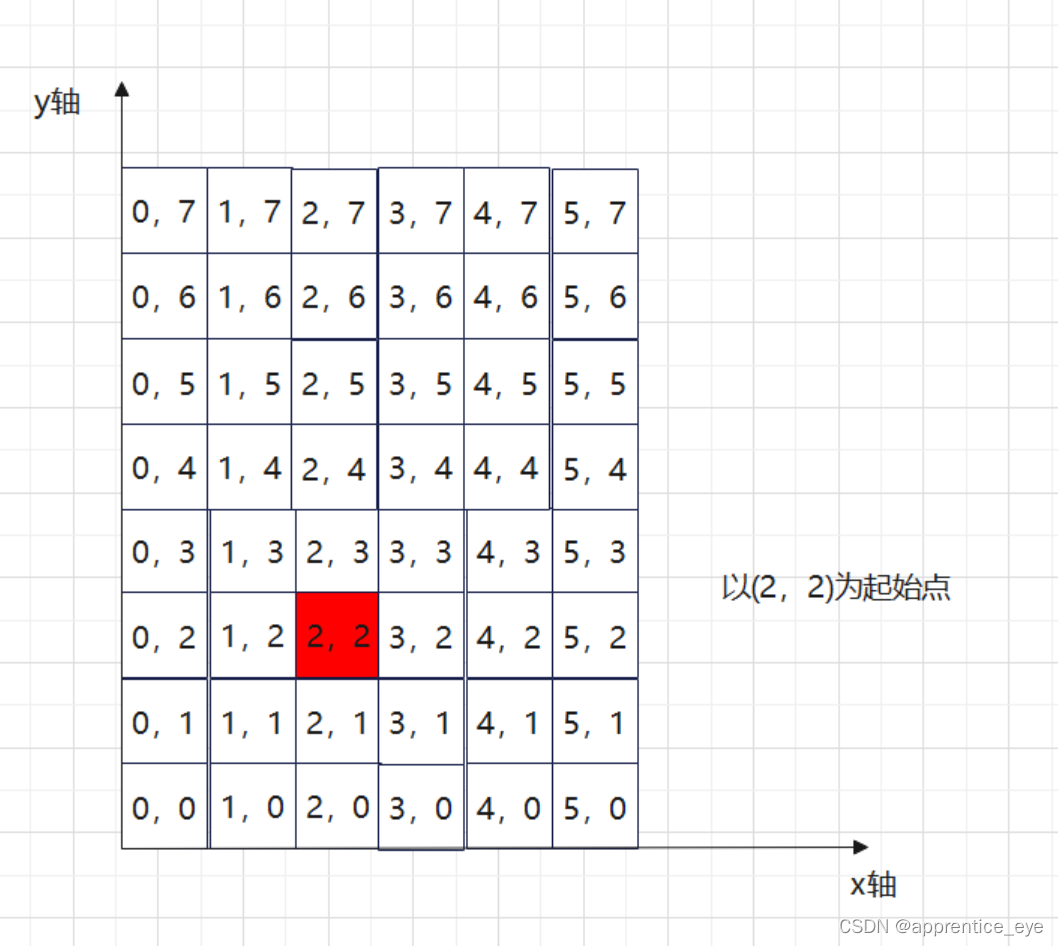
当k选择一个具体的值之后如k=0.5则直线的下一次取点的决策范围应该为:
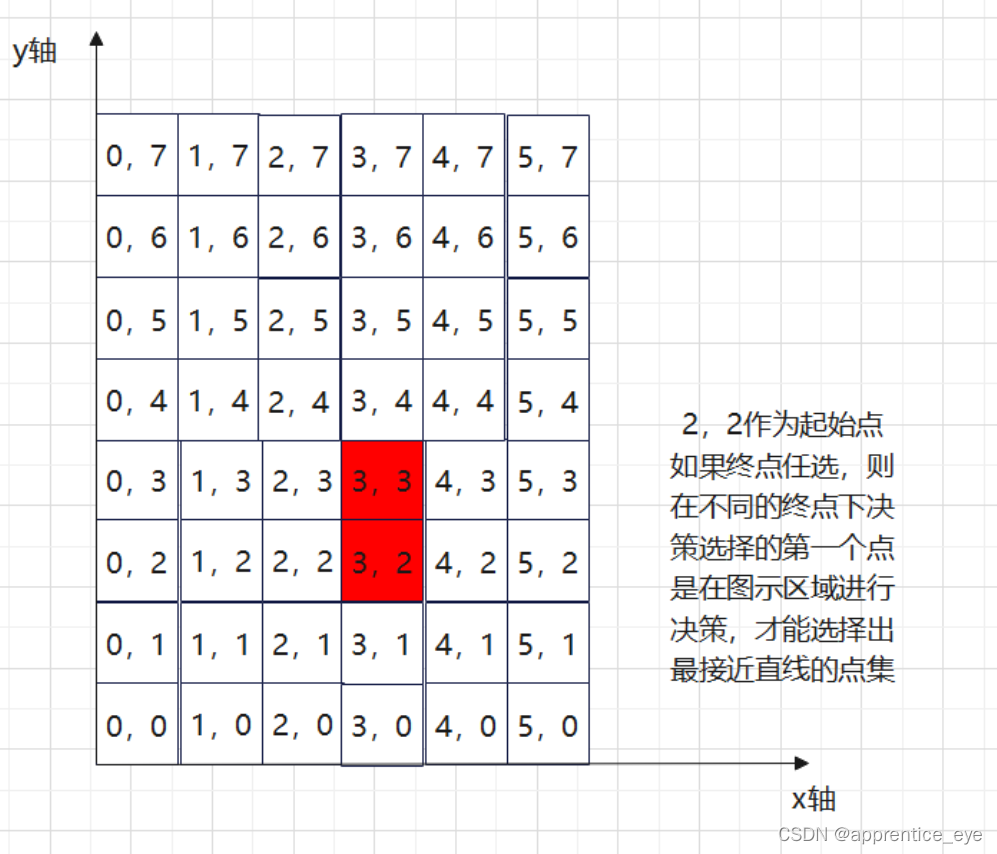
现在我们已经说明了为什么要选择增量最快的轴作为自变量轴,同时也说明了为什么作为自变量的轴每一次要增加1而不是增加2或者其他的数字。
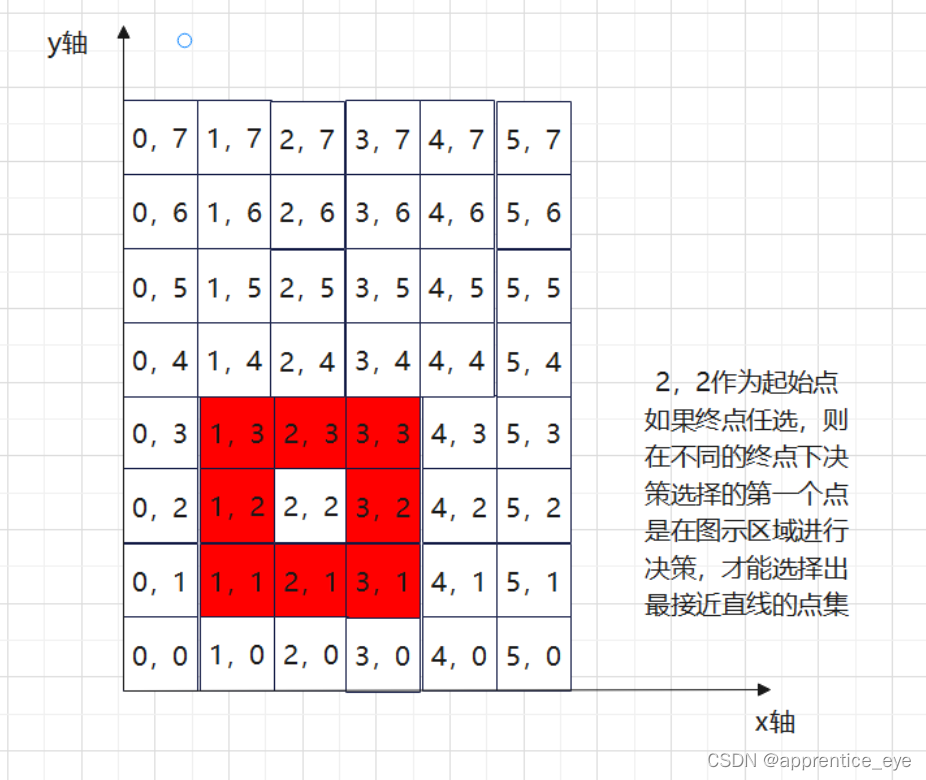
如果不使用增量最快的轴作为自变量轴则会出现什么情况能。如起始点(2,2),斜率为k的直线选择变化慢的轴作为自变量,则决策范围为:
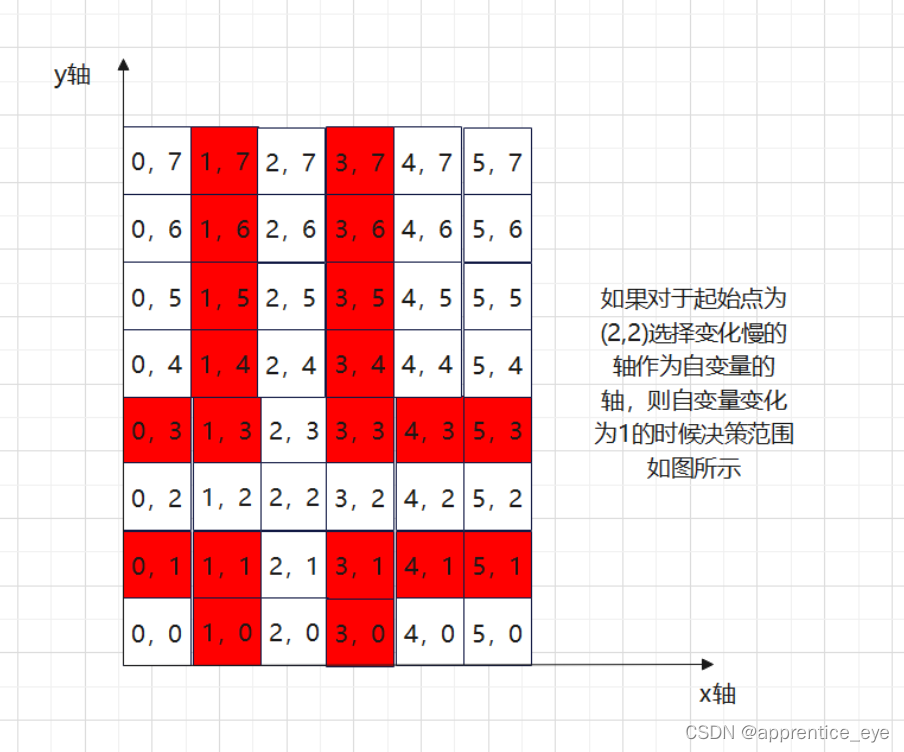
可以看出这种取法会导致我们选取的点不是最符合直线的点。
所以我们要采取自变量变化快的轴作为我们的自变量,每次变化1.
如果根据起点与终点确定了点的坐标,我们同样要根据点的坐标进行舍入,来确定整数坐标的像素作为表是直线的点,如何进行舍入呢,我们以(2,2)点表示的像素为例,我们只需要确定(x,y)是不是属于红色区域的点
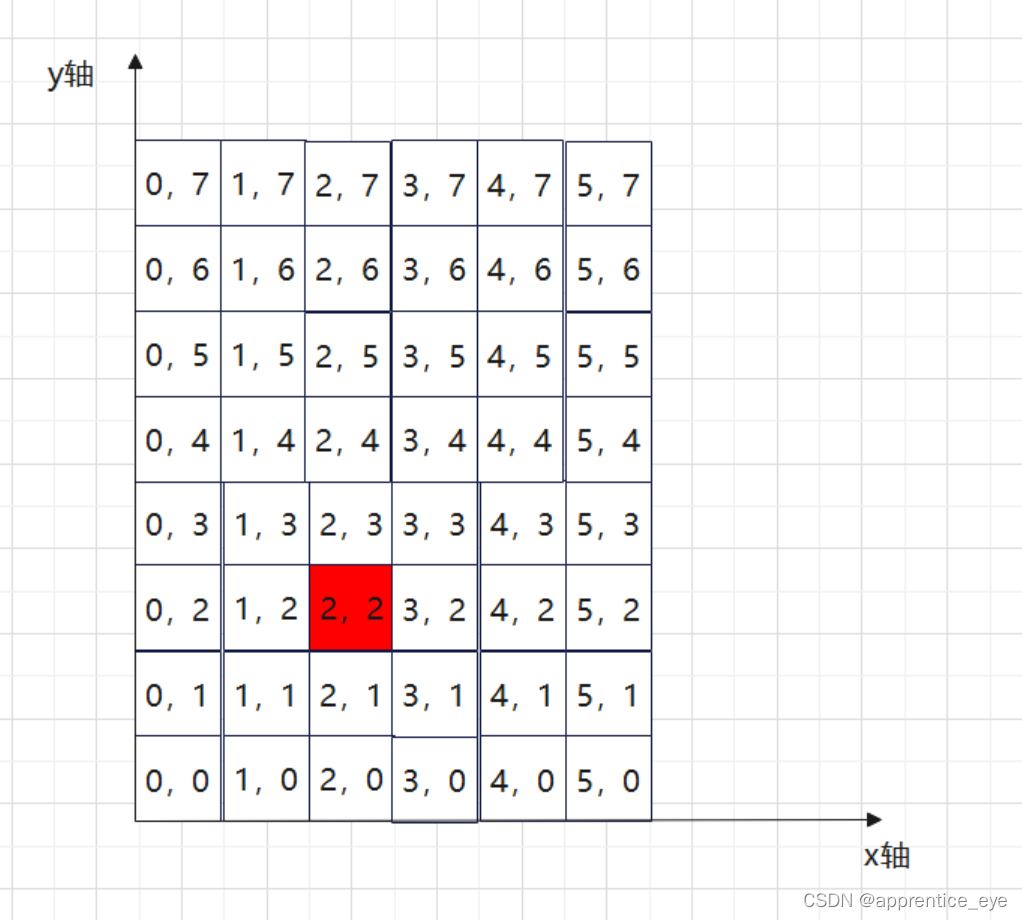
公式为:
1.5
<
=
x
<
2.5
→
x
=
2
1.5
<
=
y
<
2.5
→
y
=
2
1.5<=x<2.5\rightarrow x = 2\\ 1.5<=y<2.5\rightarrow y = 2
1.5<=x<2.5→x=21.5<=y<2.5→y=2
因为c语言中的取整规则是向下取整,所以我们在确定
点的时候要将x,y分别加上0.5,用(x+0.5, y+0.5)取整来确定像素点。
公式推导
起点
(
x
起
,
y
起
)
终点
(
x
终
,
y
终
)
k
=
y
终
−
y
起
x
终
−
x
起
Δ
x
=
x
终
−
x
起
Δ
y
=
y
终
−
y
起
k
=
Δ
y
Δ
x
如果
0
≤
k
≤
1
则说明
x
轴变化快,选择
x
作为自变量
起始点
(
x
起
,
y
起
)
:
x
1
=
x
起
+
1
y
1
=
y
起
+
k
选取点的时候选取:
(
⌊
x
1
+
0.5
⌋
,
⌊
y
1
+
0.5
⌋
)
x
2
=
x
1
+
1
y
2
=
y
1
+
k
选取点的时候选取:
(
⌊
x
2
+
0.5
⌋
,
⌊
y
2
+
0.5
⌋
)
.
.
.
.
.
.
起点(x_起, y_起)终点(x_终, y_终)\\ k = \frac{y_终-y_起}{x_终-x_起}\\ \Delta x = x_终- x_起\\ \Delta y = y_终-y_起\\ k = \frac{\Delta y}{\Delta x}\\ 如果0\leq k\leq1则说明x轴变化快,选择x作为自变量\\ 起始点(x_起, y_起):\\ x_1 = x_起 + 1\\ y_1 = y_起 + k\\ 选取点的时候选取:(\lfloor x_1+0.5\rfloor, \lfloor y_1+0.5\rfloor)\\ x_2 = x_1 + 1\\ y_2 = y_1 + k\\ 选取点的时候选取:(\lfloor x_2+0.5\rfloor, \lfloor y_2+0.5\rfloor)\\ ......
起点(x起,y起)终点(x终,y终)k=x终−x起y终−y起Δx=x终−x起Δy=y终−y起k=ΔxΔy如果0≤k≤1则说明x轴变化快,选择x作为自变量起始点(x起,y起):x1=x起+1y1=y起+k选取点的时候选取:(⌊x1+0.5⌋,⌊y1+0.5⌋)x2=x1+1y2=y1+k选取点的时候选取:(⌊x2+0.5⌋,⌊y2+0.5⌋)......
所以我们先计算k,然后一步一步的进行计算即可。
但是上述只讨论了
0
<
=
k
<
=
1
0<=k<=1
0<=k<=1这一种情况,但是这已经够用了,因为对于坐标系内任意一点都可以通过一些对称轴转化至
0
<
=
k
<
=
1
0<=k<=1
0<=k<=1区域内。
对于
k
>
1
k>1
k>1的情况,我们知道此时变化较快的轴为y轴所以选取y轴为增加1的轴,其余分析同上。
如图:
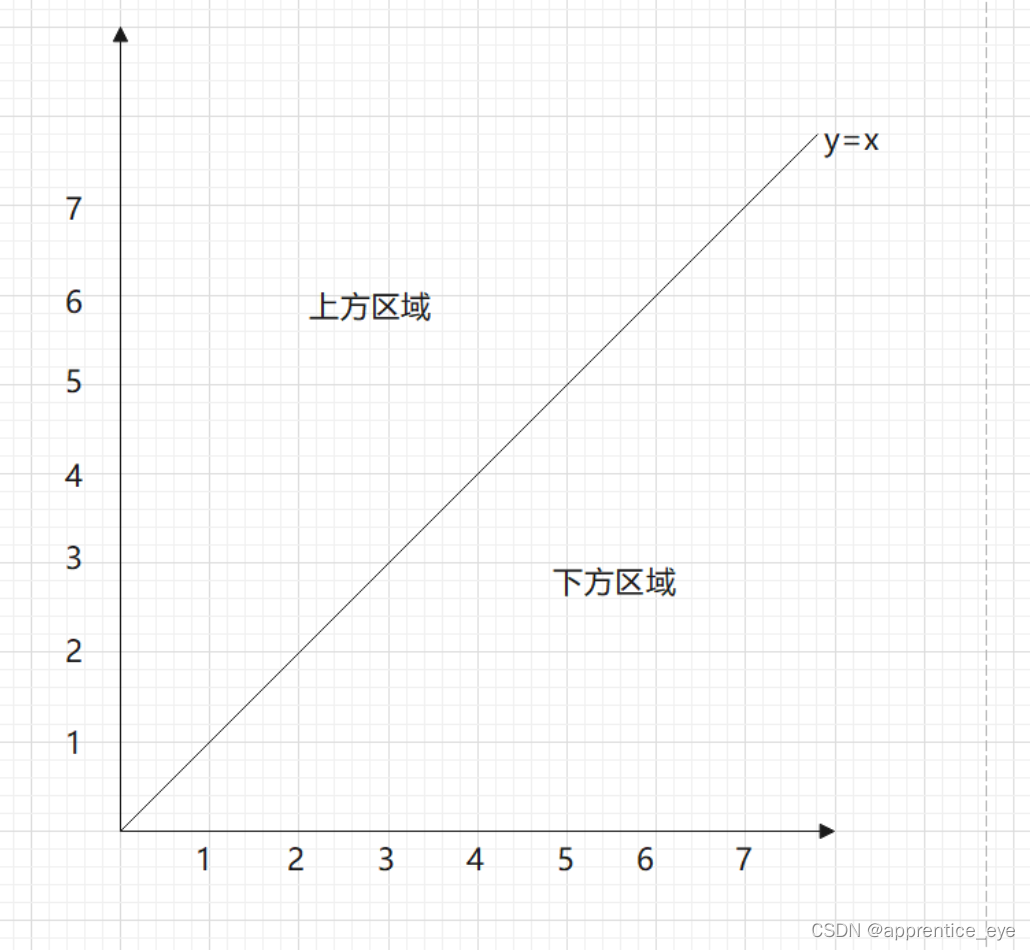
我们可以通过对称轴y=x将上方区域的点转换到下方区域。其他区域也是同理。将点进行对称时一定要按照以起点为原点进行对称,也就是说这涉及到一个坐标系变换的问题,我们根据坐标系的变换规则我们可以知道
(1)当要进行终点在起始点的左上方时:
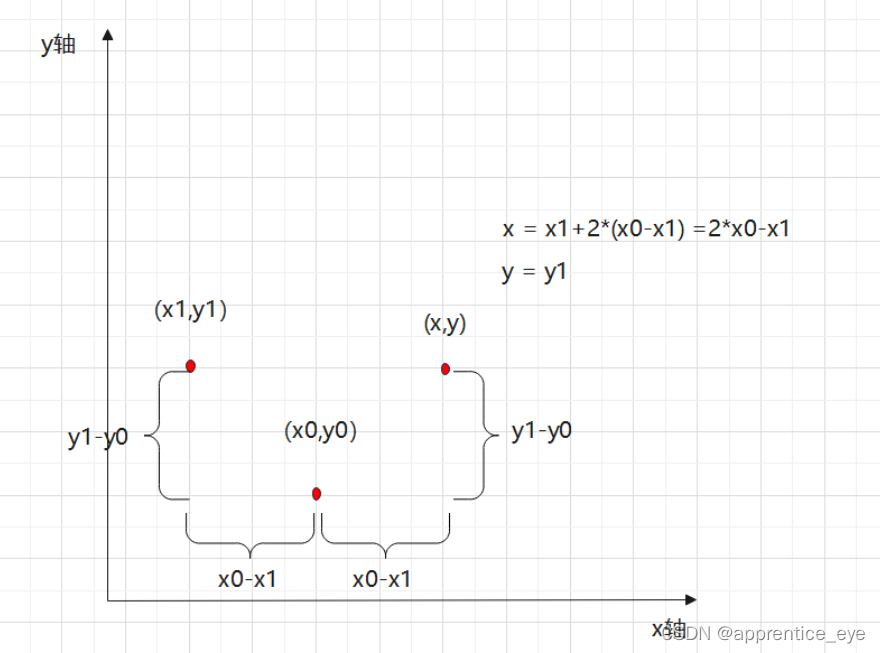
$x = x1+2*(x0-x1) =2x0-x1\
y = y1
$
其余同理可得:
(2)当终点在起始点的左下方的时候:
x
=
x
1
+
2
∗
(
x
0
−
x
1
)
=
2
∗
x
0
−
x
1
y
=
y
1
+
2
∗
(
y
0
−
y
1
)
=
2
∗
y
0
−
x
1
x = x1+2*(x0-x1) =2*x0-x1\\ y = y1 + 2*(y0-y1) = 2*y0-x1
x=x1+2∗(x0−x1)=2∗x0−x1y=y1+2∗(y0−y1)=2∗y0−x1
(3)当终点在起始点的右下方的时候:
$
x =x1\
y = y1 + 2(y0-y1) = 2*y0-x1
$
然后通过对称过去的点计算出点的坐标然后对称回来进行绘制即可。
我们可以写出下述算法:
void paintline(CPoint start, CPoint end, CDC* pDC, int deltax, int deltay, int flag ) {
int num;
float x1, y1, xIncreation, yIncreation;
CPoint point;
CPoint end2;
switch (flag) {
case 1:
end2.x = end.x;
end2.y = end.y;
break;
case 2:
end2.x = 2 * start.x - end.x;
end2.y = end.y;
break;
case 3:
end2.x = 2 * start.x - end.x;
end2.y = 2 * start.y - end.y;
break;
case 4:
end2.y = 2 * start.y - end.y;
end2.x = end.x;
break;
}
deltax = end2.x - start.x;
deltay = end2.y - start.y;
num = deltax > deltay ? deltax : deltay;
if (deltax > deltay) {
yIncreation = 1.0 * deltay / deltax;
xIncreation = 1;
}
else {
xIncreation = 1.0 * deltax / deltay;
yIncreation = 1;
}
x1 = start.x;
y1 = start.y;
for (int i = 0; i < num; i++) {
point.x = (int)(x1 + 0.5);
point.y = (int)(y1 + 0.5);
switch (flag) {
case 1:
pDC->SetPixelV(point, RGB(255, 0, 0));
break;
case 2:
point.x = 2 * start.x - point.x;
pDC->SetPixelV(point, RGB(255, 0, 0));
break;
case 3:
point.x = 2 * start.x - point.x;
point.y = 2 * start.y - point.y;
pDC->SetPixelV(point, RGB(255, 0, 0));
break;
case 4:
point.y = 2 * start.y - point.y;
pDC->SetPixelV(point, RGB(255, 0, 0));
break;
}
x1 += xIncreation;
y1 += yIncreation;
}
}
void paintLine(CPoint start, CPoint end, CDC * pDC) {
int deltax = end.x - start.x;
int deltay = end.y - start.y;
if (deltax > 0 && deltay > 0) {
paintline(start, end, pDC, deltax, deltay, 1);
}
else if (deltax < 0 && deltay>0) {
paintline(start, end, pDC, deltax, deltay, 2);
}
else if (deltax < 0 && deltay < 0) {
paintline(start, end, pDC, deltax, deltay, 3);
}
else if (deltax > 0 && deltay < 0) {
paintline(start, end, pDC, deltax, deltay, 4);
}
}
void Ctest2Dlg::OnLButtonDown(UINT nFlags, CPoint point)
{
if (!flag) {
start = point;
flag = !flag;
}
else {
end = point;
flag = !flag;
CDC* pDC = GetDC();
paintLine(start, end, pDC);
ReleaseDC(pDC);
}
CDialogEx::OnLButtonDown(nFlags, point);
}
中点画线法
算法原理
与DDA算法不同中点画线法的主要思想是这样的,对于任意一条直线来说这条直线会将平面分成上下两部分,将直线上方的点代入到直线方程中会得到大于0的结果,将直线下方的点代入直线方程中会得到小于0的结果。
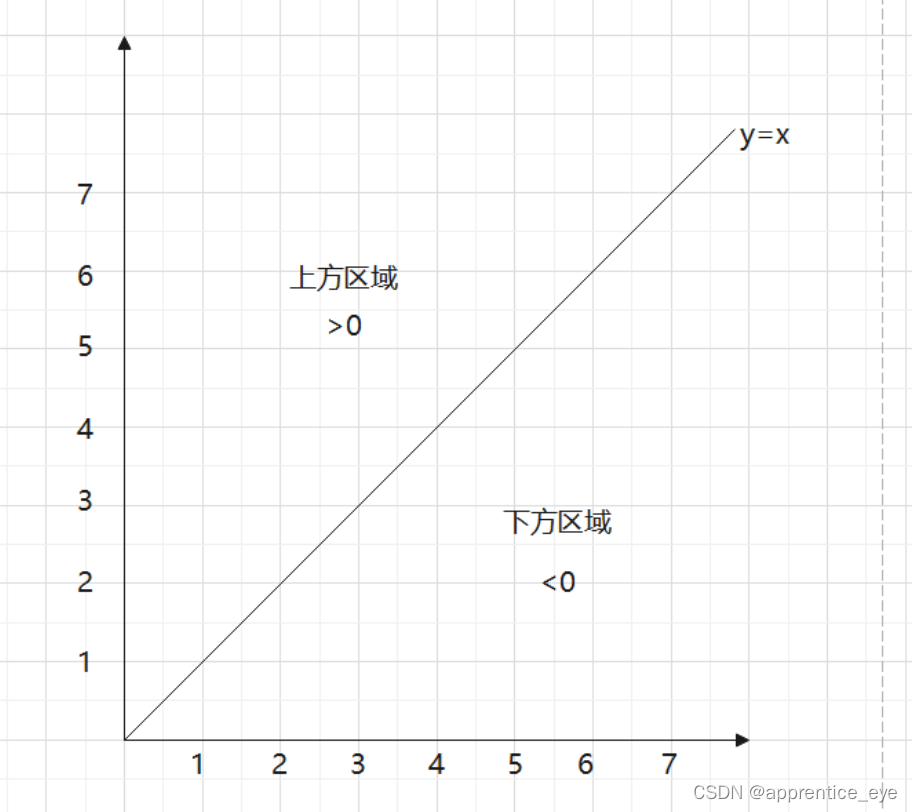
也就是说如果我们代入两个像素的中间值,会得到大于0或小于0的结果,当大于0时我们需要选取直线下方的点作为我们的选取的点,当代入小于0的时候我们需要选取上方的点作为我们选取的点。
我们先推导0<=k<=1时选取点的条件:
设方程为
y
=
k
∗
x
+
b
y = k*x+b
y=k∗x+b假设现在选取的点为
(
x
,
y
)
(x, y)
(x,y)则下一点需要在
(
x
+
1
,
y
+
0
)
(x+1, y+0)
(x+1,y+0)与
(
x
+
1
,
y
+
1
)
(x+1, y+1)
(x+1,y+1)做出选择,此时我们将
(
x
+
1
,
y
+
0.5
)
(x+1, y+0.5)
(x+1,y+0.5)代入得到
d
=
y
+
0.5
−
k
∗
(
x
+
1
)
−
b
d = y+0.5-k*(x+1)-b
d=y+0.5−k∗(x+1)−b此时d>0 或 d<0
- 当d>0时选择(x+1, y)点
下面那一点就从 ( x + 2 , y + 0 ) (x+2, y+0) (x+2,y+0)与 ( x + 2 , y + 1 ) (x+2, y+1) (x+2,y+1)之中选择,将 ( x + 2 , y + 0.5 ) (x+2, y+0.5) (x+2,y+0.5)代入,$\d_{next} = y+0.5 - k*(x+1)-b\$ d = y + 0.5 − k ∗ ( x + 2 ) − b d = y+0.5-k*(x+2)-b d=y+0.5−k∗(x+2)−b
d n e x t = d + 0.5 − k d_{next} = d+0.5-k dnext=d+0.5−k
d n e x t − d = − k d_{next} - d = -k dnext−d=−k - 当d<0时选择(x+1, y+1)点.
下面那一点就从 ( x + 2 , y + 1 ) (x+2, y+1) (x+2,y+1)与 ( x + 2 , y + 2 ) (x+2, y+2) (x+2,y+2)之中选择,将 ( x + 2 , y + 1.5 ) (x+2, y+1.5) (x+2,y+1.5)代入,$\d_{next} = y+1.5 - k*(x+1)-b\$ d = y + 0.5 − k ∗ ( x + 2 ) − b d = y+0.5-k*(x+2)-b d=y+0.5−k∗(x+2)−b
d n e x t = d + 1 − k d_{next} = d+1-k dnext=d+1−k
d n e x t − d = 1 − k d_{next} - d = 1-k dnext−d=1−k
我们知道了增量是如何变化的还不够,我们需要求出初始d的值,
d = y − k ∗ x + b d = y-k*x+b d=y−k∗x+b,因为初始点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)在直线上将点(x_0+1, y_0+0.5)代入即可求出初始d。
d = 0.5 + k;
因为k>1的情况与0<=k<=1可以通过对称得到,所以对于k>1的情况我们将所有的x换成y,所有的y换成x就能得到k>1情况下的中点画线法。
减少浮点运算
因为增量与-k或0.5-k有关,这种是可能涉及到浮点运算的,为了避免浮点运算,我们通过*2
Δ
x
\Delta x
Δx来将浮点运算转换为整数运算。
此时对于所有过程我们都要乘上2
Δ
x
\Delta x
Δx,
由此得到初始
d
=
Δ
x
−
2
∗
Δ
y
d = \Delta x - 2*\Delta y
d=Δx−2∗Δy
相应的d的增量变成
−
2
∗
Δ
y
-2*\Delta y
−2∗Δy与
2
∗
Δ
x
−
2
∗
Δ
y
2*\Delta x - 2*\Delta y
2∗Δx−2∗Δy
算法实现
算法的实现与上面DDA算法类似。
代码如下:
void paintline(CPoint start, CPoint end, CDC* pDC, int deltax, int deltay, int flag) {
int num;
int d;
CPoint point, point2;
CPoint end2;
switch (flag) {
case 1:
end2.x = end.x;
end2.y = end.y;
break;
case 2:
end2.x = 2 * start.x - end.x;
end2.y = end.y;
break;
case 3:
end2.x = 2 * start.x - end.x;
end2.y = 2 * start.y - end.y;
break;
case 4:
end2.y = 2 * start.y - end.y;
end2.x = end.x;
break;
}
deltax = end2.x - start.x;
deltay = end2.y - start.y;
num = deltax > deltay ? deltax : deltay;
if (deltax >= deltay) {
d = deltax - 2 * deltay;
}
else {
d = deltay - 2 * deltax;
}
point.x = start.x;
point.y = start.y;
for (int i = 0; i < num; i++) {
switch (flag) {
case 1:
point2.x = point.x;
point2.y = point.y;
pDC->SetPixelV(point2, RGB(255, 0, 0));
break;
case 2:
point2.x = 2 * start.x - point.x;
point2.y = point.y;
pDC->SetPixelV(point2, RGB(255, 0, 0));
break;
case 3:
point2.x = 2 * start.x - point.x;
point2.y = 2 * start.y - point.y;
pDC->SetPixelV(point2, RGB(255, 0, 0));
break;
case 4:
point2.y = 2 * start.y - point.y;
point2.x = point.x;
pDC->SetPixelV(point2, RGB(255, 0, 0));
break;
}
if (d > 0) {
if (deltax >= deltay) {
point.x += 1;
d = d - 2 * deltay;
}
else {
point.y += 1;
d = d - 2 * deltax;
}
}
else {
point.x += 1;
point.y += 1;
if (deltax >= deltay) {
d = d + (2 * deltax - 2 * deltay);
}
else {
d = d + (2 * deltay - 2 * deltax);
}
}
}
}
void paintLine(CPoint start, CPoint end, CDC* pDC) {
int deltax = end.x - start.x;
int deltay = end.y - start.y;
if (deltax > 0 && deltay > 0) {
paintline(start, end, pDC, deltax, deltay, 1);
}
else if (deltax < 0 && deltay>0) {
paintline(start, end, pDC, deltax, deltay, 2);
}
else if (deltax < 0 && deltay < 0) {
paintline(start, end, pDC, deltax, deltay, 3);
}
else if (deltax > 0 && deltay < 0) {
paintline(start, end, pDC, deltax, deltay, 4);
}
}
这些代码都可以进行一下优化,这样能够提高效率,大家可以自行去优化。