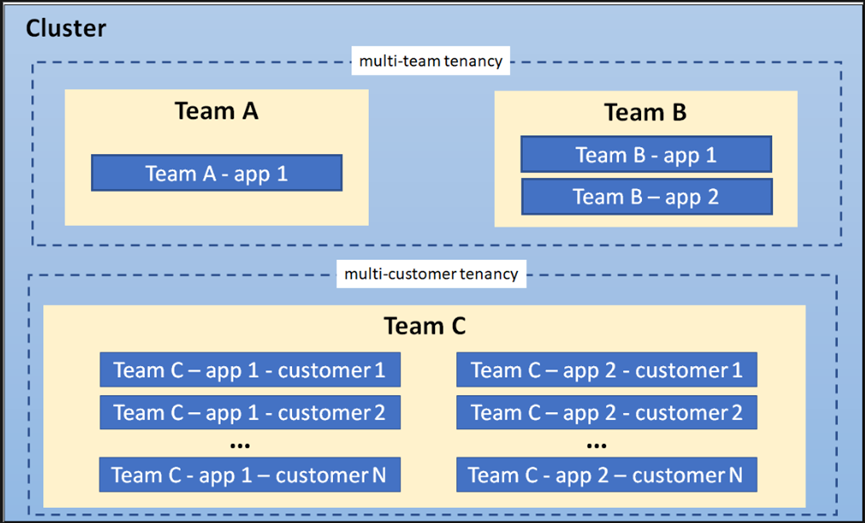
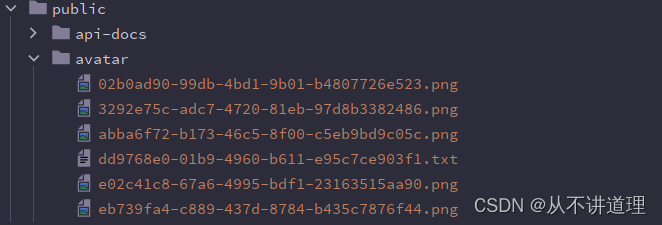
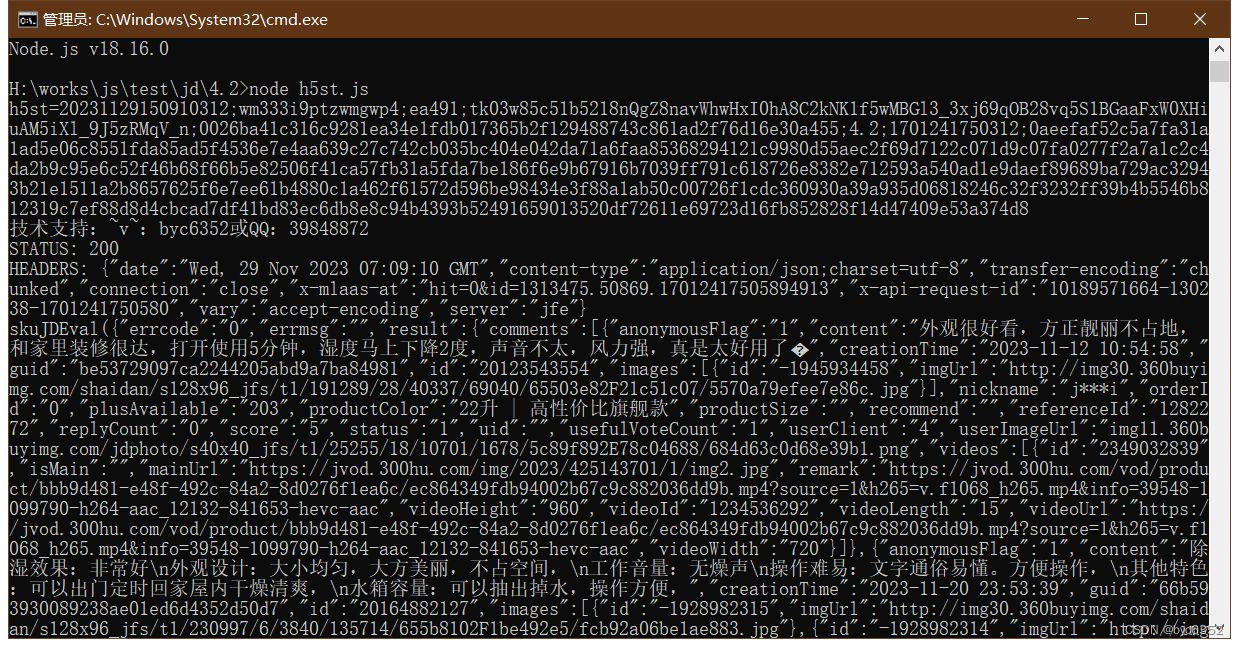
或
(1)
(2)
欧拉公式
(3)
设(3)有特解
是(1)的特解
是(2)的特解
例 :
解
所以其通解为
这是属于上一篇提到的第一种情况
其特解
即
简化
-2a=1
a=-1/2
原方程特解为
原方程通解为
解法二
将 或
改写为
设是特征方程的k重根(k=0或1)
则方程特解形如:
其中 m= max{n,l} ,指多项式的幂。
用解法二重求例题
解
解
所以其通解为
i不是特征方程的根,k=0
设为特解
所以代入原式
-acosx-bsinx-acosx-bsinx=sinx
-2acosx-(2b+1)sinx=0
因为常数
所以线性无关。
所以 -2a=-(2b+1)=0
a=0,b=-1/2
例
可以利用叠加原理,分别求特解。
1、先求齐次线性微分方程的通解
通解为
将右边的自由项,拆解成两部分。
的特解
的特解
所以所求方程为
高阶方程的求解
例
,
的通解
不是特征方程的根。
可设特解为
代入原方程
a=1/8