离散系统的频域分析(数字信号处理实验2-1)

news2024/11/25 16:02:53

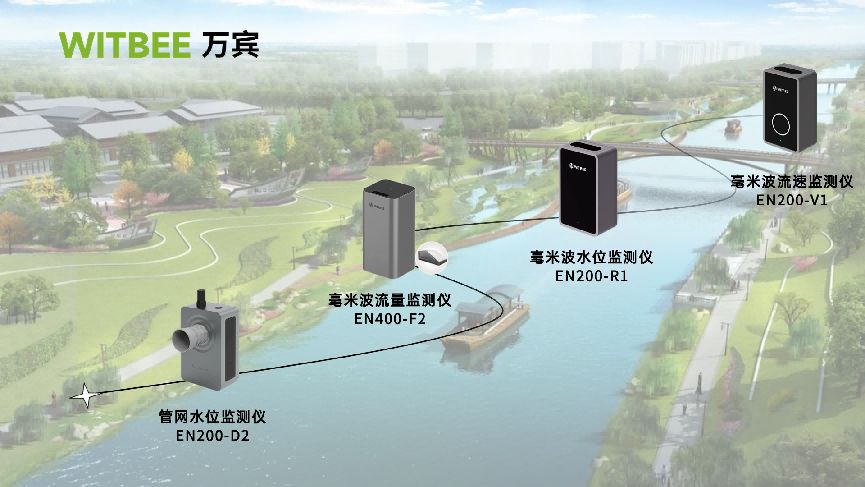
创建具有15 Hz和40 Hz分量频率的信号，叠加两个信号形成混合信号x，使用fft命令绘制x的频域图，标注频率为横坐标，平均能量为纵坐标。

文章目录

一.题目
二.实验目的
三.实验仪器
四.实验原理
- - 1.MATLAB使用函数
  - 2.离散傅里叶变换(DFT)实验原理
五.实验步骤
六.实验代码与实验现象
- 1.完整代码
- 2.代码解析
七.实验结论及分析
八.Matlab实验源文件

一.题目

创建具有15 Hz和40 Hz分量频率的信号，叠加两个信号形成混合信号x，使用fft命令绘制x的频域图，标注频率为横坐标，平均能量为纵坐标。

二.实验目的

（1）掌握求离散信号频谱的方法。
（2）掌握求频域离散系统的频率响应特性。
（3）比较男女生的频谱特点

三.实验仪器

计算机，MATLAB软件

四.实验原理

1.MATLAB使用函数

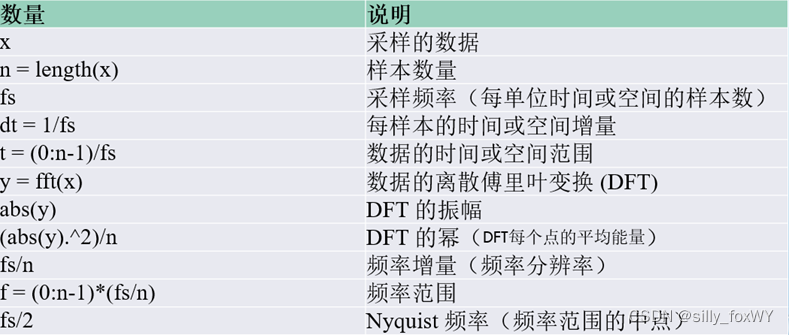
在这里插入图片描述

2.离散傅里叶变换(DFT)实验原理

在信号的时域表示形式和频域表示形式之间，一个域的周期性对应于另一个域的离散性，一个域的非周期性对应于另一个域的连续性。所以，周期的离散时间信号的频谱是离散频率的周期函数。当信号在时域和频域中都是抽样的离散函数时，按照傅里叶变换的概念，他们在两个域中也必然是周期的。但是，用计算机去完成这样无限长序列的运算，显然是不可能的。同时由于这些序列的周期性，他们的信息均包含在一个周期之中，因此也没有必要作无限长序列的运算。这样，就有必要从时域和频域都缩减到一个限定的范围内来进行。这个范围，就是时间函数的一个周期Tp 和频谱函数的一个周期Ωp 。把离散信号在时域和频域的函数中各取一周期，并定义他们是离散傅里叶变换对，如以 DFT 表示离散傅里叶正变换，IDFT 表示离散傅里叶反变换，则有X (k ) = DFT[x(n)]，x(n) = IDFT[ X (k )]
由此可见，离散傅里叶变换已经不是通常意义的傅里叶变换了。这种变换的特点，是信号在频域和时域中都只取有限个离散数据，只有当这些数据按一定的周期分别构成周期性的离散时间函数和周期性得离散频率函数时，他们才成为通常意义的傅里叶变换对。
计算离散傅里叶变换，既由 x(n) 计算 X (k ) 。有了周期的离散信号 ~x (n) 的频谱函数 ~X（k），按定义，只要取一个周期 X (k ) ，它就是 ~x (n) 一个周期 x(n) 的离散傅里叶变换。
对非周期离散信号的频谱进行抽烟可得X(k)
在这里插入图片描述
根据离散傅里叶变换的定义，取频谱函数的一个周期，于是得：

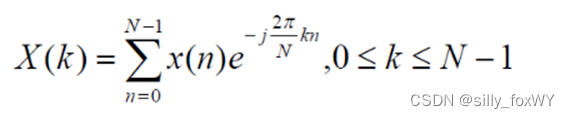
X(k)就称为x(n)的离散傅里叶变换DFT。k从0到N-1之间每取一个整数值，即可算出频谱函数的一个样点，总共有N个样点。

五.实验步骤

离散系统的频域分析

创建具有 15 Hz 和 40 Hz 分量频率的信号，叠加两个信号形成混合信号x, 使用fft命令绘制x的频域图，标注频率为横坐标，平均能量为纵坐标。
用sin函数创建频率信号；使用fftshift函数执行以横坐标0为中心的循环移位。

六.实验代码与实验现象

1.完整代码

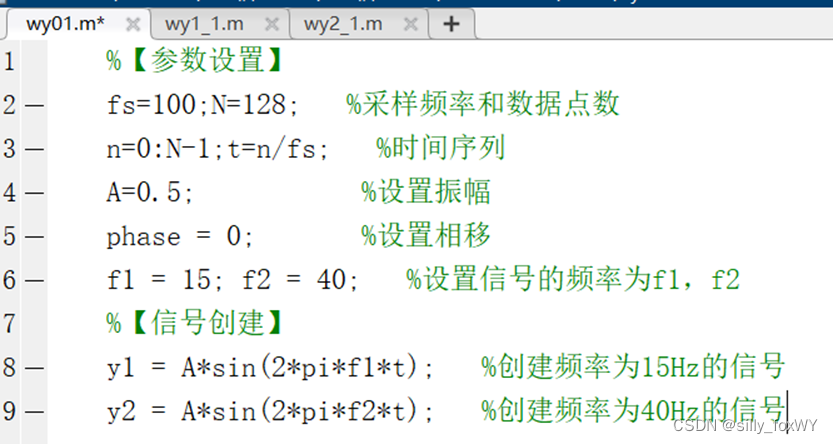
%【参数设置】
fs=100;N=128;   %采样频率和数据点数
n=0:N-1;t=n/fs;   %时间序列
A=0.5;           %设置振幅
phase = 0;       %设置相移
f1 = 15; f2 = 40;   %设置信号的频率为f1，f2
%【信号创建】
y1 = A*sin(2*pi*f1*t);   %创建频率为15Hz的信号
y2 = A*sin(2*pi*f2*t);   %创建频率为40Hz的信号
%【信号叠加】
x=y1+y2; %信号
%【fft绘制频域图】
x_fft=fft(x,N);    %对信号进行快速Fourier变换
mag=abs(x_fft);     %求得Fourier变换后的振幅
f=n*fs/N;    %频率序列
figure(1)
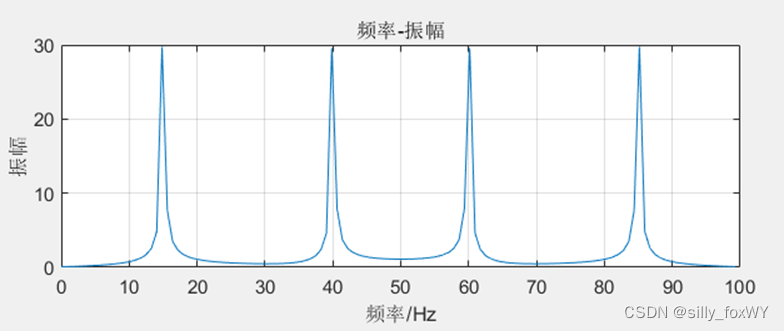
subplot(2,1,1),plot(f,mag);   %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('频率-振幅');grid on;

%【以平均能量为纵坐标】
mag2 = (abs(x_fft).^2)/N     %求平均能量
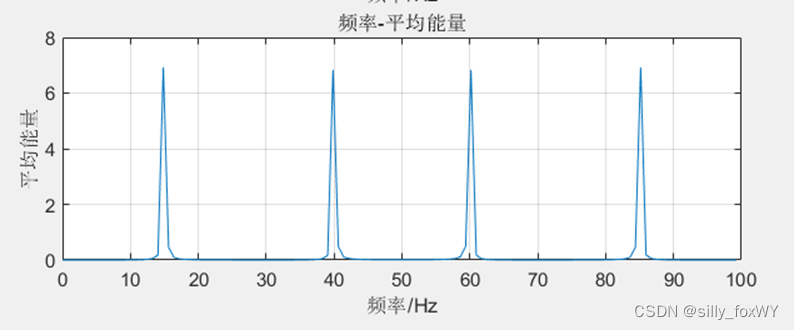
subplot(2,1,2),plot(f,mag2);   %绘出频率-平均能量图
xlabel('频率/Hz');
ylabel('平均能量');title('频率-平均能量');grid on;

%fftshift函数执行以横坐标0为中心的循环移位（以纵轴为对称轴）。
x_fft2 = fftshift(x_fft)
mag3=abs(x_fft2);     %求得Fourier变换后的振幅
mag4 = (abs(x_fft2).^2)/N     %求平均能量
figure(2)
subplot(2,1,1),plot(f,mag3);   %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('振幅');title('频率-振幅');grid on;
subplot(2,1,2),plot(f,mag4);   %绘出随频率变化的振幅
xlabel('频率/Hz');
ylabel('平均能量');title('频率-平均能量');grid on;