大家好，我是怒码少年小码。

本篇是贪心思想的跳跃问题专题，跳跃问题出现的频率很高。

跳跃游戏

LeetCode 55：给你一个非负整数数组 nums ，你最初位于数组的 第一个下标。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

• 输入：nums = [2,3,1,1,4]
• 输出：true
• 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

• 输入：nums = [3,2,1,0,4]
• 输出：false
• 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

分析：这题的关键是要搞清楚题目的意思。如果当前位置的元素是3，那么你走1/2/3步，最后如果走到的数组中的最后一个位置就算你成功！

注意： 这里很容易就陷入到底具体是跳到哪一步、走多少步的思考漩涡中。这里的关键是能否走到终点。所以我们要尽可能的跳跃到最远的位置，看当前位置最多能覆盖到哪里，如果能覆盖到终点我们就赢了！

如下图：

第一个例子中，3能覆盖{2，1，0}，2能覆盖{1，0}，1能覆盖{0}，而0不能覆盖到4，所以无法达到终点。

可见，第二个例子中有2种跳法{2，1，1，4}，{2，3，1，1，4}。

定义一个变量cover表示当前位置可以覆盖的范围，遍历指针只能在cover中的范围变化，每次i变化都要引起cover的变化（cover会得到当前位置i的元素的补充）,我们需要找到最远可以到达的位置，也就是需要在cover当前本身的值和补充之后的值之间，取一个最大值。

当cover >= nums.length - 1时，说明可以成功。

public boolean canJump(int[] nums) {
    if(nums.length == 1){
        return true;
    }
    int cover = 0 ;
    for(int i = 0 ; i<=cover;i++){
        cover = Math.max(cover , i+nums[i]);
        if(cover >= nums.length - 1){
            return true;
        }
    }
    return false;
}

最短跳跃问题

从上题可以看出一个数组有多种跳跃方式可以到达终点，那么最少需要几步能跳到终点呢？这就是LeetCode 45。

这题我们可以采用：贪心+双指针 的方法解决🤔。

• left用于遍历数组
• steps表示一共跳了多少步
• right表示当前位置能够覆盖的最大范围

maxPosition = Math.max(maxPosition,left + nums[left]);这个还是最远能跳到哪里。当left == right说明当前区间最大覆盖区间已经寻找完毕。

例如上面的第一个例子：

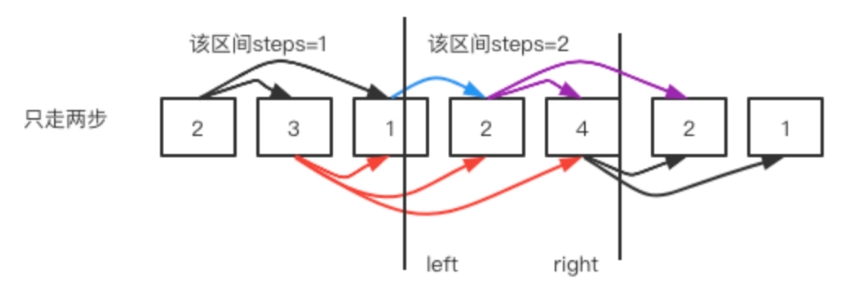
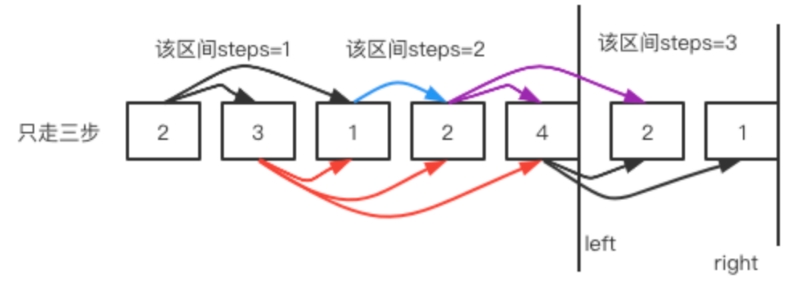
public int jump(int[] nums) {
  int right = 0 ;
  int steps = 0 ;
  int maxPosition = 0;
  for(int left = 0 ; left < nums.length - 1; left++){
      //最远能跳到哪里
      maxPosition = Math.max(maxPosition,left + nums[left]);
      if(left == right){ //left遍历到了边界，就更新边界并且步数加一
          right = maxPosition;
          steps++;
      }
      //right指针到了数组的最后
      if(right >= nums.length - 1){
          return steps;
      }
  }
  return steps;
}

END

今天这篇都是力扣上的中等难度，在面试的时候也挺常见的，多练练动手敲😎。