我们在学习编程过程中往往不仅有C语言实验报告,还有程序设计实验报告。程序设计这一科目主要是为了培养我们写代码时的计算思维,养成从问题到代码实现逐步分析,逐步深入的好习惯。前面有一篇文章介绍了部分程序设计实验报告中的编程题,今天再补充一些含新知识点的编程题,希望对大家有所帮助!
目录
1.构建一个函数int max(int xint y)求两个数的最大值,并通过该函数求任意三个整数的最大值。
2.通过函数调用,计算两个数的最小公倍数。
3.用递推法实现 cos(x)
4.用递归算法求:1+2+3+......+n。
5.用递归算法求数组元素的和。
6.用递归语句,计算x^n。其中,n是正整数。
7.用递归的方法实现十进制到八进制的转换。
8.将两个无序的一维数组排序,然后将其合并到一个一维数组中,仍保持数组有序。
9.输入一个分数,将其划为最简。例如:12/24 化简为 1/2。为了把分数约分为最简分式,首先计算分子和分母的最大公约数,然后分子和分母都除以最大公约数。求最大公约数的经典算法是Euclid算法方法如下:分别让变量m和n存储两个数的值。如果n为0,那么停止操作m中的值是最大公约数 (GCD) :否则计算m除以n的余数,把n保存到m并把余数保存到n中。然后重复上述过程,每次都先判定n是否为0。
10.有100个人围坐在一张圆桌边,座次为1~100,开始时第13座次的人先退席,以后每次数到第13个人退席,编写程序,给出退席顺序。
1.构建一个函数int max(int xint y)求两个数的最大值,并通过该函数求任意三个整数的最大值。
#include<stdio.h>
int max(int x,int y)
{
if(x>y)
return x;
else
return y;
}
int main()
{
int a,b,c,A,B,Max;
scanf("%d%d%d",&a,&b,&c);
A=max(a,b);
B=max(b,c);
Max=max(A,B);
printf("最大值为:%d",Max);
return 0;
}这题没啥讲的,不过大家在建立变量的时候可以用max1,max2,这样意思更明确。
2.通过函数调用,计算两个数的最小公倍数。
#include<stdio.h>
int Lcm(int x,int y)
{
int ret=0,i=0;
for(i=1;;i++)
{
if((x*i)%y==0)//最好还是比较大小,用大的成i,这样运算更便捷
{
ret=x*i;
break;
}
}
return ret;
}
int main()
{
int a,b;
scanf("%d%d",&a,&b);
int min=Lcm(a,b);
printf("最小公倍数是:%d",min);
return 0;
}这里唯一的知识点就是最小公倍数的求法。我这里是硬找出来,而注释中也说了可以先比较大小,用大的更快,大家可以想想为什么?(其实最小公倍数求法挺多的,大家可以多去了解几种)。
3.用递推法实现 cos(x)
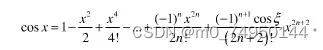
#include <stdio.h>
#include <math.h>
int main()
{
double sum=1;
double item;
int i=0;
double x=0;
printf("请输入所求x: ");
scanf("%lf",&x);
item=1;
do
{
i++;
item = -item*x*x/((2*i-1)*(2*i));
sum+=item;
}while(fabs(item)>=1e-5);
printf("自定义余弦函数cos(%lf)=%.6lf,经循环次数i=%d\n",x,sum,i);
return 0;
}其实和第8题大差不差了,主要是公式不一样,然后这边用了一个fabs函数去求绝对值。大家可以多去了解了解C语言的库函数。😀
4.用递归算法求:1+2+3+......+n。
#include<stdio.h>
int Njie(int n)
{
if(n<0)
{
printf("输入错误,无法的到正确结果\n");
return 0;
}
if(n==1)
return 1;
if(n>1)
{
return n*Njie(n-1);
}
}
int main()
{
int ret=0;
int n=0;
scanf("%d",&n);
ret=Njie(n);
printf("%d的阶乘为:%d",n,ret);
return 0;
}这题主要是多了递归算法的使用,而递归主要是要有一个结束条件,也可以叫做出口——要让程序能够从递归过程中出来,不然程序会一直运行,永远不会结束。当然,像阶乘这种一般是没有必要用递归,太占用资源,效率也不高。(具体原因和用法后面会细讲)
5.用递归算法求数组元素的和。
#include<stdio.h>
int Qiuhe(int arr[],int n)
{
if(n==0)
return arr[0];
if(n!=0)
return arr[n]+Qiuhe(arr,n-1);
}
int main()
{
int arr[100000]={0};
int n,i;
printf("请确定数组元素个数:");
scanf("%d",&n);
for(i=0;i<n;i++)
{
scanf("%d",&arr[i]);
}
int ret=Qiuhe(arr,n);
printf("%d",ret);
return 0;
}也是运用了递归思想,总之,这种只有多练才能比较敏锐发现结束条件和“套娃”模式。
6.用递归语句,计算x^n。其中,n是正整数。
#include<stdio.h>
int Pow(int x,int n)
{
if(x==0)
return 0;
else
{
int result=1;
if(n==0)
return result;
else
return result=x*Pow(x,n-1);
}
}
int main()
{
printf("这是一个计算数字n次方的程序,请输入你要计算的数字及其次方:");
int x=0;
int n=0;
scanf("%d%d",&x,&n);
int ret=Pow(x,n);
printf("ret=%d",ret);
return 0;
} 没啥可说。
7.用递归的方法实现十进制到八进制的转换。
#include<stdio.h>
int SHIBA(int x,int y)
{
int result;
if(x==0)
{
return 0;
}
else
{
return result=(x%8)*y+SHIBA(x/8,y*10);
}
}
int main()
{
int x=0;
int y=1;
printf("请输入你要转化为八进制数的十进制数:\n");
scanf("%d",&x);
int ret=SHIBA(x,y);
printf("你所输入的数字对应八进制数为:%d",ret);
return 0;
} 这个函数递归就特别了一点——它有两个参数,而且同时发生变化。这就需要先对于十进制转八进制充分了解,然后观察变化的点,这样就能更容易写出。
8.将两个无序的一维数组排序,然后将其合并到一个一维数组中,仍保持数组有序。
#include<stdio.h>
void Bubble_Sort(int*arr,int sz)
{
int i=0;
for(i=0;i<sz;i++)
{
int j=0;
for(j=0;j<sz-i;j++)
{
if(*(arr+i)>*(arr+i+j))
{
int tmp=*(arr+i);
*(arr+i)=*(arr+i+j);
*(arr+i+j)=tmp;
}
}
}
}
int main()
{
int arr1[5]={1,7,5,3,9};
int arr2[5]={2,4,8,10,6};
int arr3[10]={0};
int sz1=sizeof(arr1)/sizeof(arr1[0]);
Bubble_Sort(arr1,sz1);
int sz2=sizeof(arr2)/sizeof(arr2[0]);
Bubble_Sort(arr2,sz2);
int i=0;
for(i=0;i<sz1;i++)
{
printf("%d ",arr1[i]);
}
printf("\n");
for(i=0;i<sz2;i++)
{
printf("%d ",arr2[i]);
}
printf("\n");
int sz=sz1+sz2;
for(i=0;i<sz1;i++)
{
arr3[i]=arr1[i];
}
for(i=sz1;i<sz;i++)
{
arr3[i]=arr2[i-sz1];
}
Bubble_Sort(arr3,sz);
for(i=0;i<sz;i++)
{
printf("%d ",arr3[i]);
}
return 0;
}这题第一次提出了对于整个数组进行排序的要求,于是就引入了冒泡排序的算法,大家可以参照代码仔细品品。然后对于两个数组合为一个,我这里采用的是物理合并——建立新的数组,直接把一个个数据放进去,最后用冒泡排序再排一遍。当然大家也可以用指针再第一个数组后面续第二个数组,总之,还是那句话,多多思考,反复实验。
9.输入一个分数,将其划为最简。例如:12/24 化简为 1/2。为了把分数约分为最简分式,首先计算分子和分母的最大公约数,然后分子和分母都除以最大公约数。求最大公约数的经典算法是Euclid算法方法如下:分别让变量m和n存储两个数的值。如果n为0,那么停止操作m中的值是最大公约数 (GCD) :否则计算m除以n的余数,把n保存到m并把余数保存到n中。然后重复上述过程,每次都先判定n是否为0。
#include<stdio.h>
void FenZiMuJian(int*pa,int*pb)
{
int m=*pa;
int n=*pb;
int ret=0;
m=(m>n?m:n);
n=(m<n?m:n);
while(n!=0)
{
ret=m%n;
m=n;
n=ret;
}
*pa/=m;
*pb/=m;
}
int main()
{
int a,b;
printf("请输入分母的值a:");
scanf("%d",&a);
printf("请输入分子的值b:");
scanf("%d",&b);
FenZiMuJian(&a,&b);
printf("化简后为:%d %d",a,b);
return 0;
} 这里求最大公约数的方法其实就是辗转相除法,大家可以去了解下这个算法,理解算法的本质。然后这里也是传递地址,从而直接在函数内部完成化简,算是和函数名相吻合吧。(ps:这个函数名倒是没有水准了,各位引以为戒😅)
10.有100个人围坐在一张圆桌边,座次为1~100,开始时第13座次的人先退席,以后每次数到第13个人退席,编写程序,给出退席顺序。
#include<stdio.h>
void Exit_Sum(int sum[],int n,int num)
{
int i=0;
int count=0;
int exit=0;
for(i=0;i<num;i++)
{
sum[i]=i;
}
i=0;
do
{
if(sum[i]=i)
{
count++;
if(count==n)
{
sum[i]=-1;
exit++;
count=0;
printf("退席%3d: %0d\n",exit,i);
}
}
i=(i+1)%num;
}while(exit<num);
}
int main()
{
int sum[100]={0};
int sz=sizeof(sum)/sizeof(sum[0]);
int n=13;
Exit_Sum(sum,n,sz);
return 0;
}这个是比较有名的圆桌问题,也是比较有趣味性。这里唯一强调的是i=(i+1)%100,它是因为圆桌问题一直在转,但是i是不能超过100的。当然这里的代码还是有瑕疵的,希望大家能够认真思考,有什么想法可以发在评论区,我们可以一同探讨。(当然,关于这一题,之后会有详细介绍)