这个东西发提问没人看就发在这里了

一个球体的体积V_Sphere是容易求的：

 则我们很容易求出半径为1的圆球的体积为.

---

众所周知方程【】在三维笛卡尔坐标系中的图像为一个半径为R的圆，

则R取1时这个方程的图像就成了一个半径为1的圆。

那么我们就能推出f(x)：

但因为我们不需要z<0的那个半圆，我们就顺理成章的把这个部分去了，f(x,y)简化为了

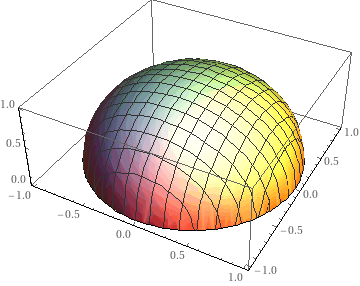
好的接下来要计算体积，则先圈定一个范围D

 然后进行二重积分

极坐标变换： 

原方程式化为： 

化简：

 

好的那么现在就非常尴尬了-_-||看看积分限上限为,下限为0，然鹅……上限不能是……

 这就麻烦了&_&事实上我们忽略\rho的部分，只看sqrt(1-rho^2)，你就发现了，这个函数的原函数是arcsin rho，而sine（正弦）函数在内是不可能出现大于1或小于-1的情况的，因此我们发现：这个积分……它不成立（至少在实数域内）

---

---

好的以上是我的问题

接下来是我的一个可能的想法

根据定积分的几何意义，为0<\rho<sqrt(2)的面积。

但是1<\rho<sqrt(2)的部分是虚数就没法解所以我们只取0<\rho<1的部分。

因此我们把方程式化为这个：

 

你看这个答案就没问题^_^求教各路大佬这个证明是否正确