---

一.利用库函数pow🍗

pow函数的原型为：

double pow(double base, double exponent);

base为底数，exponent为指数，传入两个参数，返回值是计算的结果。需要引用头文件#include<math,h>.

//方法一：利用pow函数
int main()
{
	double x, y;
	double ret = 1;
	printf("请输入两个数字 ：");
	scanf("%lf %lf", &x, &y);
	ret = pow(x, y);
	printf("%lf", ret);
	return 0;

 }

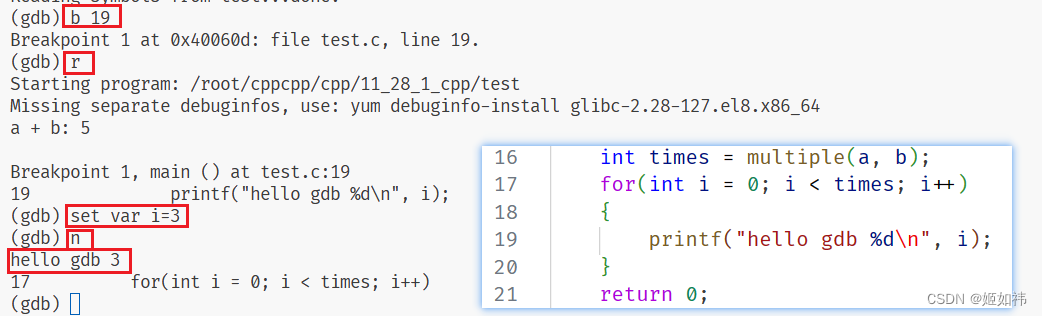
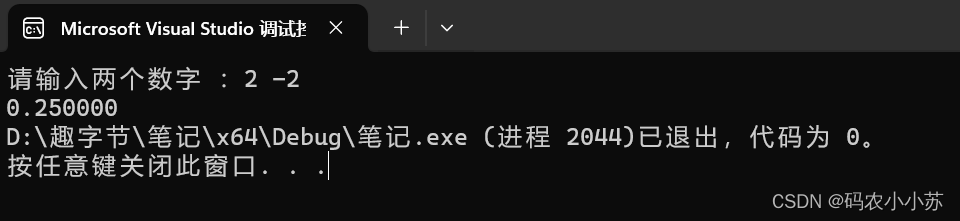
运行结果

---

二.自己实现mypow函数🍗

利用一个for循环，一直乘n次即可，值得注意的是负号问题，如果指数是符号，我们需要先把它转为正号，然后再写。还有注意指数和底如果为0的话需要单独拿出来讨论。

#define _CRT_SECURE_NO_WARNINGS//这一句必须放在第一行
#include <stdio.h>
#include <math.h>
//方法二：自己实现（未优化）
double Mypow(double x, double n)
{
	if (x == 0)
		return 0;
	if (n == 0)
		return 1;
	int flg = 1;
	double tmp=1;
	if (n < 0)
	{
		flg = -1;//作为标记
		n = -n;
	}
	for (int i = 1;i <= n;i++)
	{
		tmp *= x;
	}
	return (flg == 1) ? tmp : 1 / tmp;//标记为1表示指数为正，为-1则表示指数为负
}
int main()
{
	double x, n;
	printf("请输入两个数字 :");
	scanf("%lf %lf", &x, &n);
	double ret = Mypow(x, n);
	printf("%lf", ret);
}

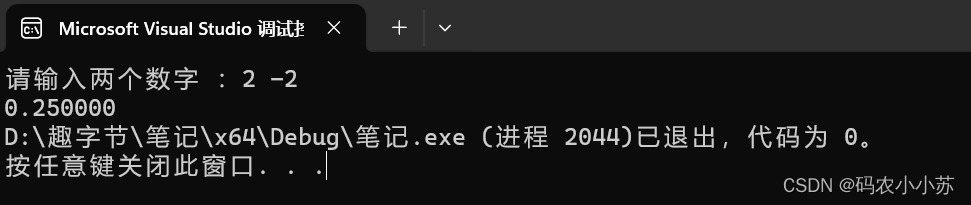
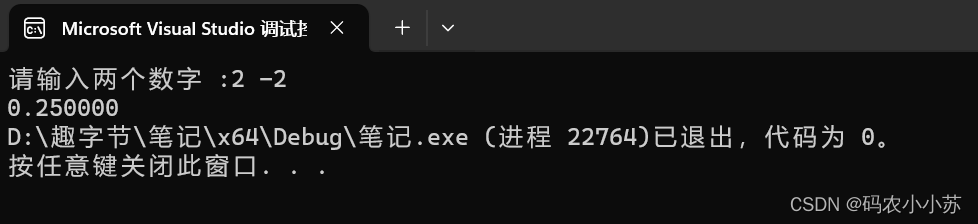
运行结果

---

 三.自己实现mypow函数(代码优化)🍗

力扣中有一个题目就是让我们自己实现mypow函数，我们先把上面的代码放到力扣中看看是什么样子。

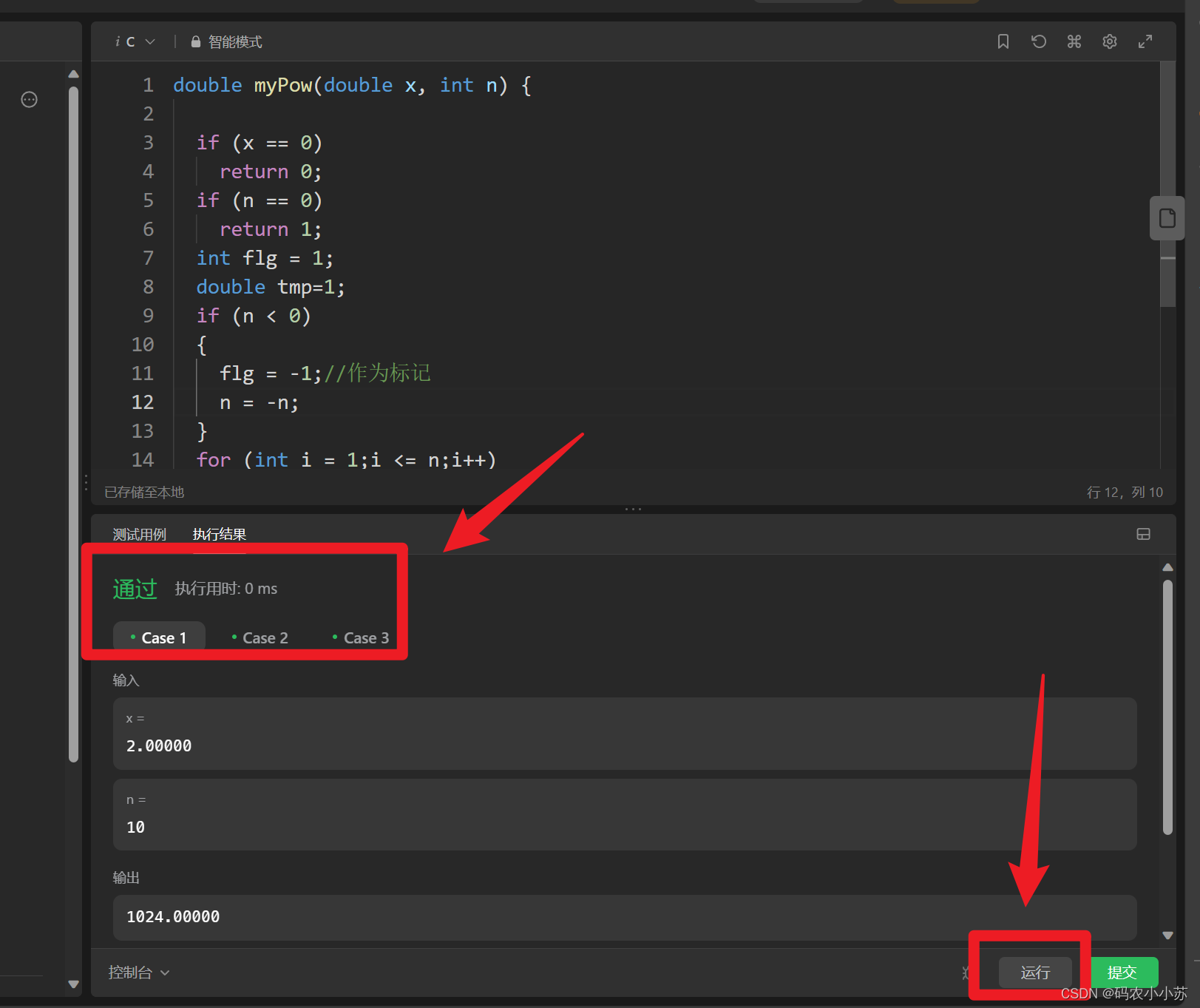
 点击运行之后，测试用例都通过了，但是点击提交后...

 显示超出时间限制，说当x=0.00001，n=2147483647时，测试通不过。

接下来我们来看一下代码是如何进行优化的

 这样就不需要乘以n次，而只需要乘logn，时间复杂度变为logn。

#define _CRT_SECURE_NO_WARNINGS//这一句必须放在第一行
#include <stdio.h>
#include <math.h>
//优化后的代码
double Pow(double x, long long y)//x!=0,y>=0
{
	if (y == 0)
		return 1;
	double tmp = Pow(x, y / 2);
	if (y % 2 != 0)//奇数
		return tmp * tmp * x;
	else//偶数
		return tmp * tmp;
}

double Mypow(double x, long long n) 
{
	long long y = n;
	if (x == 0)
		return 0;
	if (n == 0)
		return 1;
	int flg = 1;
	if (n < 0)
	{
		flg = -1;
		y = -(long long)n;
	}
	double tmp = Pow(x, y);
	return (flg == 1) ? tmp : 1 / tmp;
}
int main()
{
	double x;
	long long n;
	printf("请输入两个数字 :");
	scanf("%lf %lld", &x, &n);
	double ret = Mypow(x, n);
	printf("%lf", ret);
}

运行结果

 放在力扣中

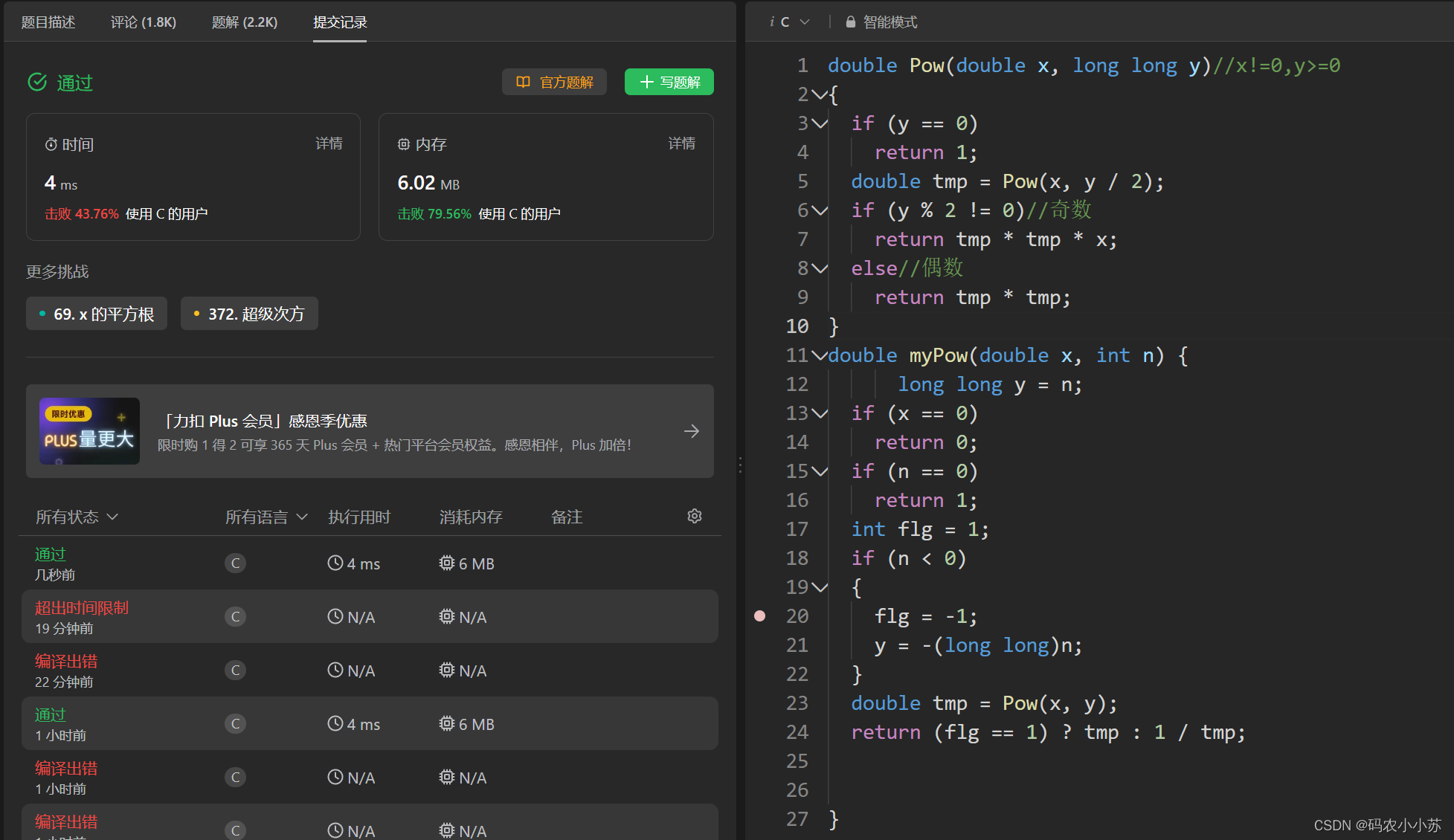
 现在的代码就编译通过了。

---

今天的分享就到这里啦！🍗喜欢的小伙伴们可以给一个免费的赞表示对博主的支持🍗，你们的支持就是我创作的最大动力。