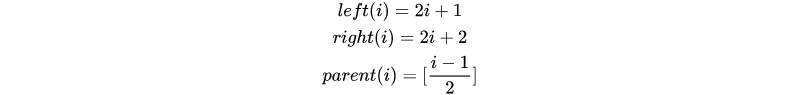题目
迷宫与陷阱 - 蓝桥云课 (lanqiao.cn)
https://www.lanqiao.cn/problems/229/learning/?page=1&first_category_id=1&name=%E8%BF%B7%E5%AE%AB%E4%B8%8E%E9%99%B7%E9%98%B1
思路和解题方法
- 首先，定义了一个结构体
node来表示迷宫中的每个节点，包括节点的坐标(x, y)、已经走过的步数cnt和当前状态status（即无敌时间还剩余多少步）。同时，定义了一个二维数组a来表示迷宫的地图，一个二维数组vis来标记节点是否被走过，一个二维数组s来保存节点的状态。- 接下来，通过输入获取迷宫的大小
n和能力值k。然后，使用嵌套循环读取每个节点的状态，并将其保存在地图数组a中。- 之后，定义了方向数组
nex和ney，分别表示在x方向和y方向上的移动。然后，创建一个队列que，用于存储待遍历的节点。- 接下来，将起点
(1, 1)添加到队列中，并标记起点已经走过。然后开始一个循环，直到队列为空为止。在每次循环中，取出队列的第一个节点temp，并将其弹出队列。- 然后，对四个方向进行遍历，计算下一个节点的坐标
(x, y)。通过调用check()函数来检查下一个节点是否能够到达。如果可以到达，则更新状态，并将下一个节点加入队列。- 如果下一个节点是道具格（用
%表示），则更新状态为无敌状态，并将状态保存到状态数组s中。然后标记该节点已经走过，并将其加入队列。- 如果下一个节点之前已经走过，并且当时的无敌状态比现在的状态更好，则不需要再走一次。否则，将下一个节点加入队列。
- 最后，当到达终点时，返回最短路径的步数。
- 整个算法的思路是通过广度优先搜索遍历迷宫中的所有可达节点，并记录到达每个节点时的步数和状态。通过不断更新状态和比较最优状态，找到从起点到终点的最短路径。
复杂度
时间复杂度:
O(n^2*k)
时间复杂度为O(n^2*k)，其中n为迷宫大小，k为能力值。原因是最坏情况下需要遍历所有的节点，并且每个节点可能对应k种不同的状态。
空间复杂度
O(n^2*k)
空间复杂度也为O(n^2*k)，原因是需要存储地图数组a、标记数组vis和状态数组s，以及队列que中的节点信息。需要注意的是，这里的空间复杂度是个常数倍，具体大小取决于迷宫的大小和能力值的范围。
c++ 代码
#include<iostream>
#include<queue>
using namespace std;
const int N = 1010;
struct node
{
int x, y; // 节点的坐标
int cnt; // 节点已经走过的步数
int status; // 当前的状态，即无敌时间还剩余多少步
};
int a[N][N] = { 0 }, vis[N][N] = { 0 }, s[N][N] = { 0 }; // 地图a、标记数组vis、状态数组s
int n, k; // 地图大小n和能力值k
int nex[4] = { 1,0,-1,0 }; // 方向数组，表示x方向的移动
int ney[4] = { 0,1,0,-1 }; // 方向数组，表示y方向的移动
// 检查下一个节点是否能够到达
bool check(int x, int y, int st)
{
if (x > n || y > n || x < 1 || y < 1 || a[x][y] == '#') return false; // 出界或者撞墙
if (st == 0 && a[x][y] == 'X') return false; // 非无敌撞陷阱
return true;
}
int bfs()
{
queue<node> que; // 存储待遍历的节点
que.push(node{ 1,1,0,0 }); // 起点
vis[1][1] = 1; // 标记起点被走过
while (!que.empty()) // 当队列不为空时进行循环
{
node temp = que.front(); // 取出队列的第一个节点
que.pop(); // 将队列的第一个节点弹出
if (temp.x == n && temp.y == n) return temp.cnt; // 如果到达终点，返回最短路径的步数
for (int i = 0; i < 4; i++) // 在四个方向上进行遍历
{
int x = temp.x + nex[i], y = temp.y + ney[i]; // 计算下一个节点的坐标
if (check(x, y, temp.status)) // 如果可以走
{
int status1 = 0 > temp.status - 1 ? 0 : temp.status - 1; // 更新状态，此时的状态是x,y时的
int status2 = max(temp.status - 1, 0);
int status = status1;
if (a[x][y] == '%') // 如果是道具格
{
status = k; // 更新状态为无敌状态
s[x][y] = status; // 将状态保存到状态数组中
a[x][y] = 0; // 走过道具格之后就变成普通格子
vis[x][y] = 1; // 标记走过
que.push(node{ x,y,temp.cnt + 1,status }); // 将下一个节点加入队列
}
else {
if (!vis[x][y]) // 如果没有走过，有必要走一次
{
vis[x][y] = 1; // 标记走过
s[x][y] = status;
que.push(node{ x,y,temp.cnt + 1,status }); // 将下一个节点加入队列
}
if (status <= s[x][y]) // 之前走过，并且当时的无敌状态更好
continue;
else {
que.push(node{ x,y,temp.cnt + 1,status }); // 否则，如果之前走过但是无敌状态没有再一次走的时候好，有必要再走一次
}
}
}
}
}
}
int main()
{
cin >> n >> k; // 输入迷宫地图大小和能力值k
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
char c;
cin >> c;
a[i][j] = c; // 输入每个节点的状态
}
cout << bfs() << endl; // 输出最短路径的步数
return 0;
}
觉得有用的话可以点点赞，支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
