奇异值分解

SVD是一个很有用的矩阵因子化方法。
SVD提出的目的：任何一个$m\times n$的矩阵都可以当作一个超椭圆（高维空间的椭圆），可以把它们当作单位球体S的像。
一个超椭圆可以通过将单位球型在正交方向${\mathbf{u}}_1,{\mathbf{u}}_2,...,{\mathbf{u}}_{\mathbf{m}}$通过缩放因子${\sigma }_1,...,{\sigma }_m$，其中m是维度，如果在平面上m=2

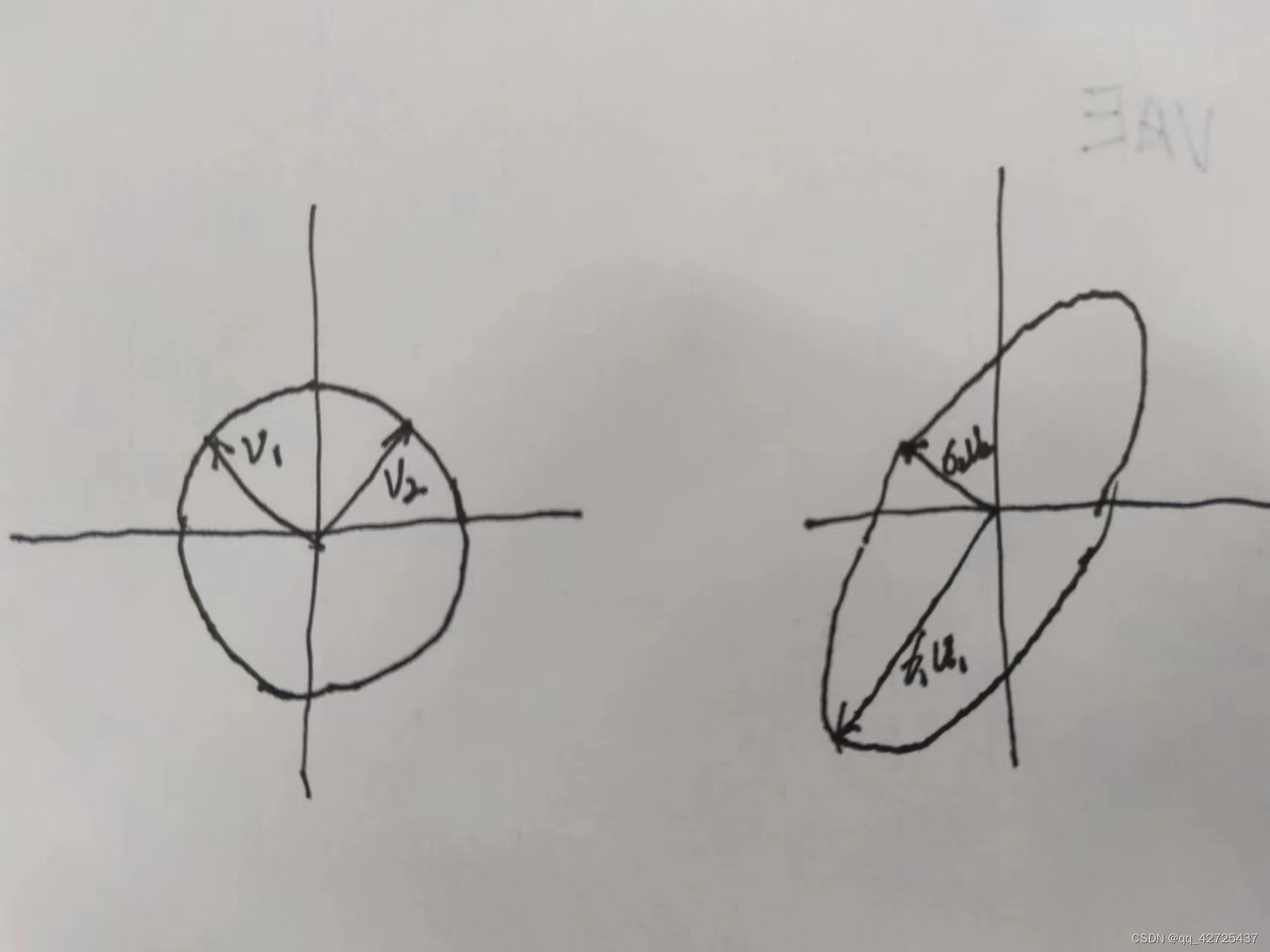
通过上面这张图，可以做出下面的定义：

1. singular value:${\sigma }_1,...,{\sigma }_n\ge 0$一般假设${\sigma }_1\ge {\sigma }_2\ge ...$
2. Light singular vectors:${\mathbf{u}}_1,{\mathbf{u}}_2,...,{\mathbf{u}}_{\mathbf{n}}$,单位向量
3. right singular vectors:${\mathbf{v}}_1,{\mathbf{v}}_2,...,{\mathbf{v}}_{\mathbf{n}}$是ui的逆向满足$A{v}_i={\sigma }_i{u}_i$
   这个名字中左和右来自svd的公式。
   把上面的公式矩阵化，可以得到：
   $$AV=\hat{U}\hat{\Sigma }$$
   在这里面
4. $\hat{\Sigma }\in {\mathbb{R}}^{n\times n}$是一个非负数对角矩阵
5. $\hat{U}\in {\mathbb{R}}^{m\times n}$是一个列正交矩阵
6. $V\in {\mathbb{R}}^{n\times n}$是一个列正交矩阵
   因此V是个正交矩阵，因为它是基向量，因此我们就可以得到reduced SVD：
   $$A=\hat{U}\hat{\Sigma }{V}^T$$
   正如QR分解一样，可以把扩充$\hat{U}$的列使得$U\in {\mathbb{R}}^{m\times m}$
   然后需要给$\hat{\Sigma }$添加一些为为0的行，使得可以沉默掉新添加到U中的随机列，这样就得到了完全SVD
   $$A=U\Sigma V^T$$
   对比reduced和full
   
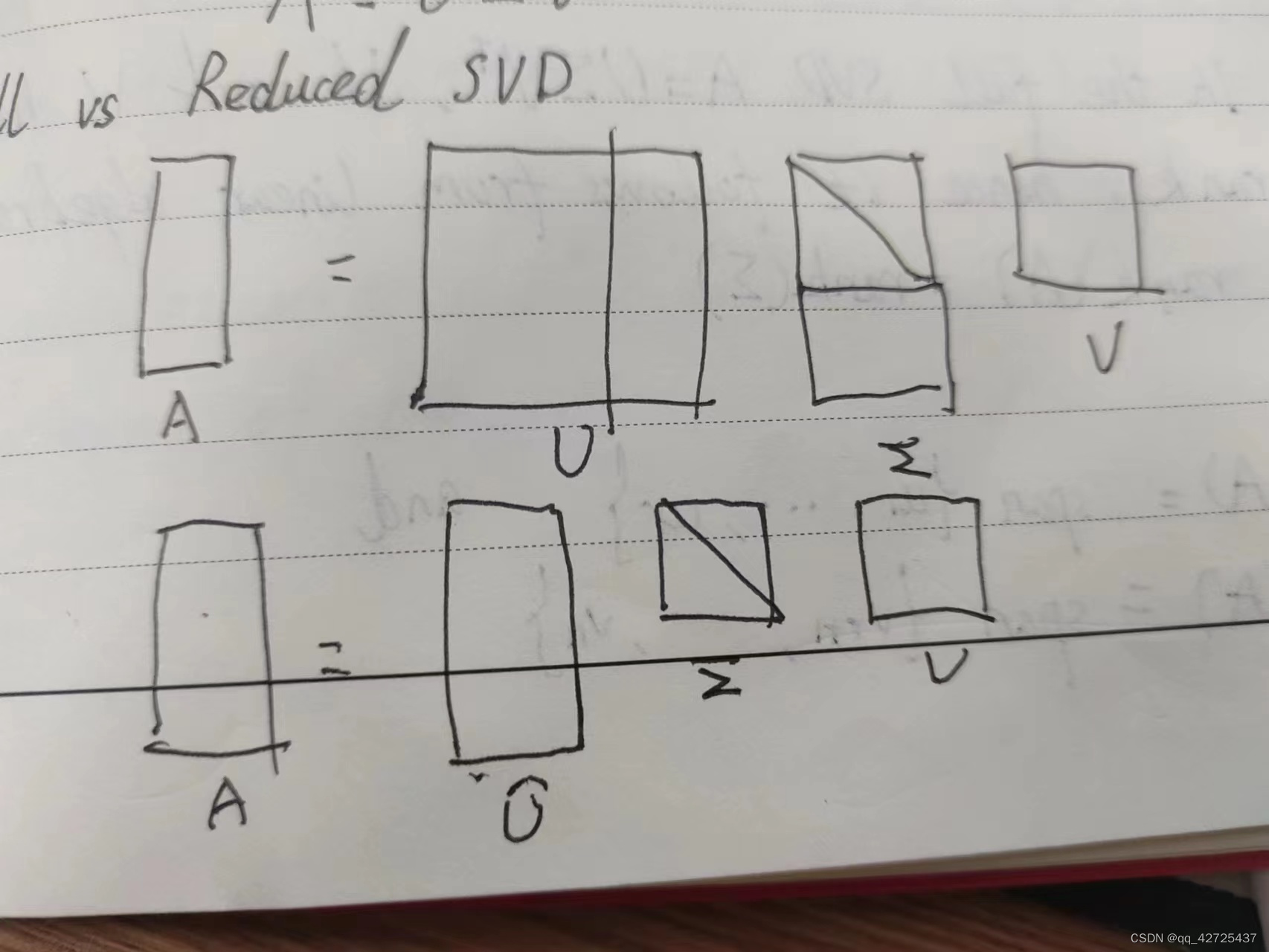
   现在重新考虑当时把球型变为超椭圆型的目的。
   1 $V^T$是球型S
   2 $\Sigma$拉伸球型得到椭球形
   3 $U$旋转投射而不改变形状

通过SVD可以知道一些矩阵性质

1. A的秩为r，也就是非零奇异值的个数
   proof:U和V是满秩的，所以rank（A） = rank($\Sigma$)
2. image(A) = span{${\mathbf{u}}_1,{\mathbf{u}}_2,...,{\mathbf{u}}_{\mathbf{r}}$}
   null(A) = span{${\mathbf{v}}_{\mathbf{r}+1},...,{\mathbf{v}}_{\mathbf{n}}$}
3. $||A|{|}_2={\sigma }_1$
   proof:$||A|{|}_2\equiv ma{x}_{||V|{|}_2=1}$||Av||_2
4. A的奇异值是AAT的特征值的平方根。
   根据上面的性质：可以知道SVD的两种应用

长方形矩阵的条件数

$K(A)=||A||||A^{+}||$
其中$A^{+}$是伪逆

• $||A|{|}_2={\sigma }_{max}$
• $||A^{+}|{|}_2=\frac{1}{{\sigma }_{min}}$
  所以$K(A)=\frac{{\sigma }_{max}}{{\sigma }_{min}}$

低秩近似

把SVD变为
$$A=\sum _{j=1}^r{\sigma }_j{u}_j{v}_j^T$$
每个$u_j{v}_j^T$都是一个秩为1的矩阵
Theorem:
对于$0\le v\le r$,让$Av={\sum }_{j=1}^v{\sigma }_j{u}_j{v}_j^T$
所以
$$||A-Av|{|}_2=\underset{B\in {\mathbb{R}}^{m\times n},rank(B)\le v}{\inf }||A-B|{|}_2$$
同样的也可以在Frobenius norm中证明，这个理论说明SVD是压缩矩阵的一个好的方法。