题目

---

二叉树的最近公共祖先

---

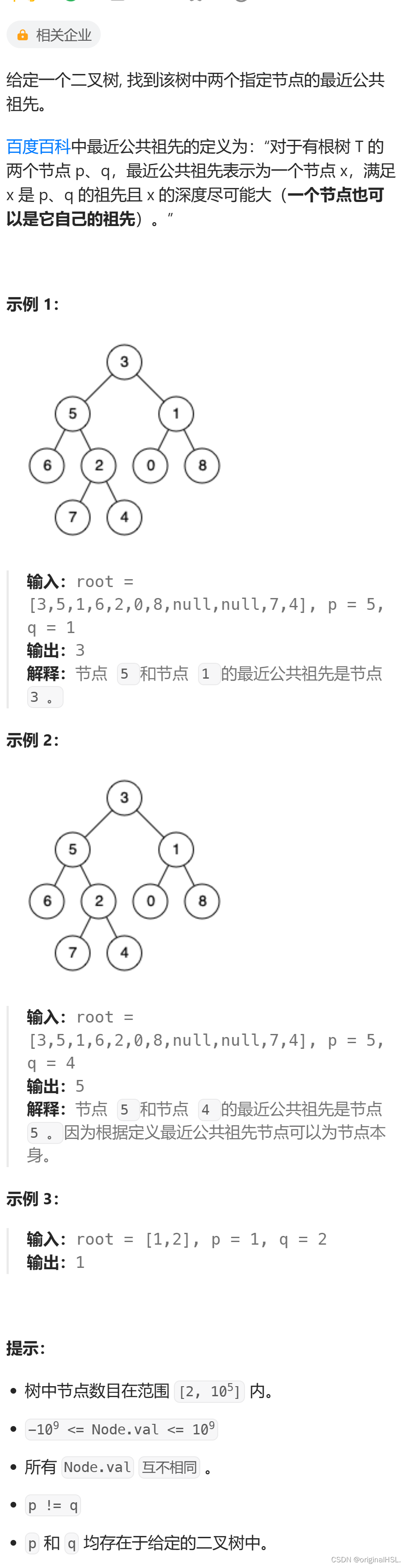
思路

我们可以通过两个栈来实现

实现一个FindPath函数，用来查找从根节点到目标节点的路径（路径可以用栈来保存）

路径保存好后，
再使用两个循环来比较栈Ppath和Qpath的大小，使得两个栈的大小相等。
然后，再使用一个循环来比较栈顶元素，直到找到最低公共祖先。在每一次比较过程中，如果栈顶元素不相等，就分别从两个栈中弹出栈顶元素，直到找到最低公共祖先。

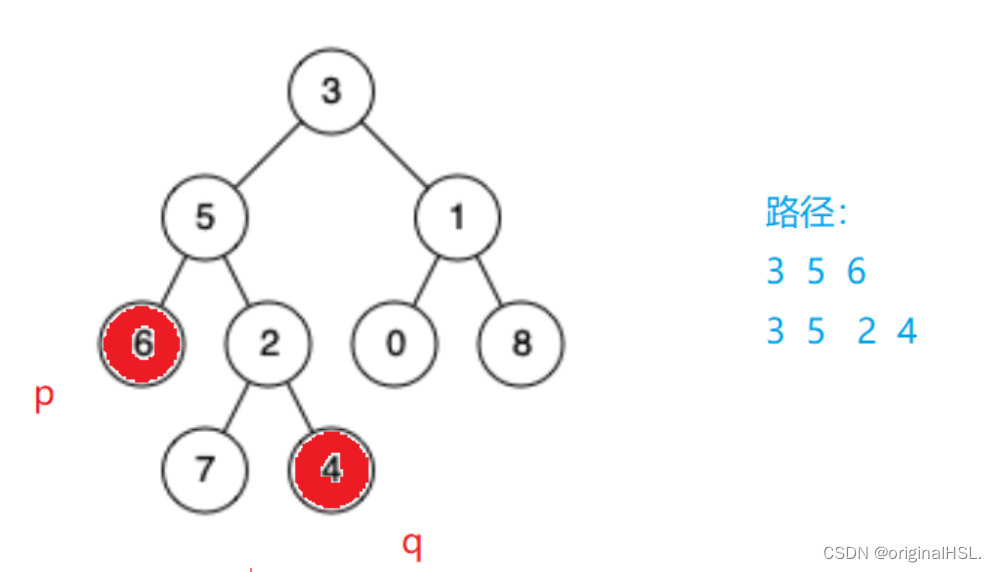
操作如下：

1. 在lowestCommonAncestor函数中，声明两个栈Ppath和Qpath，用于保存从根节点到节点p和q的路径。

2. 调用FindPath函数两次，分别查找节点p和q的路径。FindPath函数是一个递归函数，用于在二叉树中查找节点x的路径，并将路径保存在给定的栈path中。

3. 在FindPath函数中，首先判断当前节点root是否为空，如果为空，则返回false。然后，将当前节点root压入栈path中。

4. 接着，判断当前节点root是否等于目标节点x，如果是，则返回true，表示已经找到目标节点。

5. 如果目标节点不在当前节点root上，那么就递归地在左子树和右子树中查找目标节点。如果在左子树中找到目标节点，则返回true，表示已经找到目标节点。如果在右子树中找到目标节点，则同样返回true。

6. 如果左子树和右子树都没有找到目标节点，则说明当前节点不在最终路径上，需要将其从栈path中弹出，并返回false。

7. 回到lowestCommonAncestor函数，使用两个循环来比较栈Ppath和Qpath的大小，使得两个栈的大小相等。

8. 然后，再使用一个循环来比较栈顶元素，直到找到最低公共祖先。在每一次比较过程中，如果栈顶元素不相等，就分别从两个栈中弹出栈顶元素，直到找到最低公共祖先。

9. 最后，返回栈Qpath的栈顶元素，即为最低公共祖先节点。

代码（详细注释）

class Solution {
public:
    // 查找从根节点到目标节点的路径
    bool FindPath(TreeNode *root, TreeNode *x, stack<TreeNode*>& path) {
        if (root == nullptr) {
            return false; // 当前节点为空，返回false
        }
        path.push(root); // 将当前节点加入路径
        if (x == root) {
            return true; // 找到目标节点，返回true
        }
        if (FindPath(root->left, x, path)) {
            return true; // 在左子树中找到目标节点，返回true
        }
        if (FindPath(root->right, x, path)) {
            return true; // 在右子树中找到目标节点，返回true
        }
        path.pop(); // 当前节点不在路径上，弹出当前节点
        return false; // 返回false
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> Ppath; // 保存节点p的路径
        stack<TreeNode*> Qpath; // 保存节点q的路径
        
        FindPath(root, p, Ppath); // 查找节点p的路径
        FindPath(root, q, Qpath); // 查找节点q的路径

        // 使得两个路径的长度相等
        while (Ppath.size() != Qpath.size()) {
            if (Ppath.size() > Qpath.size()) {
                Ppath.pop(); // 如果Ppath路径长，弹出Ppath的栈顶元素
            } else {
                Qpath.pop(); // 如果Qpath路径长，弹出Qpath的栈顶元素
            }
        }

        // 逐个比较两个路径上的节点，找到最低公共祖先
        while (Ppath.top() != Qpath.top()) {
            Qpath.pop(); // 弹出Qpath栈顶元素
            Ppath.pop(); // 弹出Ppath栈顶元素
        }

        return Qpath.top(); // 返回最低公共祖先节点
    }
};

（本题完）