一、前言:
这是怀化学院的:Java数据结构中的一道中等编程题(此方法为博主自己研究,问题基本解决,若有bug欢迎下方评论,我会第一时间改进代码,谢谢!) 后面其他编程题只要我写完成功,会陆续更新,记得三连哈哈!
二、题目要求如下:
(第 11 题) 数制转换(难度系数75)
数制转换
标准输入输出
题目描述:
数制转换。(要求采用栈实现,练习进栈入栈函数的编写)
输入:
输入的第一行包含两个数,n,d
n表示要转换的数的个数
d表示要转换成的进制数
接下来是n个十进制数输出:
对每一测试用例,用一行输出数制转换后的结果
输入样例:
2 8
123
213
输出样例:
173
325
三、代码实现(这里我是用顺序栈去实现数制转换,基本原理代码解释在注释中)
(1)自定义基础栈接口:
package com.feisi.convert;
//自定义一个栈接口,对栈的所有操作都在其中
public interface Stack {
//都是抽象方法
public abstract int push(int item); //入栈
public abstract int pop(); //出栈
public abstract int peek(); //取出栈顶元素
public abstract int size(); //返回栈中的元素个数
public abstract boolean isEmpty(); //判断栈是否为空
}(2) 自定义顺序栈类,并让它去实现自定义基础栈接口:(里面包含了顺序栈的基本操作方法)
package com.feisi.convert;
import java.util.Arrays; //用里面的扩容数组的方法,所以要导入这个包
public class MyStack implements Stack {
//用private封装,安全
private int maxSize; //顺序栈的容量
private int[] data; //自己创建一个数组,用来存储顺序栈中的数据元素
private int top; //用来指向顺序栈的栈顶
//用构造方法来初始化栈
public MyStack(){
data=new int[100];//实现顺序栈的数组初始容量100
top=-1; //栈空的时候指向-1下标
}
//防止初始化时,原来的数组长度不满足题目要求
public void expand(int []data) {
//导入了包直接类调用
//将原来数组长度扩容原来长度的2倍
if (maxSize == data.length) {
Arrays.copyOf(data, data.length * 2);
}
}
//实现接口中的所有抽象方法
//压栈
@Override
public int push(int item) {
if(top!=(data.length-1)){
data[++top]=item; //要先让top++自增,也就是给数组第一个元素赋值
return item;
}else{
System.out.println("栈已满");
return 0;
}
}
//出栈
@Override
public int pop() {
int item=0;
if(!isEmpty()){
item=data[top--];
}
return item; //返回出栈的值,因为top已经减1了这时
}
//取出栈顶元素
@Override
public int peek() {
int item =0;
if(!isEmpty()){
item=data[top]; //top指向的元素永远是栈顶的那个
}
return item;
}
//求栈的长度
@Override
public int size() {
return (this.top+1); //自己想一下逻辑就知道了
}
//判断栈是否为空
@Override
public boolean isEmpty() {
if(top==-1){
return true;
}
else{
return false;
}
}
}
(3) 自定义实现栈类:里面有数制转化的方法,在测试类去创建实例,调用它里方法并完成数制的转换。
package com.feisi.convert;
public class ImplementStack {
MyStack myStack = new MyStack();
public void convert(int num,int d){
//记录余数
int remainder=0; //注意不能写访问修饰符public等等,因为局部变量
//记录商(取整后的)
int sum=num;
while(sum>=d){ //因为只要商不小于对应的进制数,就要继续对进制数取余
remainder = sum % d; //传进的十进制数对进制数取余(为啥这样可以自己了解进制转换原理)
myStack.push(remainder); //将第一个余数压入栈中,因为取余后逆置输出,刚好最后入栈的余数第一个先出栈(栈的原理)
sum=sum/d; //更新商,进行下一次取余
}
myStack.push(sum); //这一步其实就是把最后小于进制数的商压栈,因为最后的余数就是商的本身(自己理解理解)
}
//此方法最大作用就是依次把余数弹栈
public void printf(int d){
while(!myStack.isEmpty()){
int x=myStack.peek();
if((d==16)&&x==10||x==11||x==12||x==13||x==14||x==15) { //该地方用来输出当转化成16进制的格式代码
if(x==10){
System.out.print('A');
}else if(x==11){
System.out.print('B');
}else if(x==12){
System.out.print('C');
}else if(x==13){
System.out.print('D');
}else if(x==14){
System.out.print('E');
}else if(x==15){
System.out.print('F');
}
}else{
System.out.print(x); //先输出栈顶元素再出栈,也就是top--
}
myStack.pop(); //每次输出栈顶元素后记得出栈噢
}
System.out.println();
}
}
(4)自定义测试类,用来完成各数制转换的测试:
package com.feisi.test;
import com.feisi.convert.ImplementStack;
import com.feisi.convert.MyStack;//因为测试类与自己创建的栈类不在同一个包里,所以我才导包
import java.util.Scanner;
public class Test_Stack {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); //代表要转换的十进制数的个数
int d = sc.nextInt(); //代表所要转的某种进制
int num[] = new int[n]; //存储n个十进制数
for (int i = 0; i < n; i++) {
num[i] = sc.nextInt();
}
for(int j=0;j<num.length;j++){
ImplementStack i = new ImplementStack();
i.convert(num[j],d);
i.printf(d);
}
}
}四、所有情况的代码运行情况:
<1>当需要转换的进制是二进制时:

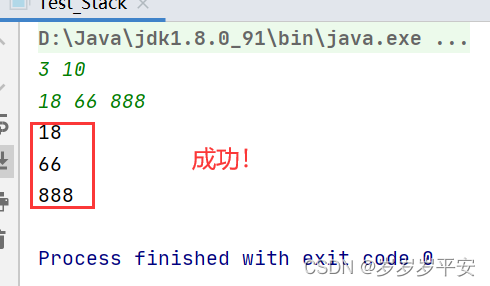
<2> 当需要转换的进制是八进制时:
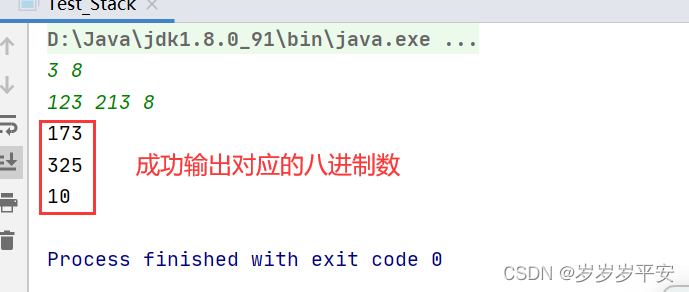
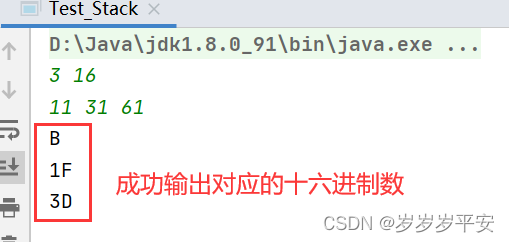
<3> 当需要转换的进制是十六进制时:
<4>当需要转换的进制是十进制时:(这个当然不用说肯定可以)