TDL：(Tapped Delay Line，抽头延迟线)
CDL：(Clustered Delay Line，集群延迟线)

一 TDL

1. 定义：由一组不同衰落系数和不同时延的抽头组成。全频率范围为：0.5GHz~100GHz，最大带宽2GHz ,TDL是简化模型，本身为SISO设计，但可通过重复多次加引入空间相关性对MIMO信道建模
   

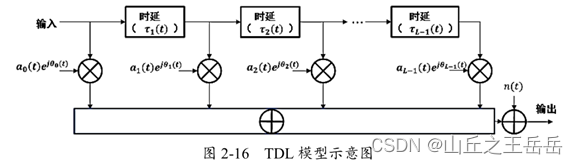
2. 分类:

   • NLos信道场景：TDL-A、TDL-B、TDL-C，TDL-A和TDL-B有23个抽头，TDL-C有24个抽头
   • Los信道场景：TDL-D、TDL-E，TDL-D有 13 个抽头，TDL-E有14 个抽头，每个抽头延迟和相对功率不同

3. 抽头特性

   • 每个抽头的多普勒频移有典型的Jakes频谱形状（常用瑞利衰落模型，频谱形状为U型谱）和最大多普勒频移f_D（$f_D=\frac{|v|}{{\lambda }_0}$）
   • TDL-D TDL-E是LOS路径。所以其第一个抽头服从Ricean fading分布
   • 这些抽头，多普勒频普在多普勒频移$f_s=0.7f_D$处还包含一个峰值，幅度为生成衰落分布时指定K因子。‘

4. 每个TDL模型都能在延迟上进行缩放，以使模型达到期望的RMS（Root Mean Square）延迟扩展

5. TDL模型适用于窄带信道建模，其多径的分辨率较低，在一个可分辨率的附加时延内，可能有两个或多个多径信号到达，但这些多径信号不可分辨，其适量组合成单一多径信号的瞬时幅度和相位。

6. TDL信道模型的信道系数
   $$h(t;\tau )=\sum _{N=1}^N{a}_n(t){\mu }_n(t)\delta (t-{\tau }_n)$$
   $a_n(t)$是n个抽头的增益
   ${\mu }_n(t)$是由多条不可分辨路径组合得到的瑞利衰落信号
   ${\tau }_n$是n个抽头的时延

二 CDL

1. 定义：频率范围：0.5GHz~100GHz，最大带宽为2GHz
   
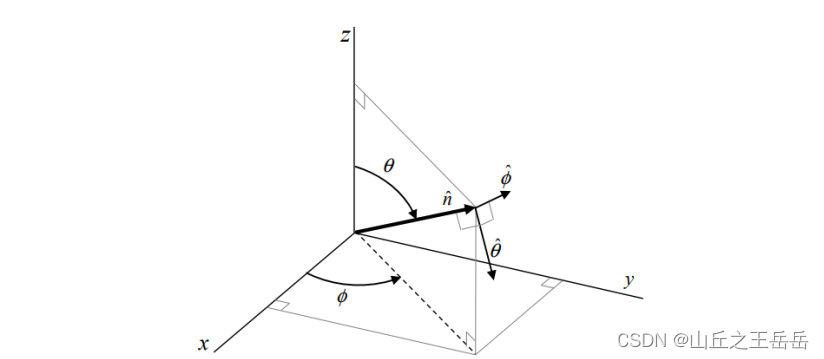
2. 分类
   • NLos信道场景：CDL-A、CDL-B、CDL-C
   • Los信道场景：CDL-D、CDL-E
3. CDL簇数量最多有24个，可以表征更多波束
4. 信道脉冲响应为：
   $$h(\tau ;t)=\sum _{l=0}^{\infty }\sum _{k=0}^{\infty }{a}_{k,l}(t)e^{j{\phi }_{k,l}(t)}\delta (\tau -T_l-{\tau }_k)$$
   $a_{k,l}、{\phi }_{k,l}$是第$l$簇中第$k$径的增益和相位
   $T_l$为第l簇的延时
   ${\tau }_{k,l}$为第$l$簇中第$k$径的延迟

三 CDL TDL区别

1. CDL引入簇，簇是具有相似到达角、离开角、和时延的多径集合
2. 除了时延和功率两个参数外，CDL模型增加了离开方位角（AoD）、到达方位角(AoA)、离开天顶角(ZoD)、到达天顶角(ZoA)，用来表征信道模型的空间特性，为3D信道设计，更好表征空间相关性。
3. TDL和CDL可以根据实际仿真需要调整均方根时延扩展
   $${\tau }_{n,scaled}={\tau }_{n,model}\ast D{S}_{desired}$$
4. CDL/TDL-D和CDL/TDL-E的LOS信道模型，可以调整K因子，设期望调整的K因子为K_desired,CDL/TDL功率为：
   $$K_{model}=P_{l,model}^{LOS}-10lo{g}_{10}(\sum _{n=1}^{N}10^{P_{n,model}/10})$$
   功率调整完成后，需要对时延扩展重新进行计算。
   调整K因子的本质：调整各个簇、抽头之间的功率。K因子越大，第一个簇、抽头中视距径功率越大，在通信中视距径分量占比重越大
5. 角度调整
   CDL预定义的角度值可以通过引入角度平移和缩放来推广，平移改变平均角度，缩放改变角度扩展
   $${\varphi }_{n,scaled}=\frac{A{S}_{desired}}{A{S}_{model}}({\varphi }_{n,model}-{\mu }_{\varphi ,model})+{\mu }_{\varphi ,desired}$$

参考
5G通信中的TDL模型
移动通信基础（13）TDL、CDL、信道相关性
TDL、CDL信道模型简述