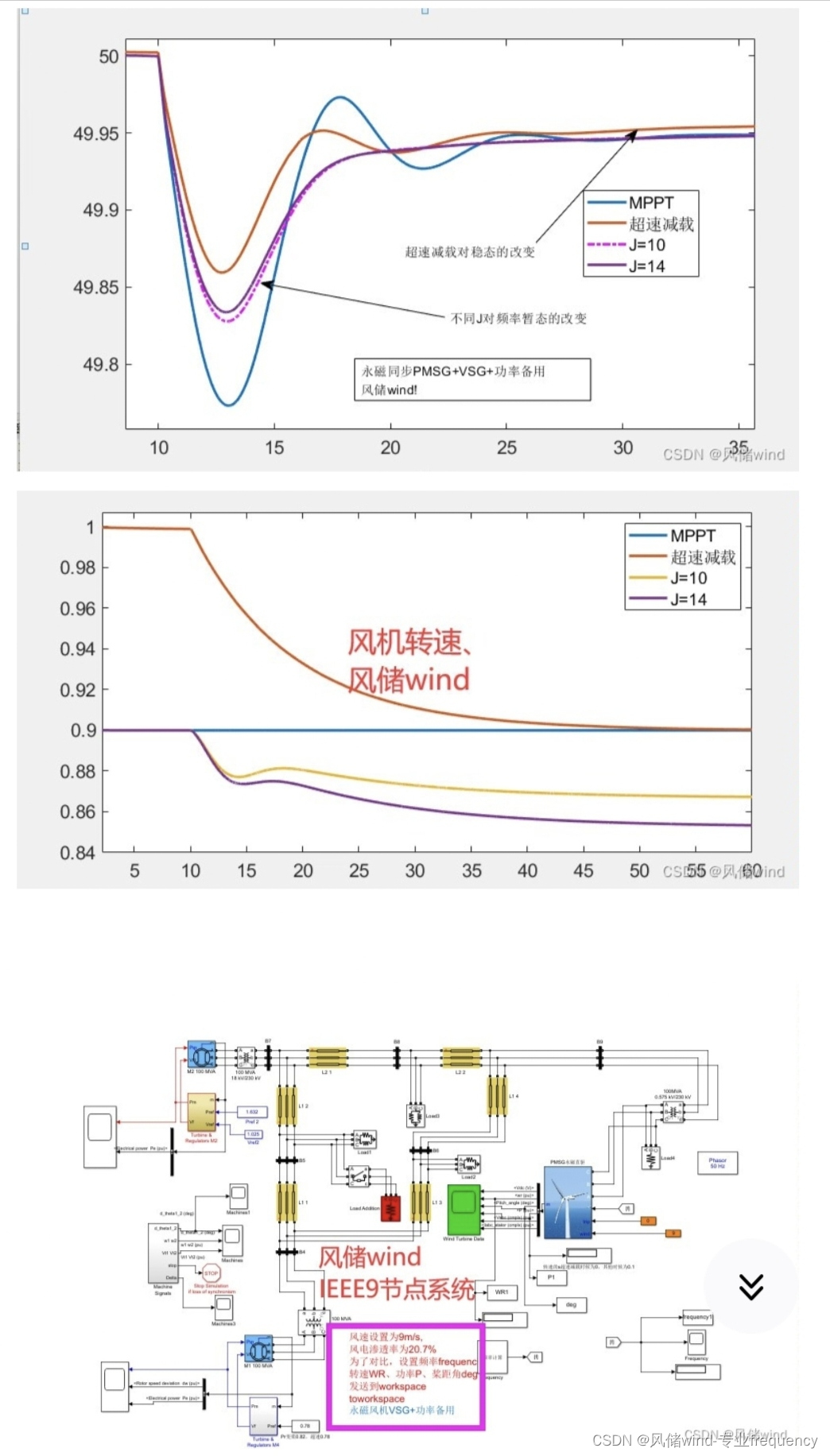
KMP算法

KMP算法是一种改进的字符串匹配算法

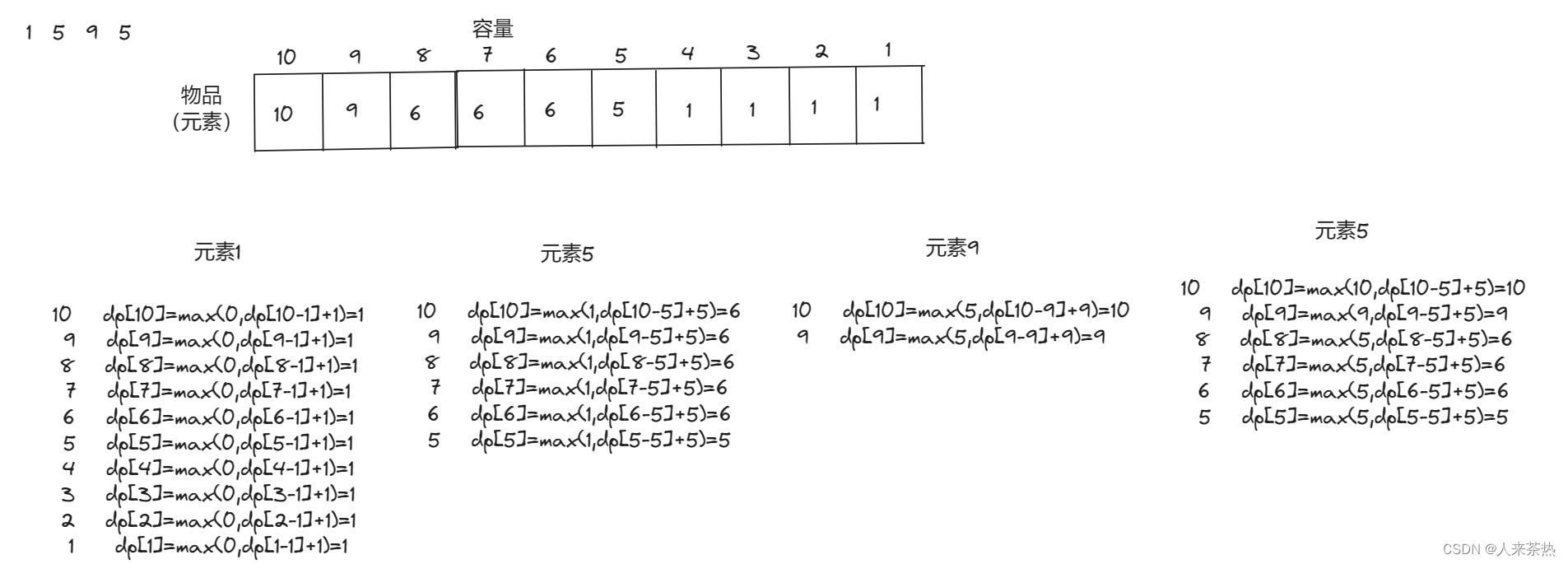
• Next[j] = k :一个用来存放子串返回位置的数组，回溯的位置用字母k来表示。
• 其实就是从匹配失败位置，找到他前面的字符串的最大前后相等子串长度。
• 默认第一个k值为-1(Next[0] = -1),第二个k值为0(Next[1] = 0),我们只需要从第三个k值(Next[2])开始求
• next数组的长度与子串的长度相同

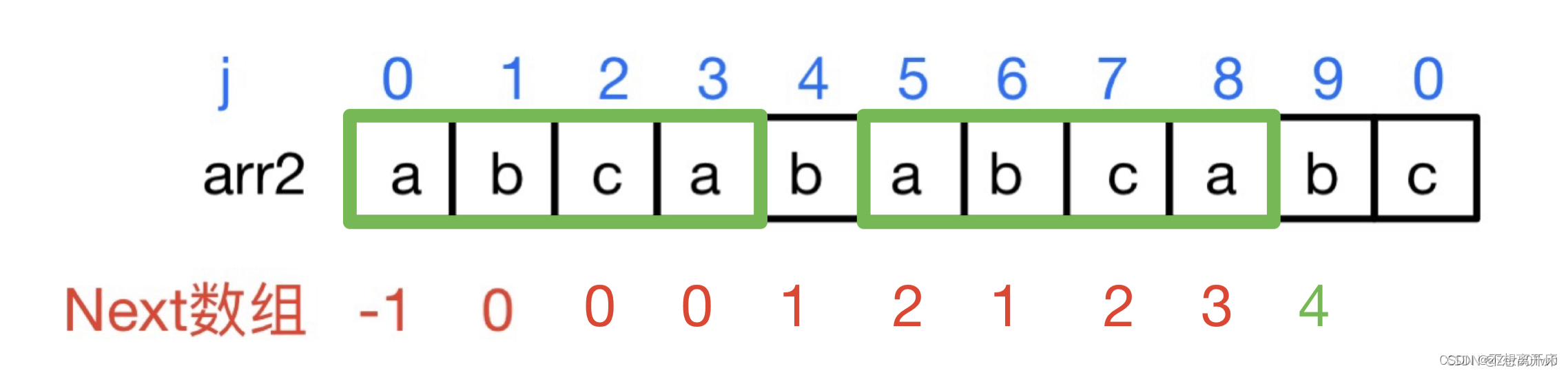
• arr2[k] == arr2[j] ⇒ Next [ j+1 ] = k + 1
  
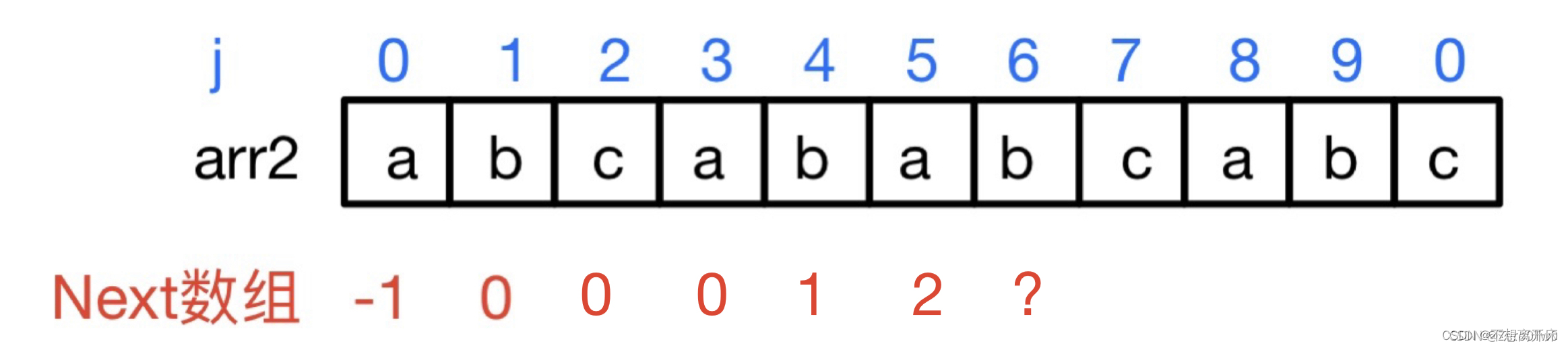
• 此时令j = 5那已知信息就有 arr[j] = ‘a’，Next[j] = k = 2, arr[k] = ‘c’,此时arr[j] != arr[k]

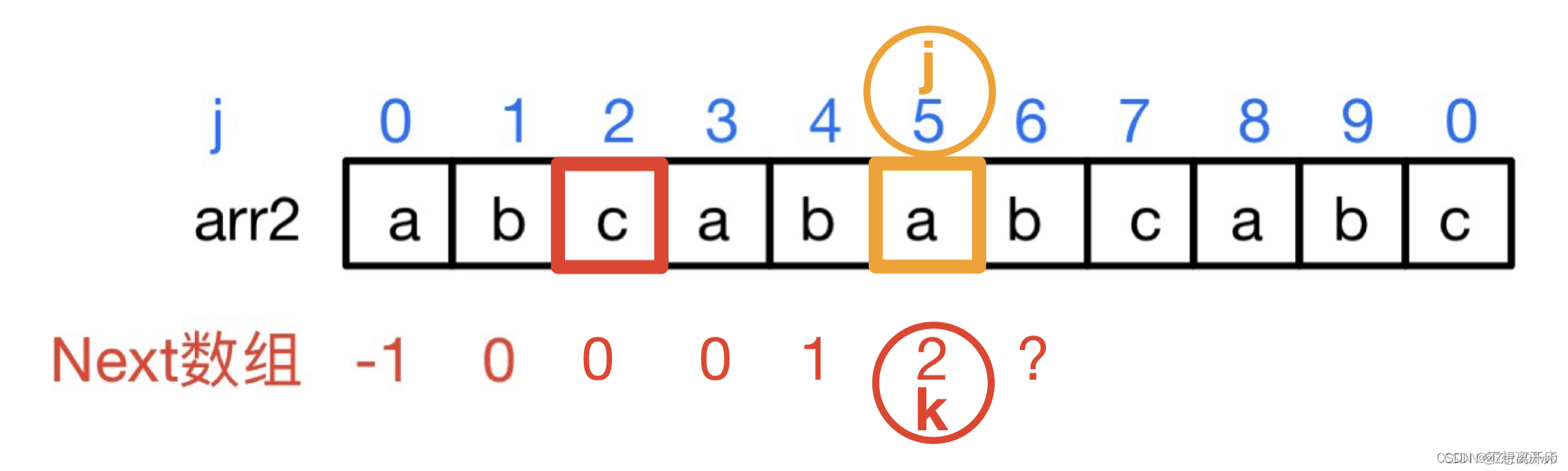
• 那我们就让新的 k = Next[ k ] = 0
• 一直都找不到，那我们此时k肯定回溯到了数组头部，即k = - 1处，那我们就停止回溯， Next [ j + 1 ] = k + 1 ⇒ Next [ j + 1] = 0

#include<stdio.h>
#include<string.h>
 //获得Next数组
void GetNext(int* Next, const char* arr2)           //传入Next数组地址，传入子串首地址
{
    //初始已知项 j = 1
	int j = 1;
	//i从2开始求									
	int i = j + 1;
	//此时k为0								
	int k = 0; 
	                                     
	//子串长度
	int len2 = strlen(arr2);     
	                   
	//Next数组前两个默认值
	Next[0] = -1;									
	Next[1] = 0;
	
	while (i < len2)                                
	{
		if ((k == -1) || arr2[k] == arr2[i - 1])	
		{
			Next[i] = k + 1;
			k = k + 1;                              
			i++;                                    
		}
		else
		{
			k = Next[k];							
		}
	}
}
 
 //KMP算法
int KMP(char* arr1, char* arr2)
{
	int i = 0;											
	int j = 0;                                          
	
	int len1 = strlen(arr1);
	int len2 = strlen(arr2);
	
	int* Next = (int*)malloc(len2 * sizeof(int));       //为Next数组开辟一个与子串一样长的 
                                                        //空间
                                                        
	//借用Next函数得到Next数组的内容
	GetNext(Next, arr2);                                

	if (len1 == 0 && len2 == 0 || len2 == 0) return 0;
	else if (len1 == 0 || len2 > len1) return -1;	
		
    //当arr1和arr2都没走到尽头                                                    
	while (i < len1 && j < len2)						
	{
		if (arr1[i] == arr2[j])
		{
			i++;
			j++;
		}
		else
		{
		    //j回溯
			j = Next[j];						        
		}
	}
	
    //子串全部找到了
	if (j >= len2)
		return i - j;							        
                                                        //开始匹配时的位置
	return -1;											//否则就是主串走到尽头，代表没找到
}
 
int main()
{
	char arr1[] = "abababcabc";                    
	char arr2[] = "abcabc";
	char pos;
	pos = KMP(arr1, arr2);
	printf("%d", pos);
}

优化

先来看一个例子:
主串s=“aaaaabaaaaac”
子串t=“aaaaac”

这个例子中当‘b’与‘c’不匹配时应该‘b’与’c’前一位的‘a’比,这显然是不匹配的。'c’前的’a’回溯后的字符依然是‘a’。

我们知道没有必要再将‘b’与‘a’比对了，因为回溯后的字符和原字符是相同的，原字符不匹配，回溯后的字符自然不可能匹配。但是KMP算法中依然会将‘b’与回溯到的‘a’进行比对。这就是我们可以改进的地方了。我们改进后的next数组命名为：nextval数组。

KMP算法的改进可以简述为：
如果a位字符与它next值指向的b位字符相等，则该a位的nextval就指向b位的nextval值，如果不等，则该a位的nextval值就是它自己a位的next值。

void GetNextval(SqString t,int nextval[])  
//由模式串t求出nextval值
{
	int j=0,k=-1;
	nextval[0]=-1;
   	while (j<t.length) 
	{
       	if (k==-1 || t.data[j]==t.data[k]) 
		{	
			j++;k++;
			if (t.data[j]!=t.data[k]) 
				nextval[j]=k;
           	else  
				nextval[j]=nextval[k];
       	}
       	else  k=nextval[k];    	
	}
}