代码随想录算法训练营 ---第四十九天

news2024/9/24 9:18:38

前言：

今天是买卖股票的最佳时机系列，本系列之前在学习贪心思想时做过一些。

第一题：

简介：

本题在读题时我们要注意到几个细节

1.本题股票买卖只有一次。2.我们要在最低点买股票，在最高点卖股票。

我的思路：

dp[i]含义：在第0天到第i天的最大利益。本题我的思路是不断更新最低点，然后与前一天进行比较那天利益高，这样就保持第0天到第i天的利益。但是此思路只适用于本题目。比较好理解。

int maxProfit(vector<int>& prices) {
        vector<int> dp(prices.size(),0);
        int max1 =prices[0];
        for(int  i=1;i<prices.size();i++){
            dp[i] =max(prices[i] - max1,dp[i-1]);
            if(max1>prices[i]){
                max1 = prices[i];
            }
        }
        if(dp.back()<=0)return 0;
        return dp.back();
    }

题解思路：

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[i][0] 表示第i天持有股票所得最多现金我们假设刚开始的现金为0，那么加入第i天持有股票（包含当天买入和前几天就买入了）现金就是 -prices[i]，这是一个负数。

dp[i][1] 表示第i天不持有股票（包含以前就卖出去了和当天卖出去）所得最多现金

2 .确定递推公式

如果第i天持有股票即dp[i][0]，那么可以由两个状态推出来

第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]

那么dp[i][0]应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i]);

如果第i天不持有股票即dp[i][1]，也可以由两个状态推出来

第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]，同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

3.dp数组如何初始化

由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出其基础都是要从dp[0][0]和dp[0][1]推导出来。那么dp[0][0]表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，

所以dp[0][0] -= prices[0];

dp[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0;

4.确定遍历顺序

从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历。

5.举例推导dp数组

以示例1，输入：[7,1,5,3,6,4]为例，dp数组状态如下：

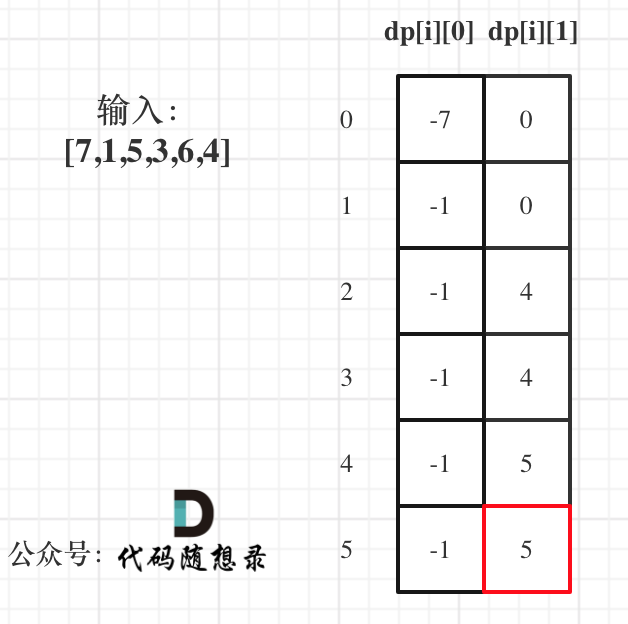
121.买卖股票的最佳时机

dp[5][1]就是最终结果。

为什么不是dp[5][0]呢？

因为本题中不持有股票状态所得金钱一定比持有股票状态得到的多！

代码实现：

  int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if (len == 0) return 0;
        vector<vector<int>> dp(len, vector<int>(2));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
        }
        return dp[len - 1][1];
    }

注：我认为本题看题解思路一定要时刻提醒自己dp二维数组的含义，否则很容易混乱。然后我们要知道，本题只需要买卖一次，所以dp[i][0]可以得到买入股票花费最少的点。dp[i][1]可以得到卖出股票利益最大的点。

第二题：

简介：

本题和上一题不同的点在于本题股票可以多次买卖，没有限制。我认为第一次做的同学先去看贪心思想的解法，再来看动态规划的解法。

两题代码上唯一的不同点

此不同点出现的原因在于本题不限制股票买卖次数所以我们买入股票时手里可能有钱。

代码实现：

贪心思想：

int maxProfit(vector<int>& prices) {
        int  result=0;
         for(int i=0;i<prices.size();i++){
             if(i+1 == prices.size())continue;
             if(prices[i+1]-prices[i]>0){
                 result += prices[i+1]-prices[i];
             }
         }
         return result;
    }

动态规划：

我的动态规划（不知道算不算感觉有点像贪心的思想）：

 int maxProfit(vector<int>& prices) {
       vector<int> dp(prices.size(),0);
       for(int i=1;i<prices.size();i++){
           if(prices[i]-prices[i-1]>0){
               dp[i] = prices[i]-prices[i-1]+dp[i-1];
           }else{
               dp[i] +=dp[i-1];
           }
       }
       return dp.back();
    }

题解：

 int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(len, vector<int>(2, 0));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和121. 买卖股票的最佳时机唯一不同的地方。
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return dp[len - 1][1];
    }