贪心算法
在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

过程：
建立数学模型来描述问题；
把求解的问题分成若干个子问题；
对每一子问题求解，得到子问题的局部最优解；
把子问题的解局部最优解合成原来解问题的一个解。

贪心与动态规划

联系：均由局部最优解来推导全局最优解，问题都具有最优子结构性质。

区别： 贪心只从当前的选择中，构造某种最优解。 动态规划综合考虑之前状态和当前的选择，决定当前状态的最优解。

背包问题

首先计算每种物品单位重量的价值Pi = Vi / Wi

然后，依贪心选择策略，将尽可能多的单位重量价值最高的物品装入背包。若将这种物品全部装入背包后，背包内的物品总重量未超过C，则选择单位重量价值次高的物品并尽可能多地装入背包。

依此策略一直地进行下去，直到背包装满为止。

void Knapsack(int n,float M,float v[],float w[],float x[])
{  //n为物品总数，M为总容量
       Sort(n,v,w);
       int i;
       for (i=1;i<=n;i++) x[i]=0;
       float c=M;  // 剩余的容量
       for (i=1;i<=n;i++) {
          if (w[i]>c)  break;
          x[i]=1;
          c-=w[i];
          }
       if (i<=n) x[i]=c/w[i];
}

算法knapsack的主要计算时间在于将各种物品依其单位重量的价值从大到小排序。因此，算法的计算时间上界为O（nlogn）。

活动安排问题

template<class Type>
void GreedySelector(int n, Type s[], Type f[], bool A[])
{ // s数组存储活动起始时间，f数组存储活动结束时间，且各活动按结束时间已按非减序排列；A数组存储被选中的活动。
       A[1]=true;  // 选择活动1（结束最早的活动）
       int j=1; // j记录最近一次被选中的活动
       for (int i=2;i<=n;i++) {
          if (s[i]>=f[j]) { A[i]=true; j=i; }
          else A[i]=false;
          } // 每次总是选择具有最早完成时间的相容活动加入集合A中
}

最优装载问题

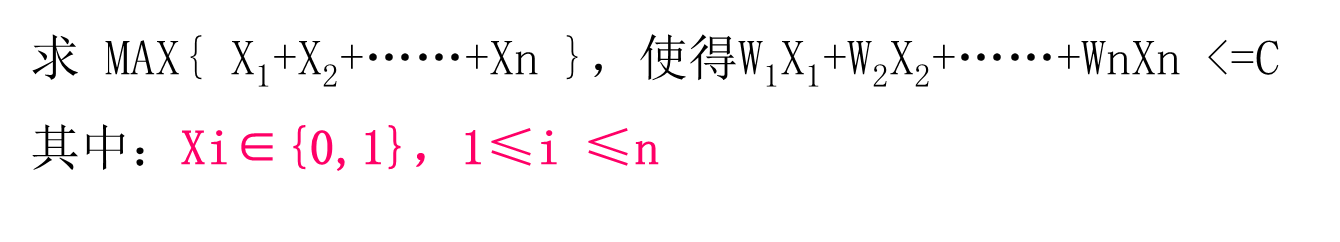
int  Loading(int x[ ],  int w[ ],  int C,  int n) // C为轮船剩余载重量
{    int *t= new  int[n+1];
     Sort(w, t, n);    
     for(i=1;i<=n; ++i)   x[i]=0;
     for(i=1;   w[t[i]]<=C&& i<=n;  ++i)
         {   x[t[i]]=1;  C -= w[t[i]];    }   
}

删数问题

每次对正整数a进行“从最高位向最低位”的扫描，若当前位比后一位大，则删除当前位，后续的数字前移。

while (k > 0)
{
  int i = 0;
  while (i <= len && a[i] <= a[i+1])
      i++;            
  for (int j = i; j <= len; j++) 
      a[j] = a[j+1];
   k--;
   len--;
}

最优服务次序