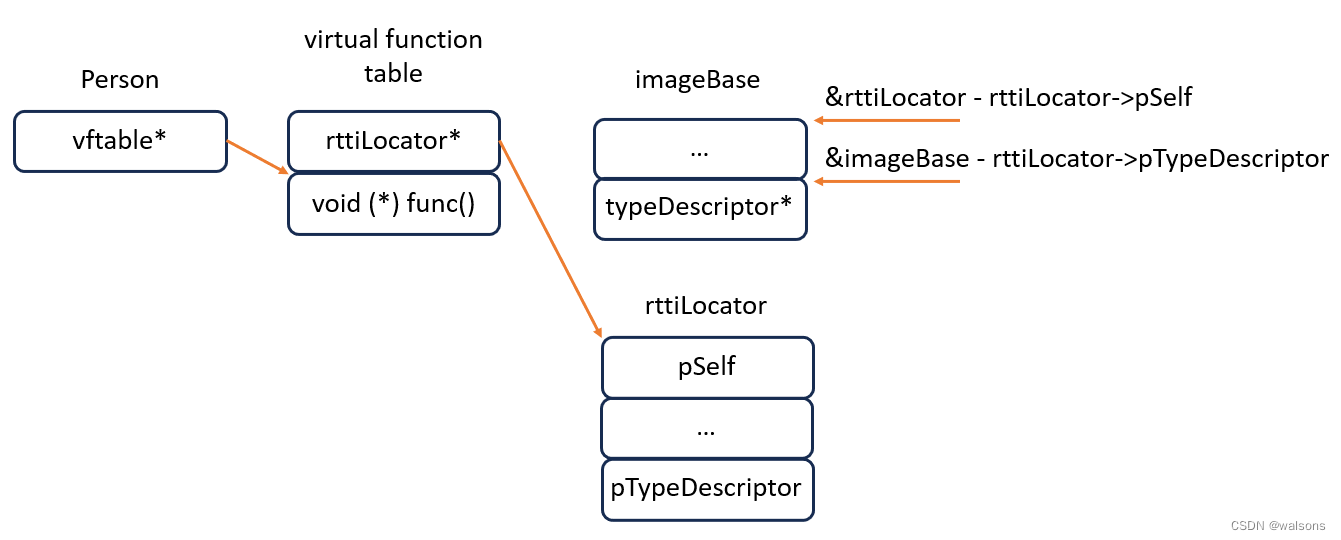
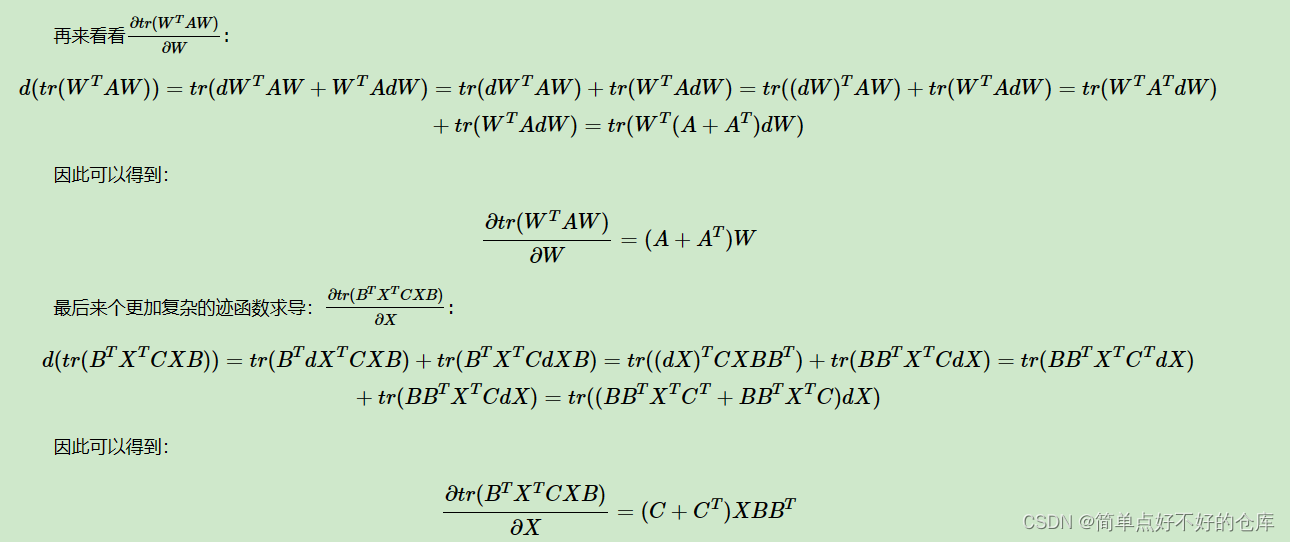机器学习中矩阵向量求导的概念是什么？

在机器学习中，矩阵向量求导的概念主要涉及对函数中的矩阵或向量参数进行求导运算。这种求导运算可以帮助我们了解函数值随参数的变化情况，进而应用于优化算法中。具体来说，当损失函数是一个关于模型参数（通常表示为矩阵或向量）的函数时，我们需要计算损失函数关于模型参数的导数，即梯度。这个梯度可以用来更新模型参数，使得损失函数值降低，从而提高模型的性能。

矩阵向量求导可以分为多种类型，包括向量对标量的求导、向量对向量的求导、以及矩阵对矩阵的求导等。每种类型都有其特定的定义和计算规则。例如，向量对标量的求导实际上是对向量中的每个分量分别对标量进行求导，并将结果按向量形式排列。而矩阵对矩阵的求导则更为复杂，涉及到矩阵间的逐元素求导和排列方式等问题。

在机器学习的实际应用中，我们通常使用数值方法来计算雅可比矩阵和梯度等，例如使用有限差分法或反向传播算法等。这些方法可以帮助我们有效地计算梯度并更新模型参数，从而实现模型的优化和训练。

求导的布局？

矩阵求导的两种布局分别是分子布局（Numerator Layout）和分母布局（Denominator Layout）。

大牛链接

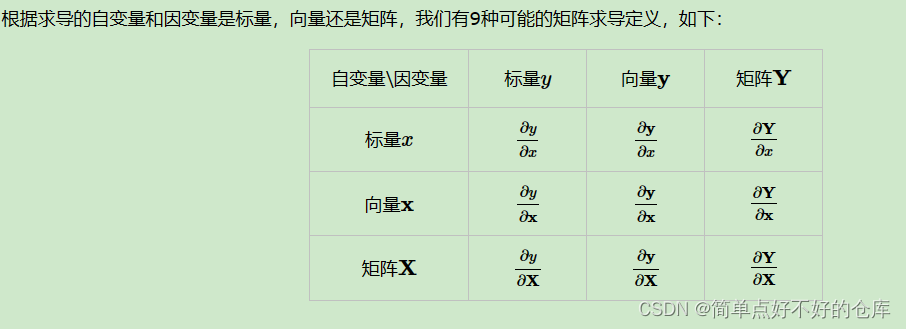
全文就这句最重要
总而言之，所谓的向量矩阵求导本质上就是多元函数求导，仅仅是把把函数的自变量，因变量以及标量求导的结果排列成了向量矩阵的形式，方便表达与计算，更加简洁而已。

所有的都可对标量的求导，然后根据布局构成最终的结果。

对标量求导

• 分子布局，我们求导结果的维度以分子为主，对于标量求导，结果的维度和分子的维度是一致的。也就是说，如果向量y是一个m维的列向量，那么求导结果也是一个m维列向量。如果如果向量y是一个m维的行向量，那么求导结果也是一个m维行向量。
• 分母布局，我们求导结果的维度以分母为主，对标量求导，如果向量y是一个m维的列向量，那么求导结果是一个m维行向量。如果如果向量y是一个m维的行向量，那么求导结果是一个m维的列向量向量.

上面的是对标量的求导，那么对向量的求导呢？

对向量求导

参考

如何记住这么多的求导？如何推到没见过的呢？

有三种方法

1 定义法

逮着向量中的标量进行求导：

总结一下, 转化为对每一标量求导，然后进行布局。

大家自己推一推

巩固一下

常见的规则

2 微分法

这个就有点不显而易见了

涉及到 trace了，背景知识如下

举例背诵

终于背完了，那么开始

自己趁热打铁一下：

3 链式法则法

趁热打铁一下：

下面的也可自己推导一下：