定义:平衡二叉树是一棵二叉排序树,或者为空,或者满足以下条件:
1)左右子树高度差的绝对值不大于1;
2)左右子树都是平衡二叉树。
平衡因子:左子树的高度减去右子树的高度,显然,在平衡二叉树中,每个结点的平衡因子的值为-1,0或1。
在Java中,构造平衡二叉树通常涉及到 AVL 树(Adelson-Velsky and Landis tree)的实现。AVL 树是一种自平衡二叉搜索树,它通过保持每个节点的左右子树高度差不超过1来保持平衡。
插入操作的可能情况:
LL型:新插入结点在A的左孩子(L)的左子树(L)中;
LR型:新插入结点在A的左孩子(L)的右子树(R)中;
RL型:新插入结点在A的右孩子(R)的左子树(L)中;
RR型:新插入结点在A的右孩子(R)的右子树(R)中。
LL型:右旋是指将一个节点的左子树变为其父节点,同时该节点成为其左子树的右子节点。右旋用于解决左子树过深的情况。
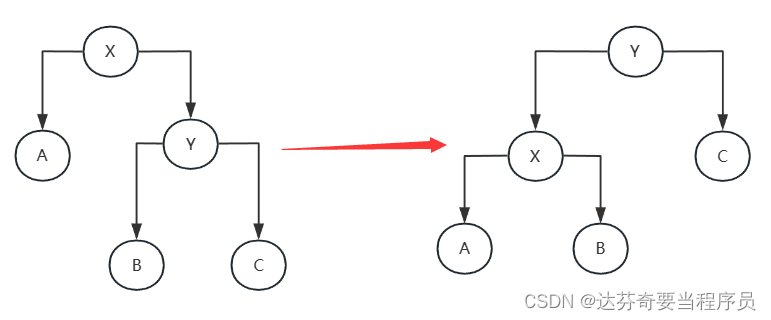
LR型:右左旋是先对当前节点的右子树进行右旋,然后再对当前节点进行左旋。这用于解决右子树的左子树过深的情况。
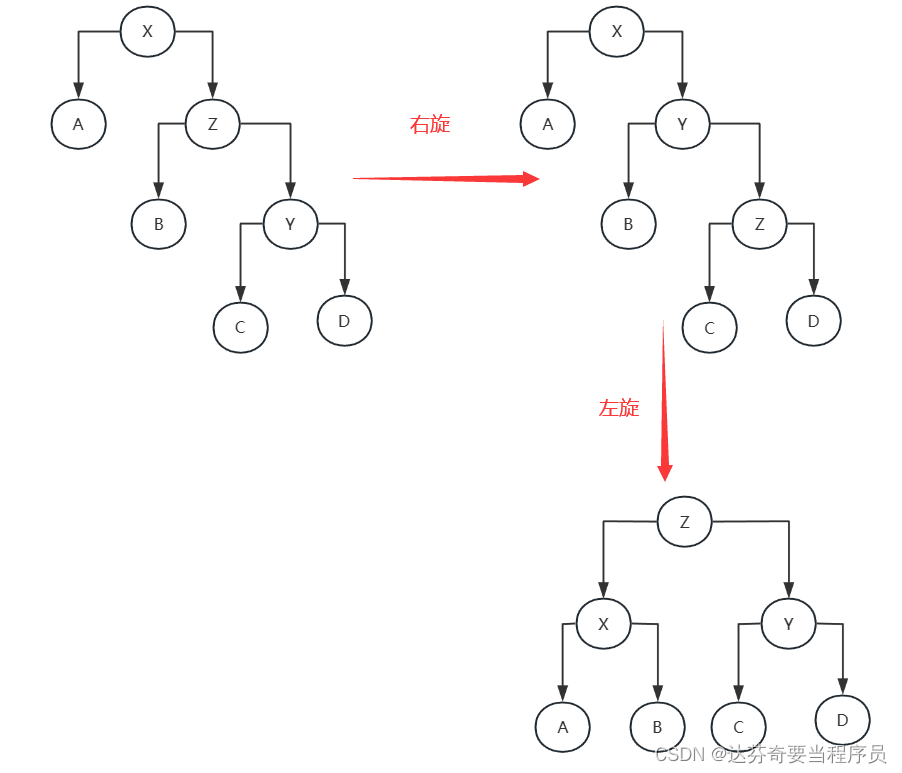
RL型:左右旋是先对当前节点的左子树进行左旋,然后再对当前节点进行右旋。这用于解决左子树的右子树过深的情况。
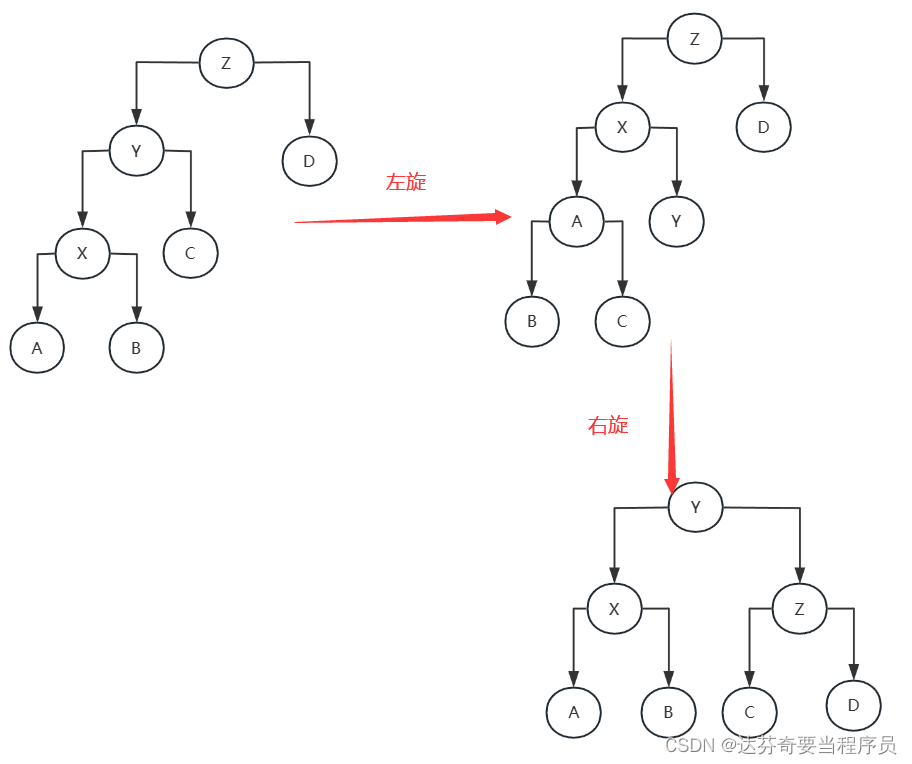
RR型:左旋是指将一个节点的右子树变为其父节点,同时该节点成为其右子树的左子节点。左旋用于解决右子树过深的情况。
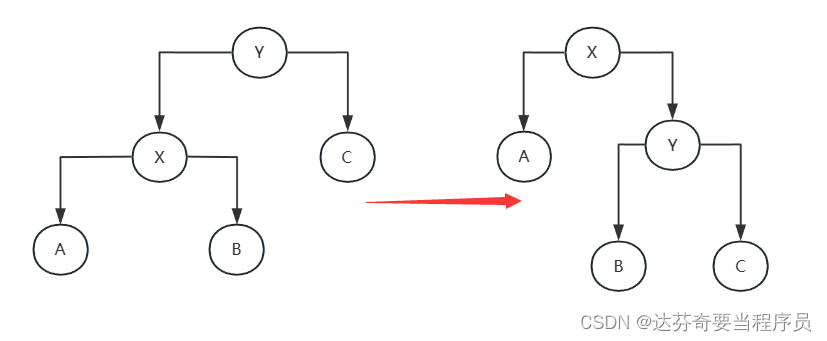
以上都是基于左旋和右旋实现的,那么接下来我们构建左旋和右旋的方法以及插入数据对树结构所做操作:
对一组数据构建平衡二叉树:10、5、20、13、17、4
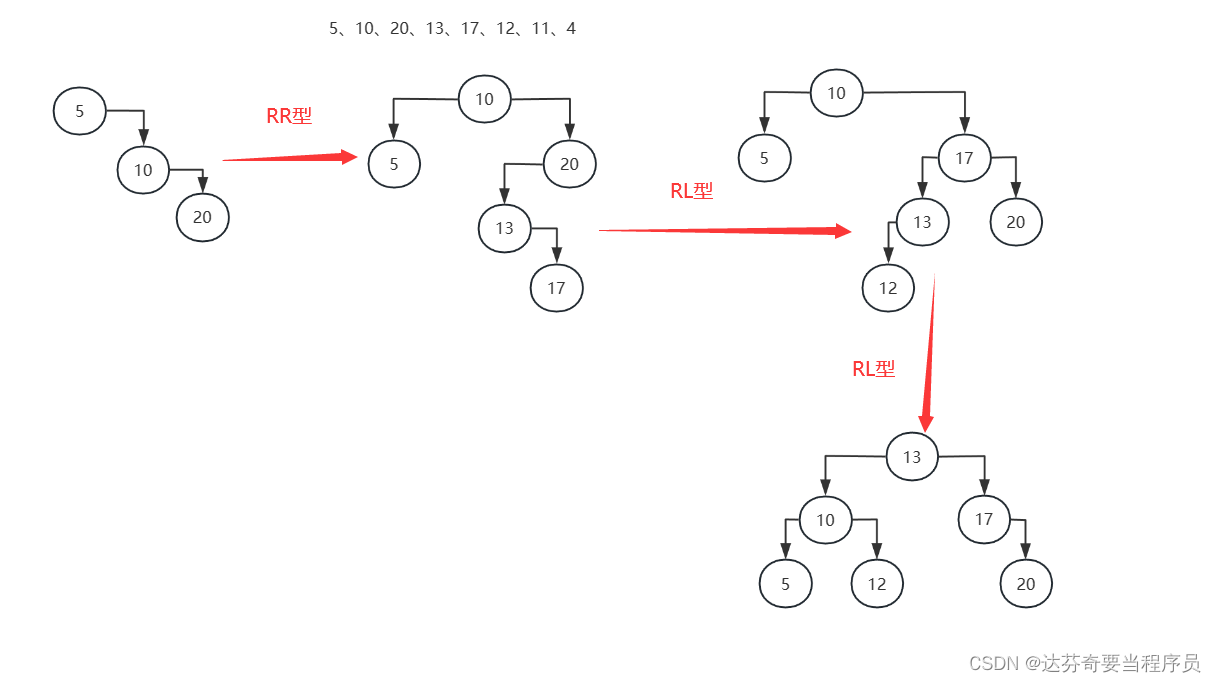
现在我们利用代码实现。
首先,需要创建一个 TreeNode 类,这个类除了包含节点值之外,还需要保存节点的高度:
public class TreeNode {
int val;
int height;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
this.height = 1; // 初始高度为1
}
}然后,创建一个 AVL 树的实现类,其中包括插入操作和平衡操作:
public class AVLTree {
private TreeNode root;
// 获取节点的高度
private int height(TreeNode node) {
if (node == null) {
return 0;
}
return node.height;
}
// 获取平衡因子
private int getBalance(TreeNode node) {
if (node == null) {
return 0;
}
return height(node.left) - height(node.right);
}
// 更新节点的高度
private void updateHeight(TreeNode node) {
if (node != null) {
node.height = Math.max(height(node.left), height(node.right)) + 1;
}
}
// 右旋转
private TreeNode rightRotate(TreeNode y) {
TreeNode x = y.left;
TreeNode T2 = x.right;
// 执行旋转
x.right = y;
y.left = T2;
// 更新高度
updateHeight(y);
updateHeight(x);
return x;
}
// 左旋转
private TreeNode leftRotate(TreeNode x) {
TreeNode y = x.right;
TreeNode T2 = y.left;
// 执行旋转
y.left = x;
x.right = T2;
// 更新高度
updateHeight(x);
updateHeight(y);
return y;
}
// 插入节点
public TreeNode insert(TreeNode node, int val) {
if (node == null) {
return new TreeNode(val);
}
// 执行标准的BST插入
if (val < node.val) {
node.left = insert(node.left, val);
} else if (val > node.val) {
node.right = insert(node.right, val);
} else {
// 重复的值不被允许
return node;
}
// 更新节点的高度
updateHeight(node);
// 获取平衡因子
int balance = getBalance(node);
// 左子树的左侧插入,需要右旋转
if (balance > 1 && val < node.left.val) {
return rightRotate(node);
}
// 右子树的右侧插入,需要左旋转
if (balance < -1 && val > node.right.val) {
return leftRotate(node);
}
// 左子树的右侧插入,需要先左旋转再右旋转
if (balance > 1 && val > node.left.val) {
node.left = leftRotate(node.left);
return rightRotate(node);
}
// 右子树的左侧插入,需要先右旋转再左旋转
if (balance < -1 && val < node.right.val) {
node.right = rightRotate(node.right);
return leftRotate(node);
}
return node;
}
// 插入新节点,外部调用该方法
public TreeNode insert(int val) {
root = insert(root, val);
//返回根节点
return root;
}
}定义一个BinaryTreePrinter类,使用深度优先搜索来打印二叉树:
public class BinaryTreePrinter {
public static void printTree(TreeNode root) {
printTreeHelper(root, 0);
}
private static void printTreeHelper(TreeNode node, int depth) {
if (node == null) {
return;
}
// 打印右子树,使其显示在上方
printTreeHelper(node.right, depth + 1);
// 打印当前节点
for (int i = 0; i < depth; i++) {
System.out.print(" "); // 每层缩进四个空格
}
System.out.println(node.val);
// 打印左子树,使其显示在下方
printTreeHelper(node.left, depth + 1);
}
}在测试类Test中创建了一个 AVLTree 实例,并调用其方法来操作 AVL 树:
public class Test {
public static void main(String[] args) {
AVLTree avlTree =new AVLTree();
// 构造一棵平衡二叉树
avlTree.insert(5);
avlTree.insert(10);
avlTree.insert(20);
avlTree.insert(13);
avlTree.insert(17);
TreeNode root=avlTree.insert(12);
System.out.println("平衡二叉树高度:"+root.height);
BinaryTreePrinter.printTree(root);
}
}根节点为13,结果如下:

与构建结果相同。