目录
动态规划算法优化
一维 —> 常量
leetcode70题.爬楼梯
二维 —>一维
leetcode62题.不同路径
动态规划算法优化
优化的原则如下:
1、把一维数组优化为常量
2、把二维数组优化为一维
优化的核心:画图辅助
一维 —> 常量
leetcode70题.爬楼梯
70. 爬楼梯 - 力扣(LeetCode)
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶提示:
1 <= n <= 45
当我们画一个跳楼梯的数组时我们会发现,dp[i]的值只跟dp[i - 1]和dp[i - 2]的值有关,所以我们可以用a,b,c三个变量动态保存dp[i - 1]和dp[i - 2]的值。这样的代码空间复杂度会大大降低。
class Solution {
/*动态规划三部曲
第一步:
dp[i]数组含义:表示爬到第i个台阶时,一共有dp[i]种爬法。
第二步:求关系时
dp[i] dp[i-1] dp[i-2]
要么是从i-1跳上来 要么就是从i-2跳上来的
dp[i] = dp[i-1] + dp[i-2];
第三步:初始值
dp[0] = 1;
dp[1] = 1
dp[2] = 2;
*/
public int climbStairs(int n) {
if(n <= 1){
return 1;
}
//int[] dp = new int[n+1];
int a = 1;
int b = 1;
int c = 1;
for(int i = 2; i <= n; i++){
c = a + b;
a = b;
b = c;
}
return c;
}
}
二维 —>一维
leetcode62题.不同路径
62. 不同路径 - 力扣(LeetCode)
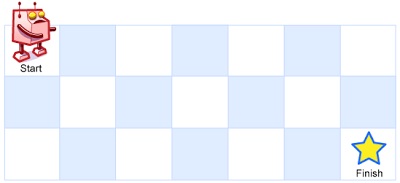
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
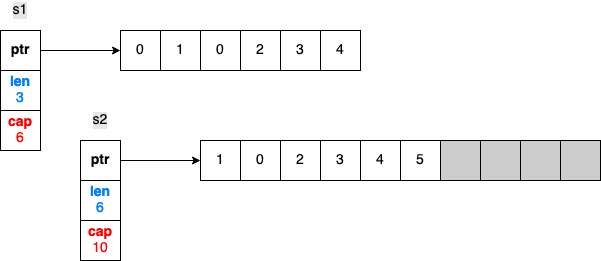
由dp[i][j] = dp[i-1][j] + dp[i][j-1]画一个二维数组可知,我们计算第i行时只用到了i - 1这一行的数据,所以我们只需要动态利用i - 1这一行的数据就可以了。转化为dp[j] = dp[j] + dp[j-1] 这种方式也叫滚动数组。
/*
二维的思路 O(m * n)
1、定义:dp[i][j]:到达[i, j]时,一共有dp[i, j]个路径
2、关系式:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
3、初始化
dp[0][0...m - 1] = 1
dp[0...n - 1][0] = 1
*/
//一维的 O(N)
class Solution {
public int uniquePaths(int m, int n) {
//数组一行一行计算应该保存一列的值
int[]dp = new int[n];
// 初始值
//最左边的一列
for(int i = 0; i < n; i++){
dp[i] = 1;
}
for(int i = 1; i < m; i++){
//下面这个for循环表示计算第i行
dp[0] = 1;
for(int j = 1; j < n; j++){
dp[j] = dp[j] + dp[j-1];
}
}
return dp[n-1];
}
}