难度
困难
题目
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n_ _皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

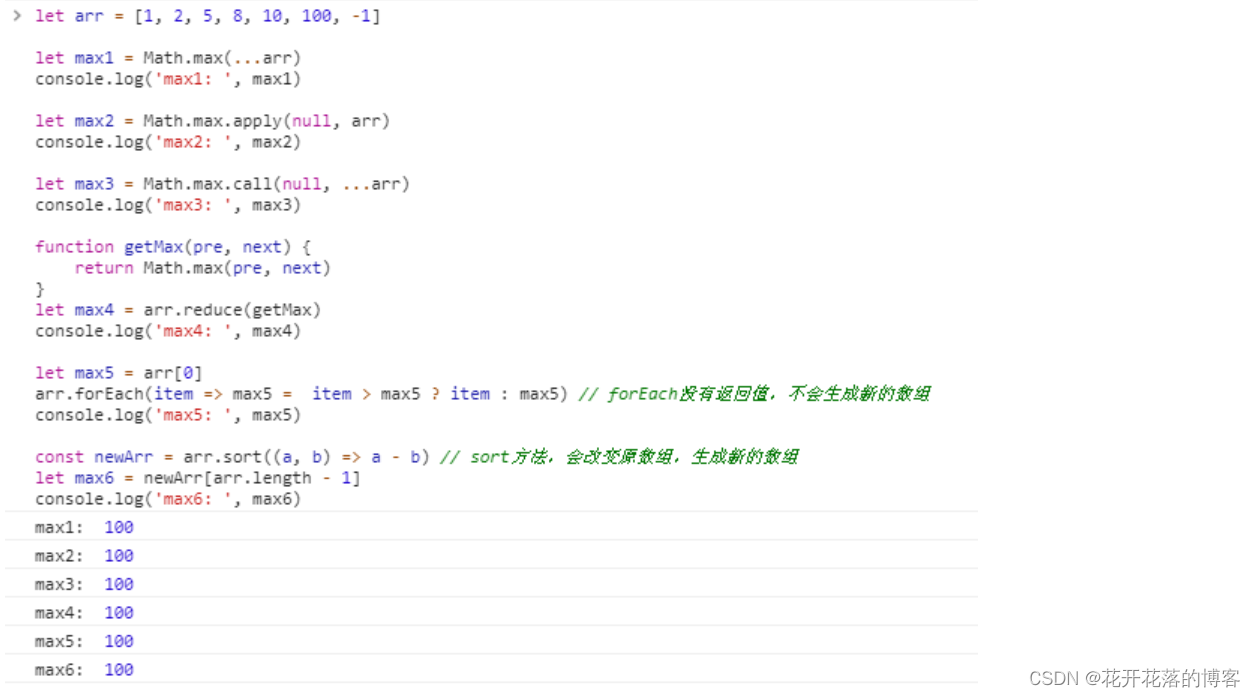
示例 1:
输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
思路
N 皇后问题是一个经典的回溯算法问题,要求在 N×N 的棋盘上放置 N 个皇后,使得它们互相不能攻击(即不能在同一行、同一列或同一斜线上),N 皇后问题的一种解题思路,采用回溯算法:
- 初始化一个 n * n的棋盘,默认都为0,表示未放棋,初始化三个集合,分别记录列,正对角线,反对角线是否放置棋。
- 递归地尝试每一行,并且横向遍历每一列,检查当前位置是否符合规则,即:
- 检查该点所在的列、正对角线、反对角线是否已经放置棋,如果未放置则该点可以放置棋。
- 正对角线判断规则,从左上到右下 同一条斜线上的每个位置满足行下标与列下标之差相等
- 反对角线判断规则,从右上到左下 同一条斜线上的每个位置满足行下标与列下标之和相等
- 当递归的行数达到边界时,退出递归。
代码
from typing import List
class Solution:
def solveNQueens(self, n):
self.index = 1
self.n = n
# 初始化 n * n的棋盘,默认都为0,未放棋
self.chessboard = [[0] * self.n for i in range(self.n)]
# 记录已经放了棋的列
self.col = set()
# 记录已经放了棋的正对角线
self.d1 = set()
# 记录已经放了棋的反对角线
self.d2 = set()
self.result = []
self.dfs(0)
def dfs(self, row):
# 检查每一行能否放棋
if row >= self.n:
# 当行数到达边界时,打印结果
print(self.index, '----------------------')
self.printq()
self.index += 1
self.result.append(self.chessboard)
return self.result
# 扫描每一列元素
for col in range(self.n):
# d1 表示 从右上到左下 同一条斜线上的每个位置满足行下标与列下标之和相等
# d2 表示 从左上到右下 同一条斜线上的每个位置满足行下标与列下标之差相等
d1, d2 = col + row, col - row
# 检查列是否被占用
if col in self.col:
continue
# 检查正对角线是否被占用 列-行
if d1 in self.d1:
continue
# 检查反对角线是否被占用 列+行
if d2 in self.d2:
continue
# 放置皇后
self.chessboard[row][col] = 1
# 标记
self.col.add(col)
self.d1.add(d1)
self.d2.add(d2)
# 纵向遍历,检查下一行
self.dfs(row + 1)
# 回溯
self.col.remove(col)
self.d1.remove(d1)
self.d2.remove(d2)
self.chessboard[row][col] = 0
def printq(self):
for i in self.chessboard:
x = []
for j in i:
if j == 1:
x.append('Q ')
else:
x.append('* ')
print(''.join(x))
def prt(data):
for line in data:
print(line)
# 第二种解法
def NQ(data, row, n):
if row == n:
prt(data)
return
# 检查row当前行中所有列
for i in range(n):
# 检查当前节点是否可以放棋
if check_point(data, row, i):
data[row][i] = 1
# 进下一行,中所有的列
NQ(data, row + 1, n)
data[row][i] = 0
def check_point(data, row, col):
# 检查 (row, col) 点的位置是否可以放
n = len(data[0])
# 检查当前点所在的列中,是否已经放了棋
for i in range(row):
if data[i][col] == 1:
return False
# 当前行
for i in range(row):
# 所有列
for j in range(n):
# 检查两个对角线中是否已经放了棋
if i + j == row + col and data[i][j] == 1:
return False
if i - j == row - col and data[i][j] == 1:
return False
return True
def main(n):
data = [[0] * n for _ in range(n)]
NQ(data, 0, n)
if __name__ == '__main__':
s = Solution()
res = s.solveNQueens(4)
# print(res)
main(4)