为什么取名为梳，可能每个梳都有自己的 gap 吧，大梳子 gap 大一点，小梳子 gap 小一点。上一篇我们看到鸡尾酒排序是在冒泡排序上做了一些优化，将单向的比较变成了双向，同样这里的梳排序也是在冒泡排序上做了一些优化。
冒泡排序上我们的选择是相邻的两个数做比较，就是他们的 gap 为 1，其实梳排序提出了不同的观点，如果将这里的 gap 设置为一定的大小，效率反而必 gap=1 要高效的多。
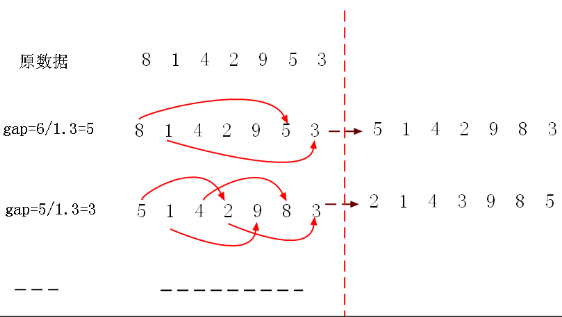
下面我们看看具体思想，梳排序有这样一个 1.3 的比率值，每趟比较完后，都会用这个 1.3 去递减 gap，直到 gap=1 时变成冒泡排序，这种算法比冒泡排序的效率要高效的多，时间复杂度为 O(N2/2p) 这里的 p 为增量，是不是跟希尔排序有点点神似。
比如下面有一组数据: 初始化的 gap=list.count/1.3， 然后用这个 gap 作为数组下标进行跨数字比较大小，前者大于后者则进行交换，每一趟排序完成后都除以 1.3, 最后一直除到 gap=1.

最后我们的数组就排序完毕了，下面看代码：

 using System;
 using System.Collections.Generic;
 using System.Linq;
 using System.Text;
 using System.Xml.Xsl;
 
 namespace ConsoleApplication1
 {
     class Program
     {
         static void Main(string[] args)
         {
             List<int> list = new List<int>() { 8, 1, 4, 2, 9, 5, 3 };
 
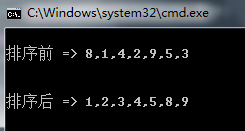
             Console.WriteLine("\n排序前 => {0}\n", string.Join(",", list));
 
             list = CombSort(list);
 
             Console.WriteLine("\n排序后 => {0}\n", string.Join(",", list));
 
             Console.Read();
         }
 
         /// <summary>
         /// 梳排序
         /// </summary>
         /// <param name="list"></param>
         /// <returns></returns>
         static List<int> CombSort(List<int> list)
         {
             //获取最佳排序尺寸： 比率为 1.3
             var step = (int)Math.Floor(list.Count / 1.3);
 
             while (step >= 1)
             {
                 for (int i = 0; i < list.Count; i++)
                 {
                     //如果前者大于后者，则进行交换
                     if (i + step < list.Count && list[i] > list[i + step])
                     {
                         var temp = list[i];
 
                         list[i] = list[i + step];
 
                         list[i + step] = temp;
                     }
 
                     //如果越界，直接跳出
                     if (i + step > list.Count)
                         break;
                 }
 
                 //在当前的step在除1.3
                 step = (int)Math.Floor(step / 1.3);
             }
 
             return list;
         }
     }
 }