目录
- 前言
- 计算零空间 Nullspace
- 特解 Special solutions
- 行最简阶梯矩阵 Reduced row echelon form (rref)
前言
我们定义了矩阵的列空间和零空间,那么如何求得这些子空间呢?本节课的内容即从定义转到算法。
计算零空间 Nullspace
矩阵 A 的零空间即满足 Ax=0 的所有 x 构成的向量空间。
取
A
=
[
1
2
2
2
2
4
6
8
3
6
8
10
]
取A =\begin{bmatrix} 1 & 2 & 2 &2 \\ 2 & 4 & 6 & 8 \\ 3 & 6 & 8 & 10 \end{bmatrix}
取A=
1232462682810
(A 的列空间并不是线性无关的。)无论矩阵 A 是否可逆,我们都采用消元法作为计算零空间的算法。
对于矩阵 A 进行“行操作”并不会改变 Ax=b 的解,因此也不会改变零空间。(但是会改变列空间。)此处不需要应用增广矩阵,因为等号右侧的向量 b=0。
第一步消元得到:
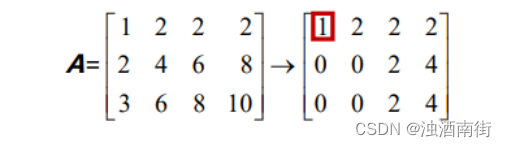
第二列没有主元,因此主元二是第二行第三列的 2。
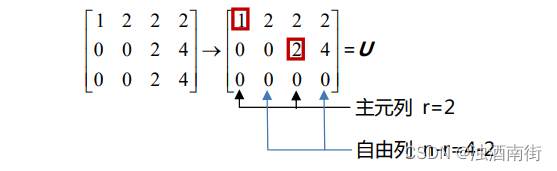
矩阵 U 为梯形矩阵。其第三行变为零,是因为第三行的行向量本身就是第一行和第二行行向量的线性组合。
矩阵的秩(rank)就是矩阵的主元的个数。本例中矩阵 A 和 U 的秩均为 2。矩阵中包含主元的列为主元列(pivot column),不包含主元的列称为自由列(free column)。
特解 Special solutions
当我们将系数矩阵变换为上三角阵 U 时,就可以用回代求得方程 Ux=0 的解。本例中,包含主元的矩阵第 1 列和第 3 列为主元列,而不包含主元的第 2 列和第 4列为自由列。对自由变量(free variable)x2和 x4我们可以进行赋值。例如令 x2=1而 x4=0。则有

矩阵 A 的零空间就是这些“特解”向量的线性组合所构成的向量空间。 矩阵的秩 r 等于其主元列的数目,因此自由列的数目就等于 n-r,即列的数目减去主元列的数目。这个数值等于特解的数目和零空间的维数。
行最简阶梯矩阵 Reduced row echelon form (rref)
通过继续消元我们可以将矩阵 U 转变为行最简阶梯矩阵形式 R,其中主元为 1,而主元列除主元外皆为 0。在 Matlab 中用命令 rref(A)实现这一过程。
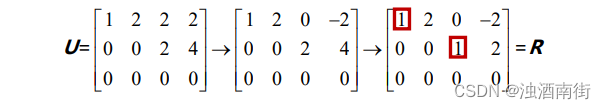
在矩阵中主元行和主元列的交汇处存在一个单位阵。通过“列交换”,可以将矩阵 R 中的主元列集中在左侧,从而在左上角形成这个单位阵,而将自由列集中在矩阵的右侧。如果矩阵 A 中的某些行是线性相关的,则在矩阵 R 的下半部分就会出现一些完全为 0 的行向量。

这里的 I 是一个 r x r 的方阵。F 即自由列消元后组成的部分。