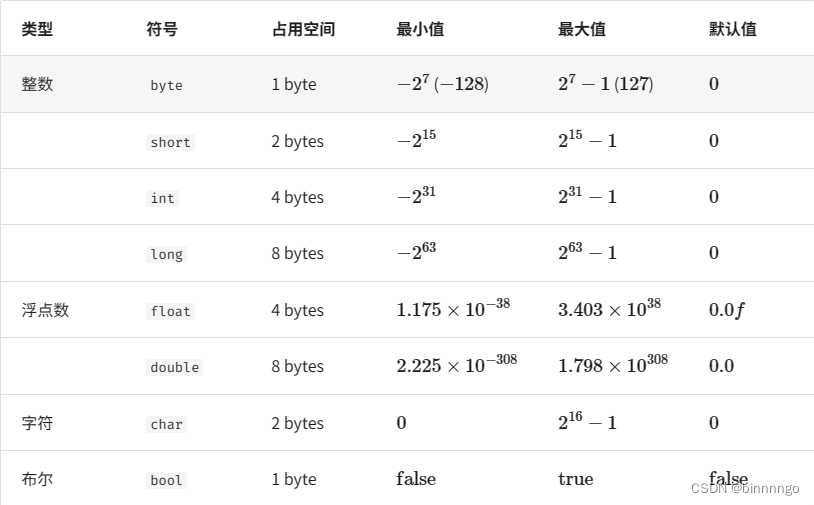
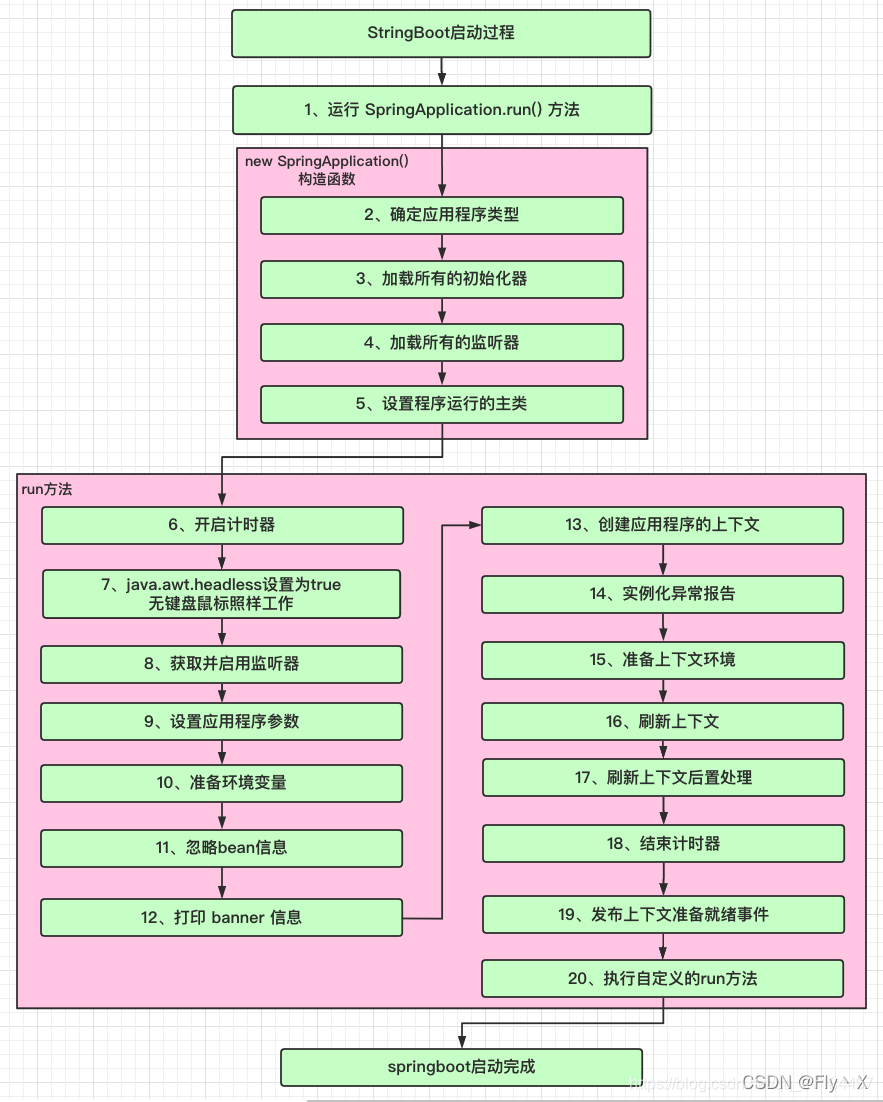
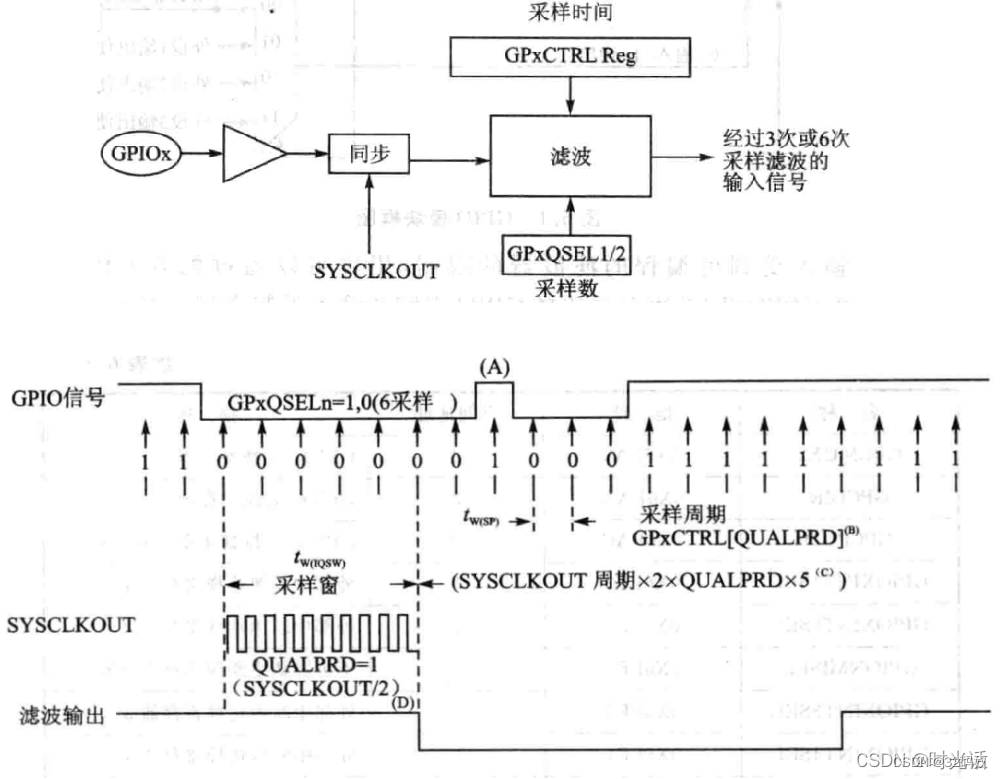
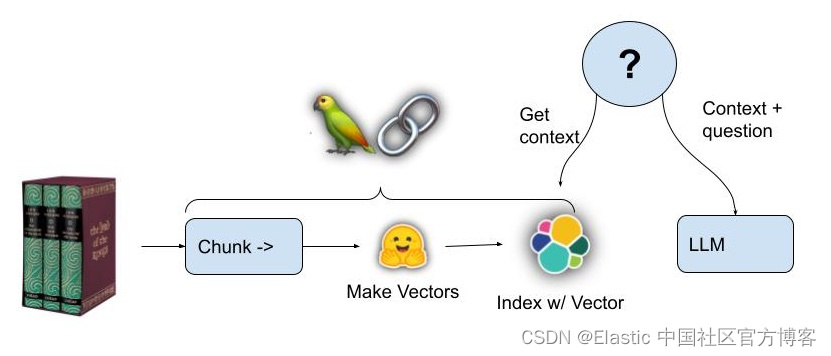
例一

设某客观现象可用$X$=($X_1$，$X_2$，$X_3$)’ 来描述，在因子分析时，从约相关阵出发计算特征值为${\lambda }_1$=1.754，${\lambda }_2$=1，${\lambda }_3$=0.255。由于（${\lambda }_1$+${\lambda }_2$）/（${\lambda }_1$+${\lambda }_2$+${\lambda }_3$）> 85%，所以找前两个特征值所对应的公共因子即可，又知${\lambda }_1$，${\lambda }_2$对应的正则化特征向量分别为（0.707，-0.316，0.632)’ 及(0，0.899，0.447)’ ，要求：
（1）计算因子载荷矩阵A，并建立因子模型。
（2）计算共同度$h_i^2$（i=1，2，3）。
（3）计算第一公因子对X的贡献。

---

解：
（1）根据题意，只需要找前两个特征值对应的公共因子，因此：
STEP1A=($u_1$，$u_2$) $\left[\begin{array}{cc}\sqrt{{\lambda }_1}& 0\\ 0& \sqrt{{\lambda }_2}\end{array}\right]$=$\left[\begin{array}{cc}0.707& 0\\ -0.316& 0.899\\ 0.632& 0.447\end{array}\right]$$\left[\begin{array}{cc}\sqrt{1.754}& 0\\ 0& \sqrt{1}\end{array}\right]$=$\left[\begin{array}{cc}0.936& 0\\ -0.419& 0.899\\ 0.837& 0.447\end{array}\right]$
STEP2由A可以建立因子模型：
$X_1$=0.936$F_1$+${\epsilon }_1$
$X_2$=-0.419$F_1$+0.899$F_2$+${\epsilon }_2$
$X_3$=0.837$F_1$+0.447$F_2$+${\epsilon }_3$

（2）共同度即对A的行求平方和，则：
$h_1^2$=0.936²+0²=0.876
$h_2^2$=0.419²+0.899²=0.984
$h_3^2$=0.837²+0.447²=0.9

（3）公共因子对X的贡献即对A的列求平方和，由于是从约相关阵计算的特征值，所以$q_1^2$=${\lambda }_1$=1.754

例二

设某总体可用 3 个指标来描述，在因子分析时，从约相关阵出发计算出特征值为${\lambda }_1$=1.96，${\lambda }_2$=1，${\lambda }_3$=0.25。又知${\lambda }_1$，${\lambda }_2$，${\lambda }_3$对应的单位特征向量分别为(0.707，-0.316，0.632) ’,
(0，0.899，0.447) ’及(0.929，-0.261，0.261)’，要求：
（1）计算因子载荷矩阵A，并建立因子模型。
（2）计算共同度$h_i$²（i=1，2，3）。
（3）计算第一公共因子对总体的贡献。

---

这题和上一题一样，只不过需要我们自己确定公共因子的个数
解：
（1）根据题意，（${\lambda }_1$+${\lambda }_2$）/（${\lambda }_1$+${\lambda }_2$+${\lambda }_3$）= 92%，因此我们选择前两个特征值所对应的公共因子即可。

STEP1A=($u_1$，$u_2$) $\left[\begin{array}{cc}\sqrt{{\lambda }_1}& 0\\ 0& \sqrt{{\lambda }_2}\end{array}\right]$=$\left[\begin{array}{cc}0.707& 0\\ -0.316& 0.899\\ 0.632& 0.447\end{array}\right]$$\left[\begin{array}{cc}\sqrt{1.96}& 0\\ 0& \sqrt{1}\end{array}\right]$=$\left[\begin{array}{cc}0.99& 0\\ -0.442& 0.899\\ 0.885& 0.447\end{array}\right]$
STEP2由此可以建立因子模型：

$X_1$=0.99$F_1$+${\epsilon }_1$
$X_2$=-0.442$F_1$+0.899$F_2$+${\epsilon }_2$
$X_3$=0.885$F_1$+0.447$F_2$+${\epsilon }_3$

（2）共同度即对A的行求平方和，则：

$h_1^2$=0.9898²+0²=0.98
$h_2^2$=0.442²+0.899²=1.004
$h_3^2$=0.885²+0.447²=0.983

（3）公共因子对X的贡献即对A的列求平方和，由于是从约相关阵计算的特征值，所以$q_1^2$=${\lambda }_1$=1.96

例三

【应用多元统计分析（高惠璇版）习题8-1】

设标准化变量$X_1$，$X_2$，$X_3$的协方差阵(即相关阵)为
$$R=\left[\begin{array}{ccc}1.00& 0.63& 0.45\\ 0.63& 1.00& 0.35\\ 0.45& 0.35& 1.00\end{array}\right]$$
试求m=1的正交因子模型.

---

解：
求正交因子模型，转换为求因子载荷矩阵A，m=1时，只需要求A的第一列$a_1$即可。

由主因子法我们知道R=AA'+D

R=$\left[\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\end{array}\right]$[$a_{11}$，$a_{21}$，$a_{31}$] +$\left[\begin{array}{ccc}{\sigma }_1^2& 0& 0\\ 0& {\sigma }_2^2& 0\\ 0& 0& {\sigma }_3^2\end{array}\right]$

所以可得以下方程:
$a_{11}^2$+ ${\sigma }_1^2$ = 1
$a_{21}^2$+ ${\sigma }_2^2$ = 1
$a_{31}^2$+ ${\sigma }_3^2$ = 1
$a_{11}$ $a_{21}$=0.63
$a_{11}$ $a_{31}$=0.45
$a_{31}$ $a_{21}$=0.35

由此可解得：$a_{11}$=0.5， $a_{21}$=0.7，$a_{31}$=0.9

${\sigma }_1^2$=1 - $a_{11}^2$=1-0.81=0.19
${\sigma }_2^2$=1 - $a_{21}^2$=1-0.49=0.51
${\sigma }_3^2$=1 - $a_{31}^2$=1-0.25=0.75

所以，m=1时，A=$\left[\begin{array}{c}0.5\\ 0.7\\ 0.9\end{array}\right]$

正交因子模型为：

$X_1$=0.9$F_1$+${\epsilon }_1$
$X_2$=0.7$F_1$+${\epsilon }_2$
$X_3$=0.5$F_1$+${\epsilon }_3$

特殊因子ε的协方差阵D为

$D=\left[\begin{array}{ccc}0.19& 0& 0\\ 0& 0.51& 0\\ 0& 0& 0.75\end{array}\right]$

例四

【应用多元统计分析（高惠璇版）习题8-2】
已知题8-1中R的特征值和特征向量分别为
（1）取公共因子个数m=1时，求因子模型的主成分解，并计算误差平方和Q(1)；
（2）取公共因子个数m=2时，求因子模型的主成分解，并计算误差平方和Q(2)；
（3）试求误差平方和Q(m)<0.1的主成分解。

---

解：
（1）m=1时，A=$\sqrt{{\lambda }_1}$$l_1$=
$\left[\begin{array}{c}{a}_{11}\\ a_{21}\\ a_{31}\end{array}\right]$=$\left[\begin{array}{c}0.8757\\ 0.8312\\ 0.7111\end{array}\right]$

因子模型为：

$X_1$=0.8757$F_1$+${\epsilon }_1$
$X_2$=0.8312$F_1$+${\epsilon }_2$
$X_3$=0.7111$F_1$+${\epsilon }_3$

则：
${\sigma }_1^2$=1 - $a_{11}^2$=1-0.8757²=0.2331
${\sigma }_2^2$=1 - $a_{21}^2$=1-0.8312²=0.3091
${\sigma }_3^2$=1 - $a_{31}^2$=1-7111²=0.4943
所以：
D=$\left[\begin{array}{ccc}0.2331& 0& 0\\ 0& 0.3091& 0\\ 0& 0& 0.4943\end{array}\right]$

可算出残差矩阵$E=R-AA’-D$ ，由上一题我们知道R=$\left[\begin{array}{ccc}1.00& 0.63& 0.45\\ 0.63& 1.00& 0.35\\ 0.45& 0.35& 1.00\end{array}\right]$，A和D我们都已经算出来，所以E=$\left[\begin{array}{ccc}0& -0.098& -0.173\\ & 0& -0.241\\ & & 0\end{array}\right]$

所以Q(1)=2x(0.098²+0.173²+0.241²)=0.195

（2）m=2时，A=($l_1$，$l_2$) $\left[\begin{array}{cc}\sqrt{{\lambda }_1}& 0\\ 0& \sqrt{{\lambda }_2}\end{array}\right]$=$\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\\ a_{31}& a_{32}\end{array}\right]$=$\left[\begin{array}{cc}0.8757& -0.1802\\ 0.8312& -0.4048\\ 0.7111& 0.6950\end{array}\right]$

因子模型为
$X_1$=0.8757$F_1$-0.1802$F_2$+${\epsilon }_1$
$X_2$=0.8312$F_1$-0.4048$F_2$+${\epsilon }_2$
$X_3$=0.7111$F_1$+0.695$F_2$+${\epsilon }_3$

同理我们可以计算出D= $\left[\begin{array}{ccc}0.2007& 0& 0\\ 0& 0.1452& 0\\ 0& 0& 0.0113\end{array}\right]$、E= $\left[\begin{array}{ccc}0& -0.1708& -0.0475\\ & 0& 0.0403\\ & & 0\end{array}\right]$

所以Q(2)=2x(0.1708²+0.0475²+0.0403²)=0.0661

（3）由（2）我们知道Q(2)<0.1，故m=2的主成分解满足要求。