3.1 数据结构分类
常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图,它们可以从“逻辑结构”和“物理结构”两个维度进行分类。
3.1.1逻辑结构:线性与非线性
逻辑结构揭示了数据元素之间的逻辑关系。在数组和链表中,数据按照顺序依次排列,体现了数据之间的线性关系;而在树中,数据从顶部向下按层次排列,表现出祖先与后代之间的派生关系;图则由节点和边构成,反映了复杂的网络关系。
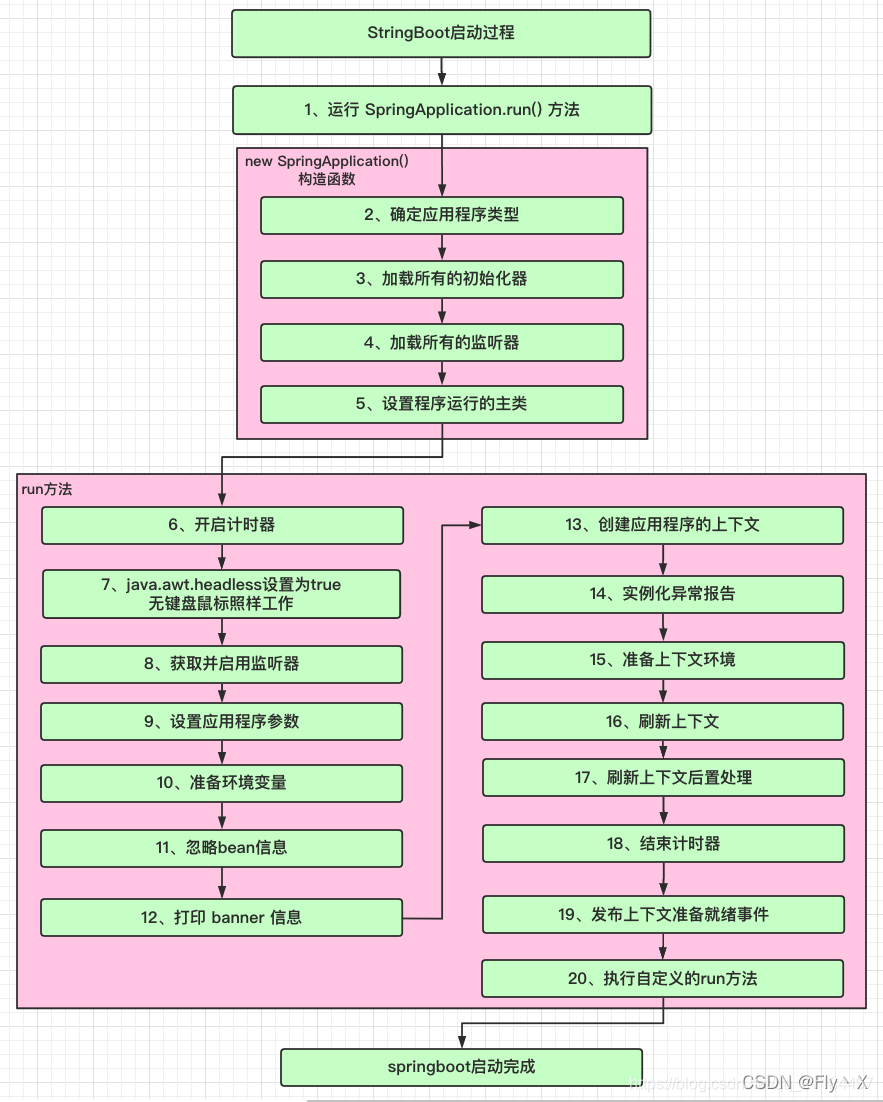
如下图所示,逻辑结构可被分为“线性”和“非线性”两大类。线性结构比较直观,指数据在逻辑关系上呈线性排列;非线性结构则相反,呈非线性排列。
- 线性数据结构:数组、链表、栈、队列、哈希表。
- 非线性数据结构:树、堆、图、哈希表。
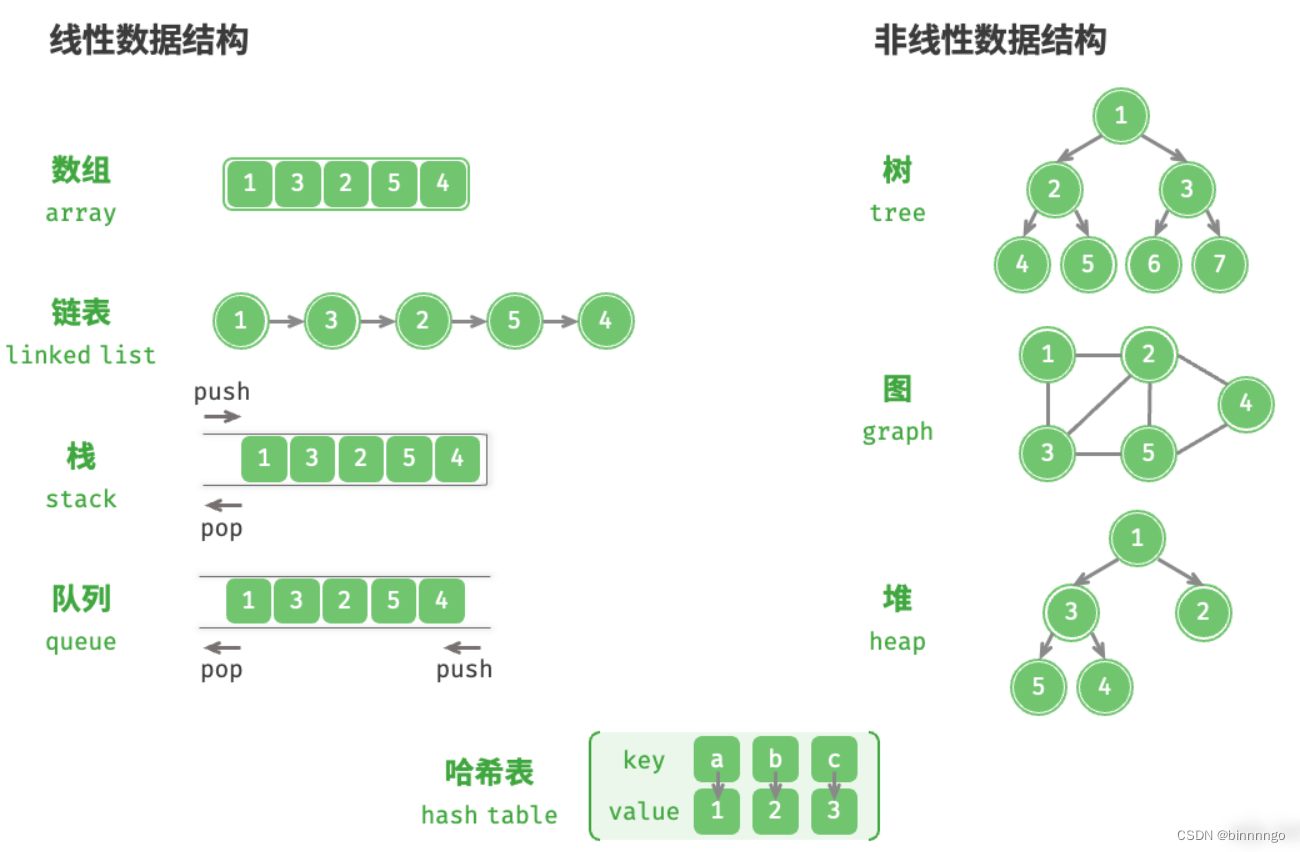
非线性数据结构可以进一步被划分为树形结构和网状结构。
- 线性结构:数组、链表、队列、栈、哈希表,元素之间是一对一的顺序关系。
- 树形结构:树、堆、哈希表,元素之间是一对多的关系。
- 网状结构:图,元素之间是多对多的关系。
3.1.2 物理结构:连续与分散
当算法程序运行时,正在处理的数据主要被存储在内存中。下图展示了一个计算机内存条,其中每个黑色方块都包含一块内存空间。我们可以将内存想象成一个巨大的 Excel 表格,其中每个单元格都可以存储一定大小的数据。系统通过内存地址来访问目标位置的数据。如下图所示,计算机根据特定规则为表格中的每个单元格分配编号,确保每个内存空间都有唯一的内存地址。有了这些地址,程序便可以访问内存中的数据。
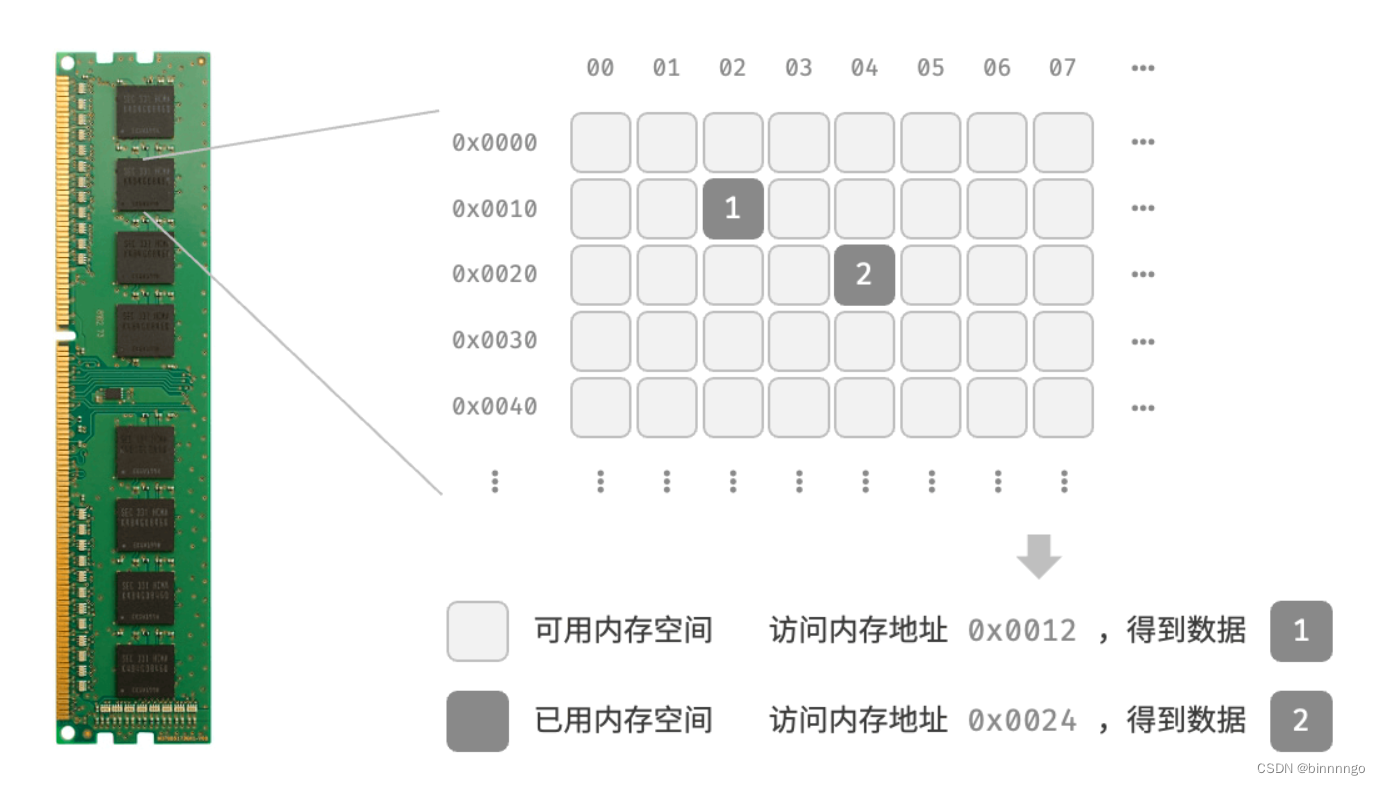
内存是所有程序的共享资源,当某块内存被某个程序占用时,则无法被其他程序同时使用了。因此在数据结构与算法的设计中,内存资源是一个重要的考虑因素。比如,算法所占用的内存峰值不应超过系统剩余空闲内存;如果缺少连续大块的内存空间,那么所选用的数据结构必须能够存储在分散的内存空间内。
如下图所示,物理结构反映了数据在计算机内存中的存储方式,可分为连续空间存储(数组)和分散空间存储(链表)。物理结构从底层决定了数据的访问、更新、增删等操作方法,在时间效率和空间效率方面呈现出互补的特点。
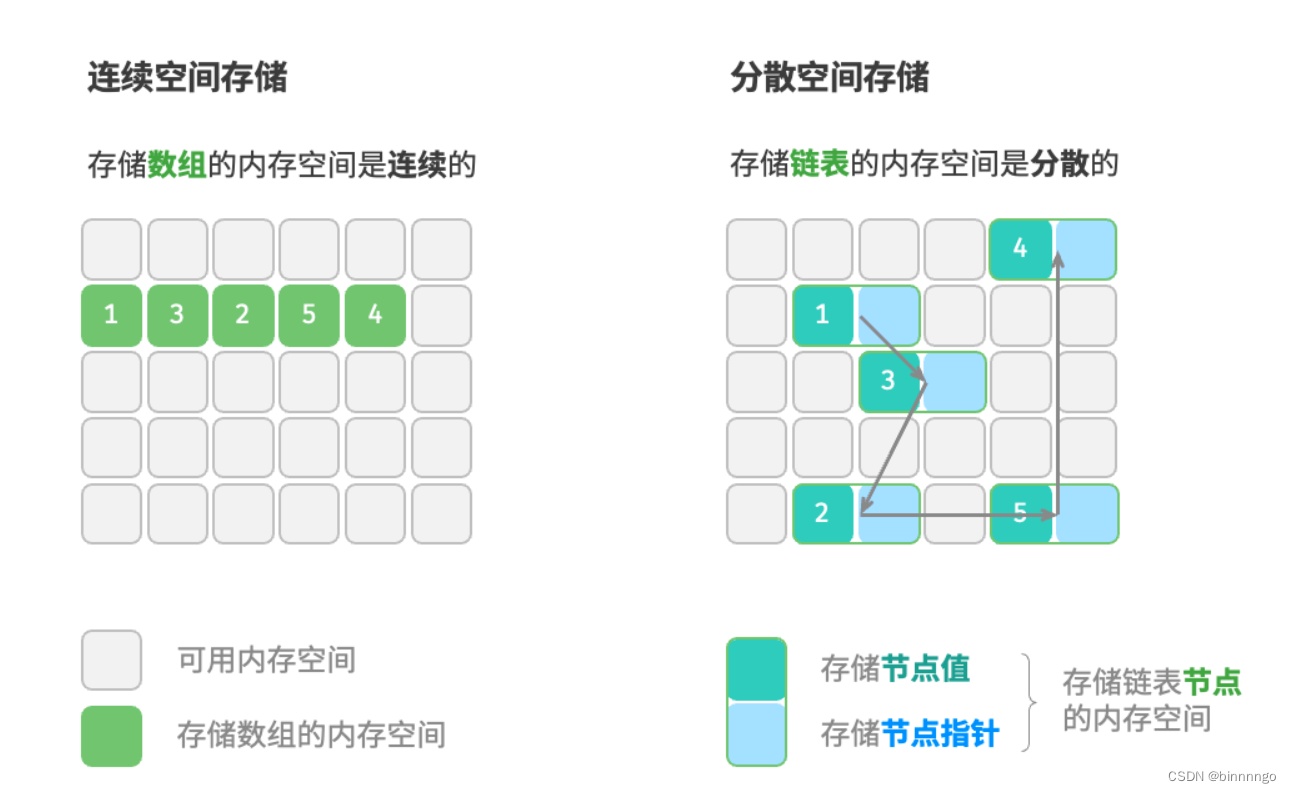
值得说明的是,所有数据结构都是基于数组、链表或二者的组合实现的。例如,栈和队列既可以使用数组实现,也可以使用链表实现;而哈希表的实现可能同时包含数组和链表。
- 基于数组可实现:栈、队列、哈希表、树、堆、图、矩阵、张量(维度 ≥3 的数组)等。
- 基于链表可实现:栈、队列、哈希表、树、堆、图等。
基于数组实现的数据结构也被称为“静态数据结构”,这意味着此类数据结构在初始化后长度不可变。相对应地,基于链表实现的数据结构被称为“动态数据结构”,这类数据结构在初始化后,仍可以在程序运行过程中对其长度进行调整。
3.2 基本数据类型
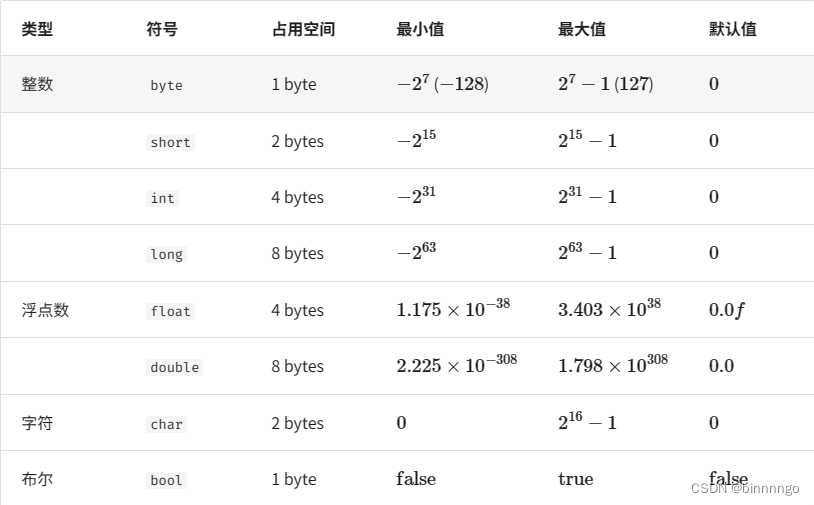
基本数据类型是 CPU 可以直接进行运算的类型,在算法中直接被使用,主要包括以下几种类型。
1.整型(Integer): 整型用于表示整数值。有几种不同大小的整型可供选择,包括:
- int: 通常是最常用的整型,占用4个字节,范围约为-2,147,483,648到2,147,483,647。
- short: 占用2个字节,范围约为-32,768到32,767。
- long: 占用4个字节或8个字节,范围较大,至少与int相同。
- long long: 占用8个字节,范围更大,至少与long相同。
2.浮点型(Floating-point): 浮点型用于表示带有小数部分的数值。有两种常见的浮点型:
- float: 单精度浮点数,占用4个字节。
- double: 双精度浮点数,占用8个字节。
3.字符型(Character): 字符型用于表示单个字符。
4.布尔型(Boolean): 布尔型用于表示逻辑值,只有两个可能的取值:true和false。
基本数据类型与数据结构之间有什么联系呢?我们知道,数据结构是在计算机中组织与存储数据的方式。它的主语是“结构”而非“数据”。
如果想要表示“一排数字”,我们自然会想到使用数组。这是因为数组的线性结构可以表示数字的相邻关系和顺序关系,但至于存储的内容是整数 int、小数 float 或是字符 char ,则与“数据结构”无关。
换句话说,基本数据类型提供了数据的“内容类型”,而数据结构提供了数据的“组织方式”。例如以下代码,我们用相同的数据结构(数组)来存储与表示不同的基本数据类型,包括 int、float、char、bool 等。
换句话说,基本数据类型提供了数据的“内容类型”,而数据结构提供了数据的“组织方式”。例如以下代码,我们用相同的数据结构(数组)来存储与表示不同的基本数据类型。
// 使用多种基本数据类型来初始化数组
int numbers[5];
float decimals[5];
char characters[5];
bool bools[5];